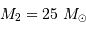Crédit :
ESO
Séparation
L'observation des étoiles binaires visuelles est limitée par la qualité d'image des observations au sol. La plus petite séparation angulaire détectable depuis le sol est d'environ 1 seconde d'arc. Cette limite imposée par la turbulence atmosphérique est améliorée grâce à l'optique adaptative. L'interférométrie sur les VLT permet d'atteindre une séparation de quelques millièmes de seconde d'arc.
Sélection
L'effet de sélection dans l'observation de ces couples est très important. Deux catégories d'objets sont en particulier très difficile à observer : les binaires à longue période d'une part, et d'autre part les étoiles qui forment au contraire un système très serré.
La séparation caractéristique de tels couples varie d'une fraction d'unité astronomique à quelques centaines d'unités astronomiques, quand leurs périodes s'échelonnent de quelques années à plus d'un siècle. Les périodes plus longues (quelques siècles) ou les orbites plus grandes sont très difficiles à mettre en évidence, essentiellement pour des raisons de recul dans le temps.
 Binaire visuelle
Binaire visuelle
Difficulté : ☆
Temps : 30 min
On observe une étoile double visuelle dont les caractéristiques observées sont les suivantes :
| séparation angulaire maximum | 5" |
| séparation angulaire minimum | 1" |
parallaxe 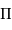 | 0.1" |
période de révolution 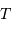 | 30 ans |
L'étoile primaire 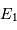 se trouve au foyer de l'orbite observée ; le compagnon est observé à une distance du barycentre 5 fois plus grande que celle de l'étoile primaire.
se trouve au foyer de l'orbite observée ; le compagnon est observé à une distance du barycentre 5 fois plus grande que celle de l'étoile primaire.
Question 1)
Montrer que l'inclinaison  du plan de l'orbite est nulle.
du plan de l'orbite est nulle.
Question 2)
Déterminer le rapport des masses des deux étoiles.
Question 3)
Exprimer la loi du mouvement des deux corps (troisième loi de Kepler) en prenant comme unités de masse, la masse du Soleil, de temps, l'année, et de distance, la distance Terre-Soleil (unité astronomique).
Question 4)
Calculer la distance en parsec à partir de la parallaxe, puis le demi-grand axe en UA.
Question 5)
Déterminer la masse de chaque composante en unité de masse solaire.
- Question 1
Solution :
On appelle 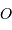 le centre de l'ellipse observée et A l'intersection de la demi-droite [0E) avec l'ellipse. Comme l'excentricité
le centre de l'ellipse observée et A l'intersection de la demi-droite [0E) avec l'ellipse. Comme l'excentricité 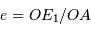 est invariante par projection, le fait que l'étoile primaire soit au foyer de l'orbite projetée montre que le grand axe de l'orbite projetée correspond à la projection du grand axe, ce qui ne peut avoir lieu que si
est invariante par projection, le fait que l'étoile primaire soit au foyer de l'orbite projetée montre que le grand axe de l'orbite projetée correspond à la projection du grand axe, ce qui ne peut avoir lieu que si 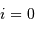 ...
...
- Question 2
Solution :
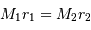 et
et 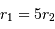 implique un rapport de masse
implique un rapport de masse 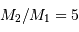
- Question 3
Solution :
La troisième loi de Kepler, en unités, UA, année, masse solaire, s'exprime :
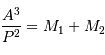
- Question 4
Solution :
La parallaxe étant de 0.1", le système double est situé à 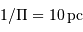 de nous et qu'une unité astronomique y est vue sous un angle de 0,1".
de nous et qu'une unité astronomique y est vue sous un angle de 0,1".
Le demi-grand axe apparent est égal à 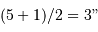 ; le demi-grand axe est donc de 30 UA.
; le demi-grand axe est donc de 30 UA.
- Question 5
Solution :
On applique la troisième loi de Kepler pour calculer la somme des masses :
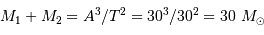 .
.
et on obtient 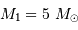 et
et 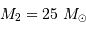

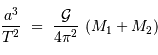
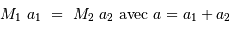
 représente le demi-grand axe de l'orbite relative du corps de masse
représente le demi-grand axe de l'orbite relative du corps de masse  par rapport au corps de masse
par rapport au corps de masse 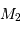 et
et 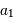 et
et 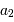 sont les demi-grands axes des orbites absolues de chacun des corps par rapport au barycentre
sont les demi-grands axes des orbites absolues de chacun des corps par rapport au barycentre 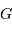 du système.
du système.
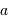 ,
, 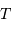 et de la position du barycentre du système (c'est-à-dire des demi-grands axes
et de la position du barycentre du système (c'est-à-dire des demi-grands axes 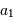 et
et 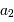 ) permet alors de déterminer
) permet alors de déterminer 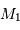 et
et 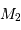 .
.
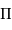
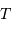
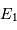 se trouve au foyer de l'orbite observée ; le compagnon est observé à une distance du barycentre 5 fois plus grande que celle de l'étoile primaire.
se trouve au foyer de l'orbite observée ; le compagnon est observé à une distance du barycentre 5 fois plus grande que celle de l'étoile primaire.
 du plan de l'orbite est nulle.
du plan de l'orbite est nulle.
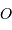 le centre de l'ellipse observée et A l'intersection de la demi-droite [0E) avec l'ellipse. Comme l'excentricité
le centre de l'ellipse observée et A l'intersection de la demi-droite [0E) avec l'ellipse. Comme l'excentricité 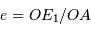 est invariante par projection, le fait que l'étoile primaire soit au foyer de l'orbite projetée montre que le grand axe de l'orbite projetée correspond à la projection du grand axe, ce qui ne peut avoir lieu que si
est invariante par projection, le fait que l'étoile primaire soit au foyer de l'orbite projetée montre que le grand axe de l'orbite projetée correspond à la projection du grand axe, ce qui ne peut avoir lieu que si 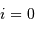 ...
...
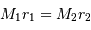 et
et 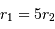 implique un rapport de masse
implique un rapport de masse 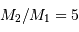
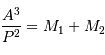
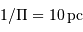 de nous et qu'une unité astronomique y est vue sous un angle de 0,1".
de nous et qu'une unité astronomique y est vue sous un angle de 0,1".
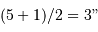 ; le demi-grand axe est donc de 30 UA.
; le demi-grand axe est donc de 30 UA.
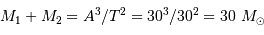 .
.
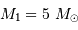 et
et