
|
La 3ème loi de Kepler porte en elle, comme toute loi physique, une potentialité énorme : généraliser le particulier, pour mieux comprendre comment fonctionne l'univers.
Il se trouve que sur ce point de vue, elle fonctionne extraordinairement bien. Elle permet de "peser" tout objet de l'Univers, à la seule condition qu'un objet moins massif tourne autour de lui.
Trajectoires elliptiques
Peser est à prendre ici non dans son sens physique (mesurer le poids), mais dans son sens de la vie courante : mesurer la masse. La mécanique newtonienne permet de préciser la constante intervenant dans la 3ème loi de Kepler appliquée à un système ressemblant au système solaire : un ou des objets peu massifs tournant dans le potentiel central d'un corps plus massif.
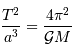
Cette loi implique 3 paramètres physiques : la période 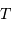 de révolution
et le demi-grand axe de l'orbite, et la masse
de révolution
et le demi-grand axe de l'orbite, et la masse 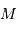 du corps central.
du corps central.
La mesure de 2 parmi ces 3 paramètres permet d'en déduire le 3ème : ceci
est mis à profit pour déterminer la masse 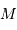 du centre de force à
partir des paramètres orbitaux
du centre de force à
partir des paramètres orbitaux 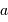 et
et 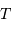 . Ces 2 termes sont en effet
observables, alors que la masse ne l'est pas.
. Ces 2 termes sont en effet
observables, alors que la masse ne l'est pas.
La mesure de la période 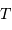 nécessite de repérer le mouvement le long de
la trajectoire.
nécessite de repérer le mouvement le long de
la trajectoire.
La mesure du demi-grand axe de l'orbite découle de la mesure de sa taille angulaire, et nécessite de connaître la distance du système. On voit une fois encore l'importance de la mesure des distances en astronomie.
| Planète | 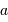 | 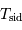 |  | 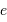 | 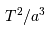 |
| UA | an | deg | 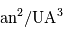 | ||
| Mercure | 0.3871 | 0.2408 | 7.0 | 0.206 | 0.9996 |
| Vénus | 0.7233 | 0.6152 | 3.4 | 0.007 | 1.0002 |
| Terre | 1.0000 | 1.0000 | -- | 0.017 | 1 |
| Mars | 1.5237 | 1.8808 | 1.8 | 0.093 | 1.0000 |
| Jupiter | 5.2026 | 11.862 | 1.3 | 0.048 | 0.9992 |
| Saturne | 9.5547 | 29.457 | 2.5 | 0.056 | 0.9948 |
| Uranus | 19.218 | 84.020 | 0.8 | 0.046 | 0.9946 |
| Neptune | 30.109 | 164.77 | 1.8 | 0.009 | 0.9946 |
Indépendamment de l'inclinaison  sur l'écliptique et de l'excentricité
sur l'écliptique et de l'excentricité
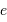 de l'orbite de chacune des 8 planètes, la relation
de l'orbite de chacune des 8 planètes, la relation 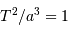 est vérifiée, avec
est vérifiée, avec 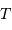 la période de révolution sidérale.
Les désaccords proviennent des écarts aux hypothèses de Kepler.
Remarque : dans le système solaire, les masses des planètes et de la
plupart de leurs satellites sont connues avec une précision relative de
l'ordre de
la période de révolution sidérale.
Les désaccords proviennent des écarts aux hypothèses de Kepler.
Remarque : dans le système solaire, les masses des planètes et de la
plupart de leurs satellites sont connues avec une précision relative de
l'ordre de 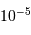 . Il s'agit de la précision à laquelle est mesurée
la constante gravitationnelle
. Il s'agit de la précision à laquelle est mesurée
la constante gravitationnelle 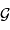 . Le produit
. Le produit 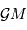 est souvent
déterminé avec une précision bien meilleure.
est souvent
déterminé avec une précision bien meilleure.
Lorsque l'on choisit le système d'unités où les temps se comptent en année, les distances en unité astronomique, et les masses en masse solaire, la 3ème loi de Kepler se réécrit, pour le système solaire.
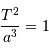
Sans mener aucun calcul, il suffit pour s'en convaince d'examiner le cas de l'orbite terrestre, pour lequel 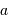 = 1 UA,
= 1 UA, 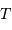 = 1 an, qui valide le cas de tout autre planète.
= 1 an, qui valide le cas de tout autre planète.
Pour un autre système caractérisé par un centre de force de masse 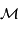 ,
la 3ème loi devient, toujours dans le système d'unités (UA, an,
,
la 3ème loi devient, toujours dans le système d'unités (UA, an,
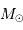 ) :
) :
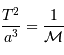
Une application de cette loi sur différents exemples illustre comment une loi physique peut étendre sa validité sur une très large gamme de valeurs.