Systèmes doubles
L'astéroide Eugénie et son satellite
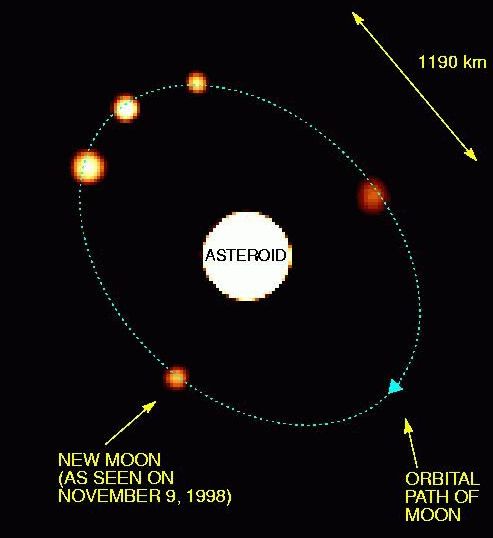
Superposition d'images obtenues
par optique adaptative au télescope
CFH (Merline, 1998). La détermination des paramètres
orbitaux du satellite -- période de rotation et demi-grand axe -- permet
de mesurer la masse de l'astéroïde
(
exercice).
La période est 4.7 jours, le demi-grand axe 1190 km.
Crédit :
CFHT
Le mouvement d'Eugénie

Le satellite de l'astéroïde Eugénie, observé en optique adaptative :
film obtenu avec 5 poses à 5 dates différentes
Crédit :
CFHT
Sirius A et B
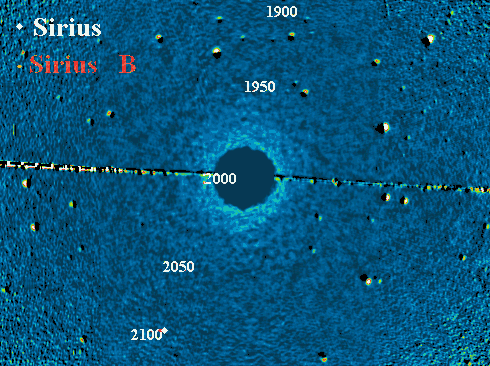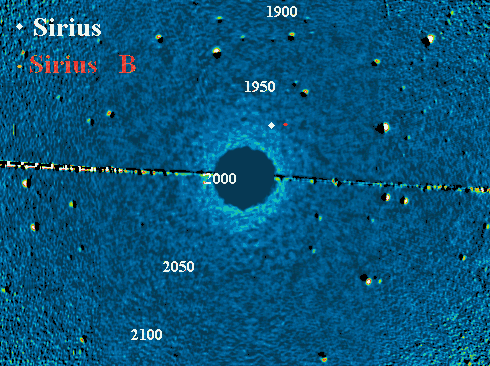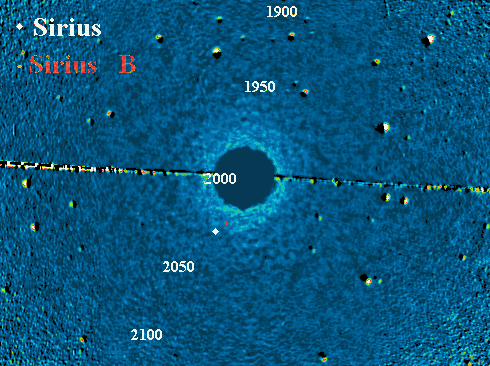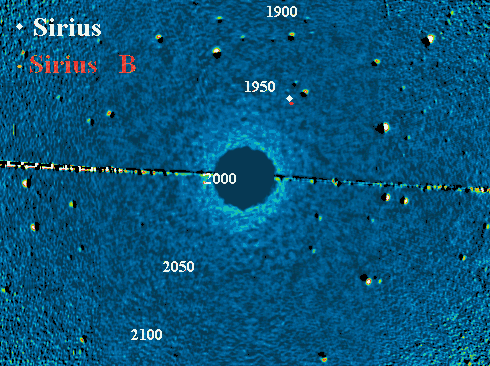
Animation des orbites de Sirius A et B (respectivement les points blanc et
rouge), sur fond d'étoiles fixes. Au mouvement apparent du système se superpose
la rotation du système.
Crédit :
Observatoire du Pic du Midi
L'observation des systèmes doubles est cruciale en astronomie, car elle donne accès à la mesure de la masse du système. On en voit deux exemples, à des échelles différentes :
 Objectifs
Objectifs
La 3ème loi de Kepler porte en elle, comme toute loi physique, une
potentialité énorme : généraliser le particulier, pour mieux comprendre
comment fonctionne l'univers.
Il se trouve que sur ce point de vue, elle fonctionne extraordinairement
bien. Elle permet de "peser" tout objet de l'Univers, à la seule
condition qu'un objet moins massif tourne autour de lui.
Déterminer la masse du centre de force
Peser est à prendre ici non dans son sens physique (mesurer le poids),
mais dans son sens de la vie courante : mesurer la masse.
La mécanique newtonienne permet de préciser la constante intervenant
dans la 3ème loi de Kepler appliquée à un système ressemblant au système
solaire : un ou des objets peu massifs tournant dans le potentiel
central d'un corps plus massif.
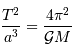
Cette loi implique 3 paramètres physiques : la période 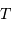 de révolution
et le demi-grand axe de l'orbite, et la masse
de révolution
et le demi-grand axe de l'orbite, et la masse 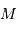 du corps central.
du corps central.
La mesure de 2 parmi ces 3 paramètres permet d'en déduire le 3ème : ceci
est mis à profit pour déterminer la masse 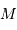 du centre de force à
partir des paramètres orbitaux
du centre de force à
partir des paramètres orbitaux 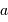 et
et 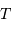 . Ces 2 termes sont en effet
observables, alors que la masse ne l'est pas.
. Ces 2 termes sont en effet
observables, alors que la masse ne l'est pas.
La mesure de la période 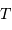 nécessite de repérer le mouvement le long de
la trajectoire.
nécessite de repérer le mouvement le long de
la trajectoire.
La mesure du demi-grand axe de l'orbite découle de la mesure de sa
taille angulaire, et nécessite de connaître la distance du système.
On voit une fois encore l'importance de la mesure des distances en
astronomie.
La 3ème loi de Kepler appliquée au système solaire
| Planète | 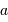 | 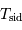 |  | 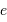 | 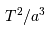 |
| UA | an | deg | | 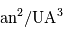 |
| Mercure | 0.3871 | 0.2408 | 7.0 | 0.206 | 0.9996 |
| Vénus | 0.7233 | 0.6152 | 3.4 | 0.007 | 1.0002 |
| Terre | 1.0000 | 1.0000 | -- | 0.017 | 1 |
| Mars | 1.5237 | 1.8808 | 1.8 | 0.093 | 1.0000 |
| Jupiter | 5.2026 | 11.862 | 1.3 | 0.048 | 0.9992 |
| Saturne | 9.5547 | 29.457 | 2.5 | 0.056 | 0.9948 |
| Uranus | 19.218 | 84.020 | 0.8 | 0.046 | 0.9946 |
| Neptune | 30.109 | 164.77 | 1.8 | 0.009 | 0.9946 |
Indépendamment de l'inclinaison  sur l'écliptique et de l'excentricité
sur l'écliptique et de l'excentricité
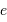 de l'orbite de chacune des 8 planètes, la relation
de l'orbite de chacune des 8 planètes, la relation 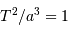 est vérifiée, avec
est vérifiée, avec 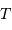 la période de révolution sidérale.
Les désaccords proviennent des écarts aux hypothèses de Kepler.
Remarque : dans le système solaire, les masses des planètes et de la
plupart de leurs satellites sont connues avec une précision relative de
l'ordre de
la période de révolution sidérale.
Les désaccords proviennent des écarts aux hypothèses de Kepler.
Remarque : dans le système solaire, les masses des planètes et de la
plupart de leurs satellites sont connues avec une précision relative de
l'ordre de 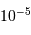 . Il s'agit de la précision à laquelle est mesurée
la constante gravitationnelle
. Il s'agit de la précision à laquelle est mesurée
la constante gravitationnelle 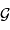 . Le produit
. Le produit 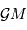 est souvent
déterminé avec une précision bien meilleure.
est souvent
déterminé avec une précision bien meilleure.
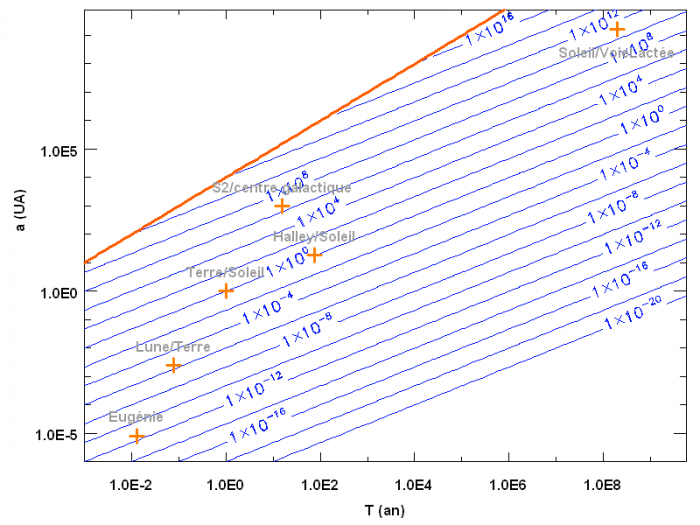
Lignes isomasses de la masse (en unité de masse solaire) du centre force dérivée de la mesure des paramètres orbitaux de différents systèmes. La limite en rouge est relativiste : la vitesse orbitale ne peut pas dépasser la vitesse de la lumière. Les différents systèmes représentés illustrent la diversité de la gamme d'application des lois de la gravitation.
Crédit :
ASM
Différents systèmes d'unités
Lorsque l'on choisit le système d'unités où les temps se comptent en année, les distances en unité astronomique, et les masses en masse solaire, la 3ème loi de Kepler se réécrit, pour le système solaire.
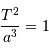
Sans mener aucun calcul, il suffit pour s'en convaince d'examiner le cas de l'orbite terrestre, pour lequel 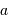 = 1 UA,
= 1 UA, 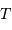 = 1 an, qui valide le cas de tout autre planète.
= 1 an, qui valide le cas de tout autre planète.
Pour un autre système caractérisé par un centre de force de masse 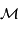 ,
la 3ème loi devient, toujours dans le système d'unités (UA, an,
,
la 3ème loi devient, toujours dans le système d'unités (UA, an,
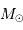 ) :
) :
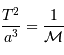
Une application de cette loi sur différents exemples illustre comment une loi physique peut étendre sa validité sur une très large gamme de valeurs.
 Peser un astéroide
Peser un astéroide
Difficulté : ☆
Temps : 15 min
Une équipe dirigée par W. Merline a observé en 1998 l'astéroïde
(45)Eugénie avec l'optique adaptative du télescope CFH. Les
observations
ont mis en évidence la présence d'un petit satellite.
Paramètres orbitaux
| Période | 4.7 j |
| Demi-grand axe | 1190 km |
| Diamètre de Eugénie | 215 km |
| Diamètre du satellite | 13 km |
Question 1)
Déterminer la masse de (45)Eugénie
Il s'agit d'une application de la 3ème loi de Kepler. On rappelle 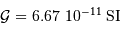
Question 2)
En déduire la masse volumique moyenne de Eugénie. Estimer sa
composition.
On suppose une forme sphérique de rayon 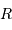 , de volume
, de volume 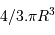
Question 3)
Peut-on estimer la masse du petit satellite ?
Une hypothèse sur la masse volumique du petit satellite est nécessaire.
 Peser la Voie Lactée
Peser la Voie Lactée
Difficulté : ☆☆
Temps : 20 min
Notre galaxie, la Voie Lactée, a la forme d'une galette d'environ 30000 pc de diamètre et 2000 pc d'épaisseur. La région centrale est
formée d'un bulbe d'allure sphérique de 2 700 pc de rayon, qui
contient l'essentiel de la masse galactique.
Le Soleil orbite à 8000 pc du centre galactique.
D'après les mesures Doppler effectuées sur la raie à 21 cm de l'hydrogène,
l'orbite du Soleil est approximativement circulaire, et la vitesse
orbitale du Soleil est d'environ  .
.
Question 1)
Déterminer la période 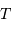 du mouvement du soleil autour du centre
galactique. L'exprimer en années.
du mouvement du soleil autour du centre
galactique. L'exprimer en années.
Commencer par déterminer le rayon 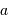 de la trajectoire du soleil autour du centre galactique, avec
de la trajectoire du soleil autour du centre galactique, avec
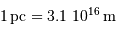 .
.
Question 2)
Estimer la masse du bulbe galactique,
en unité de masse solaire 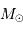 .
.
Mener le calcul en unités UA, an et 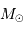 , avec
, avec
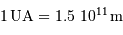 .
.
 La 3ème loi de Kepler pour une orbite circulaire
La 3ème loi de Kepler pour une orbite circulaire
Difficulté : ☆
Temps : 20 min
Question 1)
Retrouver l'expression de la 3ème loi
de Kepler d'après le cas particulier d'une orbite circulaire, lorsque
l'on suppose que les masses des 2 objets vérifient 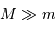 .
.
[1 points]
Définir convenablement un système, et faire un bilan de force
Exprimer l'accélération radiale en fonction de la vitesse 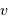 et du rayon de
courbure
et du rayon de
courbure 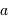 de la trajectoire.
de la trajectoire.
Relier la vitesse orbitale au rayon 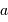 et à la période orbitale
et à la période orbitale 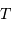 .
.
 Comète de Halley
Comète de Halley
Difficulté : ☆
Temps : 20 min
Question 1)
La comète de Halley a une période sidérale de 76 années. En déduire le
demi-grand axe de son orbite.
[1 points]
Traiter le calcul directement en UA et années
En UA et années; 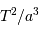 = 1 dans le système solaire
= 1 dans le système solaire
Question 2)
L'excentricité de son orbite vaut 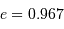 , Déterminer son aphélie
, Déterminer son aphélie 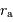 , son
périhélie
, son
périhélie 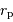 . Situer ces distances par rapport aux autres planètes.
. Situer ces distances par rapport aux autres planètes.
[1 points]
Le lien entre demi-grand axe, excentricité, périhélie et aphélie s'exprime
par :
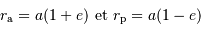
- Question 1
Aide :
Il s'agit d'une application de la 3ème loi de Kepler. On rappelle 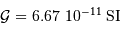
Solution :
Le calcul en unités SI avec les données:
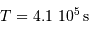 ,
, 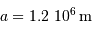 , et la constante gravitationnelle
, et la constante gravitationnelle 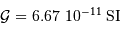 ,
,
aboutit par application de la 3e loi de Kepler à :
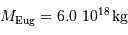
- Question 2
Aide :
On suppose une forme sphérique de rayon 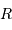 , de volume
, de volume 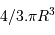
Solution :
La masse volumique s'écrit : 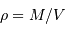 ,
,
avec le volume
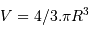 , on trouve :
, on trouve :
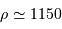 kg.m
kg.m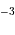 .
.
L'astéroïde (45)Eugénie semble peu dense, avec vraisemblablement un empilement lacunaire de roches.
- Question 3
Aide :
Une hypothèse sur la masse volumique du petit satellite est nécessaire.
Solution :
C'est impossible par la 3ème loi de Kepler. Une estimation, supposant
une masse volumique moyenne identique à celle de Eugénie, conduit à une
masse dans le rapport du cube des rayons :
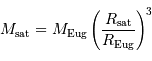
D'où : 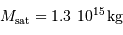 .
On peut vérifier, a posteriori et dans le cadre de l'hypothèse posée, que cette masse est très petite devant la masse du satellite principale, et que donc la 3ème loi de Kepler s'applique bien pour déterminer la masse d'Eugénie (cf. question 1).
.
On peut vérifier, a posteriori et dans le cadre de l'hypothèse posée, que cette masse est très petite devant la masse du satellite principale, et que donc la 3ème loi de Kepler s'applique bien pour déterminer la masse d'Eugénie (cf. question 1).



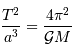
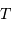 de révolution
et le demi-grand axe de l'orbite, et la masse
de révolution
et le demi-grand axe de l'orbite, et la masse 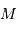 du corps central.
du corps central.
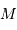 du centre de force à
partir des paramètres orbitaux
du centre de force à
partir des paramètres orbitaux 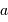 et
et 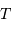 . Ces 2 termes sont en effet
observables, alors que la masse ne l'est pas.
. Ces 2 termes sont en effet
observables, alors que la masse ne l'est pas.
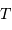 nécessite de repérer le mouvement le long de
la trajectoire.
nécessite de repérer le mouvement le long de
la trajectoire.
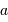
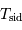

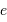
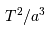
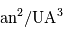
 sur l'
sur l'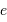 de l'orbite de chacune des 8 planètes, la relation
de l'orbite de chacune des 8 planètes, la relation 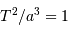 est vérifiée, avec
est vérifiée, avec 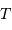 la période de révolution sidérale.
Les désaccords proviennent des écarts aux hypothèses de Kepler.
Remarque : dans le système solaire, les masses des planètes et de la
plupart de leurs satellites sont connues avec une précision relative de
l'ordre de
la période de révolution sidérale.
Les désaccords proviennent des écarts aux hypothèses de Kepler.
Remarque : dans le système solaire, les masses des planètes et de la
plupart de leurs satellites sont connues avec une précision relative de
l'ordre de 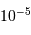 . Il s'agit de la précision à laquelle est mesurée
la constante gravitationnelle
. Il s'agit de la précision à laquelle est mesurée
la constante gravitationnelle 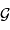 . Le produit
. Le produit 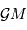 est souvent
déterminé avec une précision bien meilleure.
est souvent
déterminé avec une précision bien meilleure.

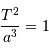
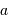 = 1 UA,
= 1 UA, 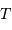 = 1 an, qui valide le cas de tout autre planète.
= 1 an, qui valide le cas de tout autre planète.
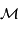 ,
la 3ème loi devient, toujours dans le système d'unités (UA, an,
,
la 3ème loi devient, toujours dans le système d'unités (UA, an,
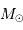 ) :
) :
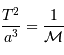
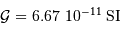
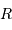 , de volume
, de volume 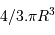
 .
.
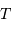 du mouvement du soleil autour du centre
galactique. L'exprimer en années.
du mouvement du soleil autour du centre
galactique. L'exprimer en années.
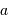 de la trajectoire du soleil autour du centre galactique, avec
de la trajectoire du soleil autour du centre galactique, avec
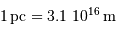 .
.
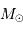 .
.
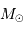 , avec
, avec
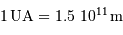 .
.
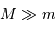 .
.
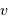 et du rayon de
courbure
et du rayon de
courbure 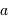 de la trajectoire.
de la trajectoire.
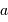 et à la période orbitale
et à la période orbitale 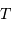 .
.
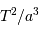 = 1 dans le système solaire
= 1 dans le système solaire
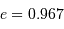 , Déterminer son
, Déterminer son 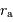 , son
, son
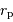 . Situer ces distances par rapport aux autres planètes.
. Situer ces distances par rapport aux autres planètes.
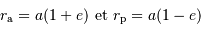
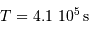 ,
, 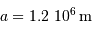 , et la constante gravitationnelle
, et la constante gravitationnelle 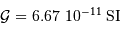 ,
,
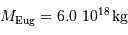
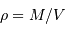 ,
,
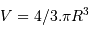 , on trouve :
, on trouve :
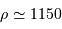 kg.m
kg.m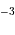 .
.
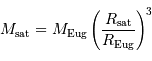
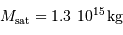 .
On peut vérifier, a posteriori et dans le cadre de l'hypothèse posée, que cette masse est très petite devant la masse du satellite principale, et que donc la 3ème loi de Kepler s'applique bien pour déterminer la masse d'Eugénie (cf. question 1).
.
On peut vérifier, a posteriori et dans le cadre de l'hypothèse posée, que cette masse est très petite devant la masse du satellite principale, et que donc la 3ème loi de Kepler s'applique bien pour déterminer la masse d'Eugénie (cf. question 1).
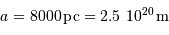 La détermination de la période résulte alors de la simple cinématique :
La détermination de la période résulte alors de la simple cinématique :
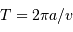 , soit
, soit 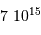 s : de
l'ordre de 230 millions d'années.
s : de
l'ordre de 230 millions d'années.
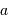 en UA donne :
en UA donne : 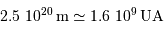 .
.
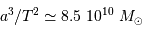 .
.