
 Peser un astéroide
Peser un astéroide
Difficulté : ☆
Temps : 15 min
Une équipe dirigée par W. Merline a observé en 1998 l'astéroïde
(45)Eugénie avec l'optique adaptative du télescope CFH. Les
observations
ont mis en évidence la présence d'un petit satellite.
Paramètres orbitaux
| Période | 4.7 j |
| Demi-grand axe | 1190 km |
| Diamètre de Eugénie | 215 km |
| Diamètre du satellite | 13 km |
Question 1)
Déterminer la masse de (45)Eugénie
AideSolution
Il s'agit d'une application de la 3ème loi de Kepler. On rappelle 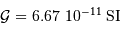
Le calcul en unités SI avec les données:
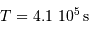 ,
, 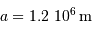 , et la constante gravitationnelle
, et la constante gravitationnelle 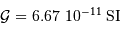 ,
,
aboutit par application de la 3e loi de Kepler à :
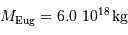
Question 2)
En déduire la masse volumique moyenne de Eugénie. Estimer sa
composition.
AideSolution
On suppose une forme sphérique de rayon 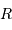 , de volume
, de volume 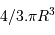
La masse volumique s'écrit : 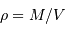 ,
,
avec le volume
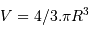 , on trouve :
, on trouve :
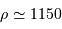 kg.m
kg.m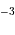 .
.
L'astéroïde (45)Eugénie semble peu dense, avec vraisemblablement un empilement lacunaire de roches.
Question 3)
Peut-on estimer la masse du petit satellite ?
AideSolution
Une hypothèse sur la masse volumique du petit satellite est nécessaire.
C'est impossible par la 3ème loi de Kepler. Une estimation, supposant
une masse volumique moyenne identique à celle de Eugénie, conduit à une
masse dans le rapport du cube des rayons :
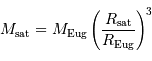
D'où : 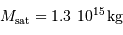 .
On peut vérifier, a posteriori et dans le cadre de l'hypothèse posée, que cette masse est très petite devant la masse du satellite principale, et que donc la 3ème loi de Kepler s'applique bien pour déterminer la masse d'Eugénie (cf. question 1).
.
On peut vérifier, a posteriori et dans le cadre de l'hypothèse posée, que cette masse est très petite devant la masse du satellite principale, et que donc la 3ème loi de Kepler s'applique bien pour déterminer la masse d'Eugénie (cf. question 1).

 Peser la Voie Lactée
Peser la Voie Lactée
Difficulté : ☆☆
Temps : 20 min
Notre galaxie, la Voie Lactée, a la forme d'une galette d'environ 30000 pc de diamètre et 2000 pc d'épaisseur. La région centrale est
formée d'un bulbe d'allure sphérique de 2 700 pc de rayon, qui
contient l'essentiel de la masse galactique.
Le Soleil orbite à 8000 pc du centre galactique.
D'après les mesures Doppler effectuées sur la raie à 21 cm de l'hydrogène,
l'orbite du Soleil est approximativement circulaire, et la vitesse
orbitale du Soleil est d'environ  .
.
Question 1)
Déterminer la période 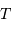 du mouvement du soleil autour du centre
galactique. L'exprimer en années.
du mouvement du soleil autour du centre
galactique. L'exprimer en années.
AideSolution
Commencer par déterminer le rayon 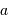 de la trajectoire du soleil autour du centre galactique, avec
de la trajectoire du soleil autour du centre galactique, avec
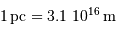 .
.
La conversion du rayon des pc aux m donne :
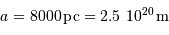 La détermination de la période résulte alors de la simple cinématique :
La détermination de la période résulte alors de la simple cinématique :
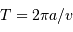 , soit
, soit 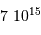 s : de
l'ordre de 230 millions d'années.
s : de
l'ordre de 230 millions d'années.
Question 2)
Estimer la masse du bulbe galactique,
en unité de masse solaire 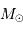 .
.
AideSolution
Mener le calcul en unités UA, an et 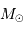 , avec
, avec
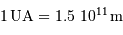 .
.
La mesure du rayon 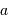 en UA donne :
en UA donne : 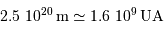 .
.
La 3e loi de Kepler aboutit alors à 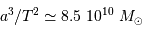 .
.
Le bulbe galactique
représente l'équivalent d'environ 85 milliards de soleils.

 .
.
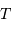 du mouvement du soleil autour du centre
galactique. L'exprimer en années.
du mouvement du soleil autour du centre
galactique. L'exprimer en années.