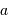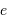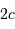Objectifs
Objectifs
Reconstituer les éléments géométriques de l'orbite vraie du système.
 Prérequis
Prérequis
Eléments géométriques définissant une trajectoire elliptique.
Demi-grand axe
L'observation donne une série de positions relatives des deux étoiles sur le ciel. En choisissant l'étoile la plus brillante (E2) comme origine des coordonnées, les positions de l'étoile la plus faible (E1) s'agencent sur une ellipse, mais il apparaît que E2 n'est pas au foyer de l'orbite projetée.
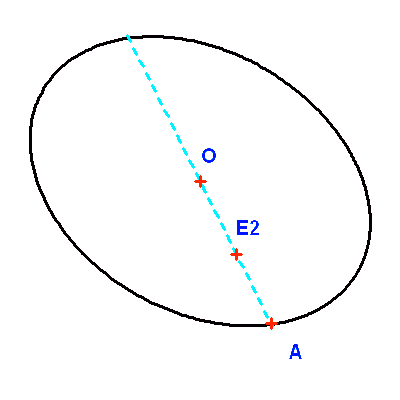
Ellipse et grand axe vus de biais.
Crédit :
ASM
Soit O le centre de l'ellipse apparente et A à l'intersection de la droite OE2 avec l'ellipse, au plus proche de E2 ; O est la projection du centre de l'orbite vraie et A est la projection de son périgée. Le segment [OA] est alors la projection du demi-grand axe de l'orbite vraie.
Excentricité
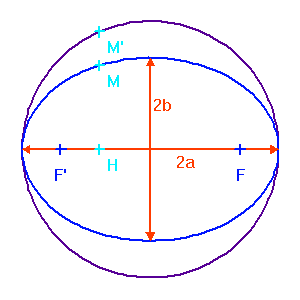
L'excentricité 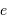 n'est pas plus conservée par la projection que le demi-grand axe, mais la détermination de l'excentricité de l'orbite réelle découle directement des paramètres de l'orbite projetée. Cette excentricité est en effet définie par la distance du foyer (E2) au centre (O), rapportée au demi-grand axe (0A). Ce rapport se mesure directement par OE2/OA, qui est conservé par la projection (par application du théorème de Thalès).
n'est pas plus conservée par la projection que le demi-grand axe, mais la détermination de l'excentricité de l'orbite réelle découle directement des paramètres de l'orbite projetée. Cette excentricité est en effet définie par la distance du foyer (E2) au centre (O), rapportée au demi-grand axe (0A). Ce rapport se mesure directement par OE2/OA, qui est conservé par la projection (par application du théorème de Thalès).
Cercle principal
Ellipse et son cercle principal.
Crédit :
ASM
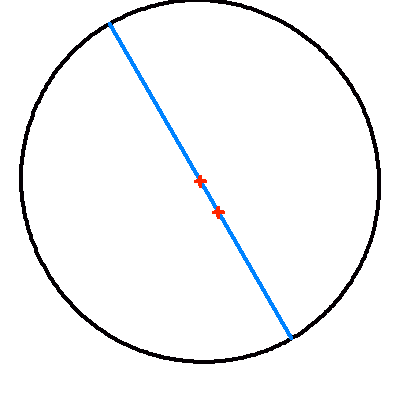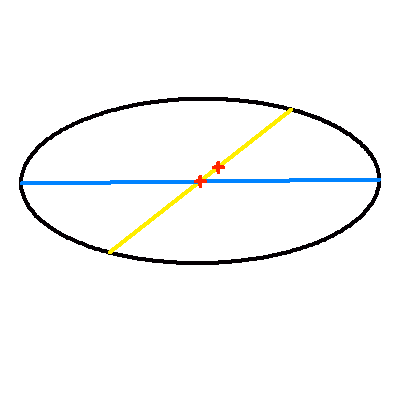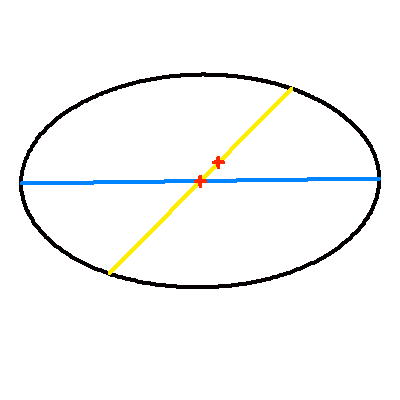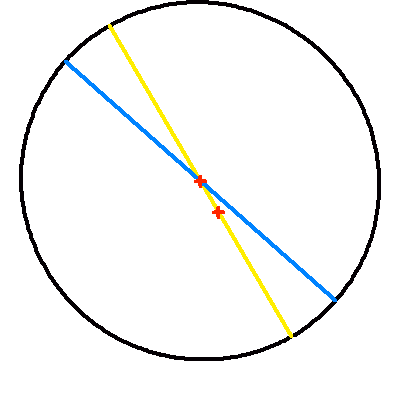
Projection dans le plan du ciel d'une orbite elliptique d'excentricité 0.2.
La droite jaune représente la projection du vrai demi-grand axe ; elle contient le centre et le foyer (occupé par la composante principale choisie comme origine). Le demi-grand axe apparent en en bleu.
Crédit :
ASM
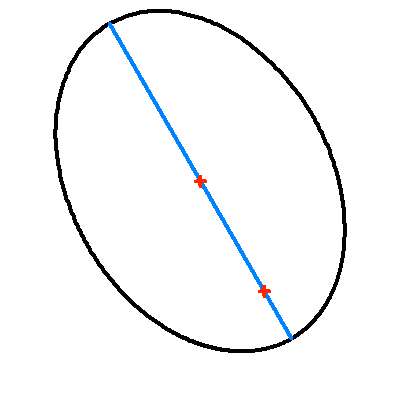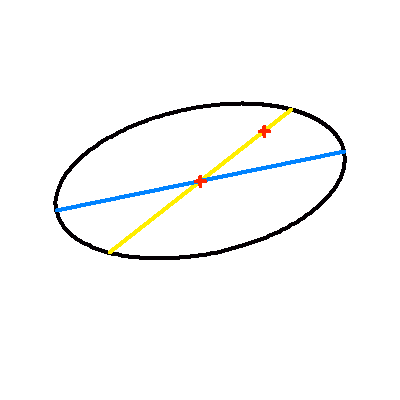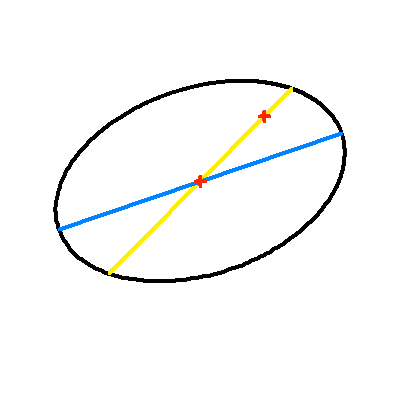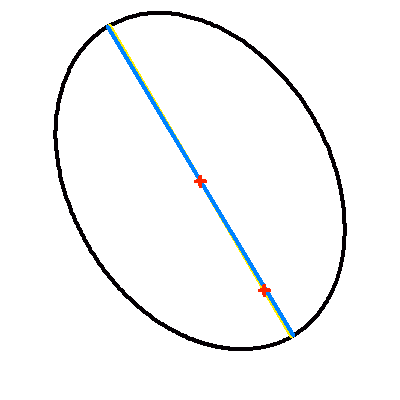
Projection dans le plan du ciel d'une orbite elliptique d'excentricité 0.7.
La droite jaune représente la projection du vrai demi-grand axe ; elle contient le centre et le foyer (occupé par la composante principale choisie comme origine). Le demi-grand axe apparent en en bleu.
Crédit :
ASM
Effet de projection
La projection du plan de l'orbite sur le plan du ciel modifie les paramètres de l'orbite apparente. Si le centre de l'ellipse est conservé par projection (la projection du centre de l'ellipse est égale au centre de l'ellipse projeté), le foyer ne l'est point : le demi-grand axe apparent se distingue (sauf dans certains cas très particuliers) de la projection du demi-grand axe.
L'animation met ce phénomène en évidence : elle montre l'apparence de la projection dans le plan du ciel d'une orbite elliptique, pour différentes inclinaisons. Étonnamment, l'effet est moins marqué dans le cas d'une excentricité plus grande.

L'orbite
L'appliquette donne la position de Sirius B par rapport à Sirius A.
- Tracer la trajectoire.
- Peut-on estimer directement les paramètres de la trajectoire ?
 Paramètres de l'orbite
Paramètres de l'orbite
Difficulté : ☆☆
Temps : 30 min
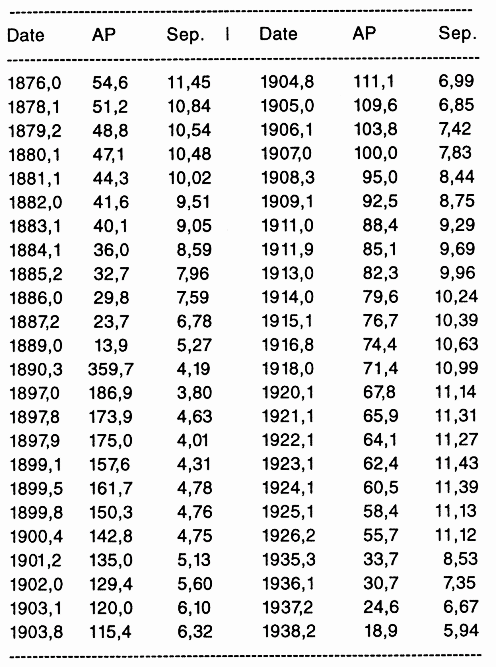
Angle de phase (en degré) et séparation (en "), en fonction de la date
Crédit :
ASM
En 1844, F.W. Bessel découvrit que Sirius présentait un mouvement propre, non linéaire, mais dont la modulation ressemblait à celle d'une étoile double visuelle. Il en conclut que le mouvement propre de Sirius était affecté par l'interaction gravitationnelle avec une seconde étoile de luminosité trop faible pour être observée. Ce compagnon fut observé pour la première fois en 1862 par A.G. Clark : cette étoile appelée Sirius B a une magnitude de 8.7 alors que celle de Sirius A vaut -1.4.

- L'appliquette ci-jointe donne les positions observées de Sirius B par rapport à Sirius A de 1876 à 1938, mesurées sur une suite de clichés photographiques. Chaque position est repérée par la séparation angulaire (en ") des deux étoiles et l'angle de position de la direction de Sirius B compté à partir de la direction Nord et dans le sens direct (0 deg pour la direction Nord et 90 deg pour la direction Est).
- Les positions successives ainsi reportées tracent l'orbite apparente de Sirius B par rapport à Sirius A, c'est-à-dire l'orbite telle qu'elle est observée sur le ciel.
- Les paramètres de l'ellipse représentant l'orbite apparente sont calculés par la méthode des moindres carrés. L'ellipse qui s'ajuste au mieux parmi les points observés est décrite par les paramètres du tableau.
| demi-grand axe | 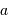 | 7.24" |
| excentricité | 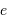 | 0.765 |
| distance entre les foyers | 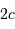 | 11.08" |
Question 1)
Sirius A, à l'intersection des axes, est-il au foyer de l'ellipse apparente ? Quelle conséquence en tire-t-on pour le plan de l'orbite ?
[1 points]
Question 2)
Déterminer la valeur de la période (en années).
[1 points]
Question 3)
Déterminer graphiquement le grand axe de l'ellipse vraie (il contient le centre de l'ellipse projetée (le centre est conservé par projection) et bien sûr Sirius A).
Déterminer les positions apparentes P et A du périastre et de l'apoastre et les dates qui leur correspondent.
[2 points]
Question 4)
Déterminer l'excentricité de l'orbite vraie.
[1 points]
 Objectifs
Objectifs Prérequis
Prérequis
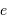 n'est pas plus conservée par la projection que le demi-grand axe, mais la détermination de l'excentricité de l'orbite réelle découle directement des paramètres de l'orbite projetée. Cette excentricité est en effet définie par la distance du foyer (E2) au centre (O), rapportée au demi-grand axe (0A). Ce rapport se mesure directement par OE2/OA, qui est conservé par la projection (par application du théorème de Thalès).
n'est pas plus conservée par la projection que le demi-grand axe, mais la détermination de l'excentricité de l'orbite réelle découle directement des paramètres de l'orbite projetée. Cette excentricité est en effet définie par la distance du foyer (E2) au centre (O), rapportée au demi-grand axe (0A). Ce rapport se mesure directement par OE2/OA, qui est conservé par la projection (par application du théorème de Thalès).

 de l'orbite vraie avec le plan du
ciel en reconstituant la projection du cercle principal de
l'ellipse vraie : ce cercle se projette suivant une ellipse dont
le rapport d'axes est égal à
de l'orbite vraie avec le plan du
ciel en reconstituant la projection du cercle principal de
l'ellipse vraie : ce cercle se projette suivant une ellipse dont
le rapport d'axes est égal à 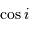 .
.
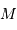 de l'ellipse coupe le cercle
principal en un point
de l'ellipse coupe le cercle
principal en un point 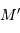 et le grand axe en un point
et le grand axe en un point 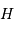 , tels
que
, tels
que 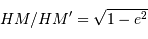 . Cette propriété se conservant par
projection on peut donc reconstituer l'ellipse projection du
cercle principal point par point à partir de la trajectoire
observée et de la direction conjuguée, i.e. la direction de la
tangente à l'ellipse observée aux points
. Cette propriété se conservant par
projection on peut donc reconstituer l'ellipse projection du
cercle principal point par point à partir de la trajectoire
observée et de la direction conjuguée, i.e. la direction de la
tangente à l'ellipse observée aux points 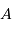 et
et 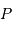 .
.
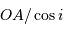 .
.