
Introduction |
Champ: Système Solaire
Temps: 2 à 3 heures, selon le niveau des élèves
Niveau: **
Savoir utiliser la règle de 3
Vous devrez être capable de déterminer la masse de Jupiter en mesurant les propriétés des orbites des satellites de Jupiter et en les analysant à l'aide de la troisième loi de Kepler.
Si vous apprenez à :
Vous pourrez :
On peut déduire certaines propriétés de corps célestes de leur mouvement même si on ne peut pas les mesurer directement. En 1543 Nicolaus Copernicus suppose que les planètes tournent sur des orbites circulaires autour du Soleil. Tycho Brahé observe soigneusement l'emplacement des planètes et de 777 étoiles pendant 20 ans en utilisant un sextant et un compas. Ces observations sont utilisées par Johannes Kepler, un étudiant de Tycho Brahé pour déduire de manière empirique trois lois mathématiques gouvernant l'orbite d'un objet par rapport à un autre. Pour une lune tournant autour d une planète, la troisième loi est
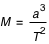 où
où
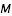 est la masse de la planète (comptée en masse solaire)
est la masse de la planète (comptée en masse solaire)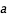 est le demi grand axe de l'orbite elliptique (compté en U.A., Unité Astronomique, qui est la distance moyenne du Soleil à la Terre)
est le demi grand axe de l'orbite elliptique (compté en U.A., Unité Astronomique, qui est la distance moyenne du Soleil à la Terre)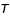 est la période (comptée en années terrestres). La période est le temps nécessaire au satellite pour faire un tour autour de la planète.
est la période (comptée en années terrestres). La période est le temps nécessaire au satellite pour faire un tour autour de la planète.En 1609, l'invention du télescope par Galilée permet l'observation d'objets invisibles à l'oeil nu. Galilée découvre que Jupiter est entouré de 4 satellites. Il les observe longuement. Le système de Jupiter était particulièrement important par sa ressemblance avec le système des planètes orbitant autour du Soleil. Son étude a aidé à comprendre les mouvements dans le système solaire. Le système de Jupiter montrait que le modèle héliocentrique du système solaire proposé par Copernic était physiquement possible. Malheureusement, l'inquisition s'inquiéta de ses découvertes et Galilée fut forcé de se renier. Ce sont les observations de Galilée et les calculs de Kepler que vous allez refaire ici.