Dimensions et unités physiques

Auteur: Stéphane Erard

Les formules mathématiques utilisées en Astronomie définissent des relations entre grandeurs physiques. Ces grandeurs ont une dimension physique, et sont mesurées dans une certaine unité.

La dimension est inhérente à une grandeur physique, sa valeur est fonction de l'unité utilisée. On distingue sept types de grandeurs physiques, ou dimensions, indépendantes. Toute quantité physique peut s'exprimer comme combinaison de ces grandeurs de base.

Le système officiel en vigueur est le SI (Système International d'unités) ou MKSA, qui définit les unités de mesure des sept grandeurs indépendantes (voir par exemple la définition de la seconde). Différents systèmes d'unités ont été utilisés au cours de l'histoire, et d'autres systèmes sont en usage dans des domaines particuliers. En Astronomie, on utilise couramment des unités en rapport avec les phénomènes étudiés, par exemple l'unité astronomique, l'année-lumière, le parsec, ou le décalage vers le rouge pour les distances.

Table 1
Grandeur de base	Dimension	Unité S. I.	Symbole S. I.
Longueur	L	mètre	m
Masse	M	kilogramme	kg
Temps	T	seconde	s
Intensité de courant	I	Ampère	A
Température	Θ	Kelvin	K
Quantité de matière	N	mole	mol
Intensité lumineuse	J	candela	cd

Deux autres grandeurs sont utilisées en complément de celles-ci. Elles sont dépourvues de dimension physique (elles peuvent être comprises comme des rapports de longueurs ou de surfaces), mais peuvent s'exprimer dans différentes échelles. En pratique, on préfère l'échelle qui n'introduit pas de coefficient dans les fonctions trigonométriques (en radians, par opposition aux degrés pour les angles plats).

Table 2
Grandeur dérivée	Dimension	Unité S. I.	Symbole S. I.
Angle plan	1	radian	rad
Angle solide	1	stéradian	sr

Ecrire une équation aux dimensions consiste à remplacer dans une formule les grandeurs par leurs dimensions et à négliger les coefficients de proportionnalité.

Exemple

La définition de la vitesse donne la dimension physique de cette grandeur :

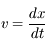
$v= \frac{dx}{dt}$

L'équation aux dimensions est :

$[V] = LT^{-1}$

et la vitesse se mesure en m/s dans le Système International.