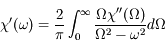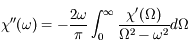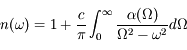On trouvera dans cette partie les exercices suivants :
- Excentricité limite dans les développements du problème des deux corps
- Dérivation des relations de Kramers-Kronig par le théorème des résidus
Auteur: Alain Vienne
En mécanique céleste, il est quelque fois utile d'utiliser certaines formules du problème à 2 corps (ou problème keplerien) sous forme de développements. Cela permet, en théorie des perturbations, de faire des calculs analytiques.
Par exemple, l'"équation du centre", qui donne la position du corps sur son orbite en fonction du temps, est:
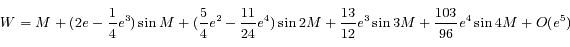
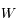 est l'anomalie vraie, c'est à dire l'angle qui positionne le corps sur son orbite à partir de la direction du minimum de distance (péricentre ).
est l'anomalie vraie, c'est à dire l'angle qui positionne le corps sur son orbite à partir de la direction du minimum de distance (péricentre ). 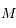 est le temps ou plus précisément c'est l'anomalie moyenne
est le temps ou plus précisément c'est l'anomalie moyenne 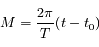 avec
avec 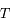 la période,
la période, 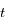 le temps et
le temps et 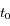 l'instant de passage au péricentre.
l'instant de passage au péricentre.  est l'excentricité.
est l'excentricité.
Attention cette formule est bien une série entière en  (mais tronquée à l'ordre 4). Cela aurait été plus net si on l'avait écrit comme:
(mais tronquée à l'ordre 4). Cela aurait été plus net si on l'avait écrit comme:
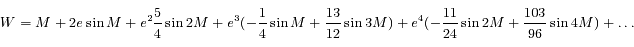
Mais, en fait, on préfère l'écriture en série de Fourier, c'est-à-dire:
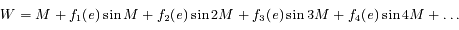
En tant que série de Fourier, la convergence ne pose pas de problème car la fonction à considérer est de classe 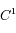 par rapport à la variable
par rapport à la variable 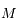 . Seulement, dès que les
. Seulement, dès que les 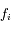 sont tronqués à un certain ordre en excentricité, cela revient à considérer la série entière.
sont tronqués à un certain ordre en excentricité, cela revient à considérer la série entière.
L'exercice qui est proposé utilise le théorème de Lagrange pour montrer que la série entière ci-dessus (et toutes celles du problème des 2-corps) converge si 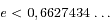 . Cela signifie que ces séries ne peuvent être utilisées que pour des excentricités bien en deça de cette valeur. Evidemment, la solution du problème à 2 corps elle-même existe quelque soit l'excentricité.
. Cela signifie que ces séries ne peuvent être utilisées que pour des excentricités bien en deça de cette valeur. Evidemment, la solution du problème à 2 corps elle-même existe quelque soit l'excentricité.
Un autre exercice avec ce théorème est disponible ici.
Auteur: Alain Vienne
 Excentricité limite dans les développements du problème à 2 corps
Excentricité limite dans les développements du problème à 2 corps
Difficulté : ☆☆☆
Temps : 1h30
 Introduction
Introduction
Dans le problème à 2 corps (voir, pour plus de détails, un cours d'astronomie, par exemple celui-ci) l'anomalie vraie et l'anomalie moyenne sont liées grâce à l'anomalie excentrique 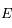 par les 2 formules suivantes:
par les 2 formules suivantes:
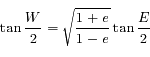 , et
, et
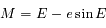 qui est appelée "équation de Képler".
qui est appelée "équation de Képler".
Question 1)
Sachant que  est le petit paramètre, montrer que l'équation de Kepler est de la forme indiquée dans le théorème de Lagrange. Indiquer à quoi correspond chacun des paramètres de ce théorème dans notre problème.
est le petit paramètre, montrer que l'équation de Kepler est de la forme indiquée dans le théorème de Lagrange. Indiquer à quoi correspond chacun des paramètres de ce théorème dans notre problème.
Il suffit d'identifier en acceptant que 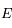 soit complexe. De plus
soit complexe. De plus 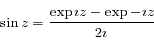 qui est une fonction complexe.
qui est une fonction complexe.
Question 4)
Que devient 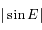 pour ces conditions?
pour ces conditions?
Auteur: Stéphane Erard
Les relations de Kramers-Kronig relient les indices de réfraction réel et imaginaire d'un même milieu matériel. Ceux-ci, bien qu'on les appelle couramment constantes optiques, varient en fonction de la longueur d'onde d'une façon caractéristique de la composition du milieu. A ce titre, ils jouent un rôle particulièrement important en Astrophysique puisque l'étude de la lumière produite, absorbée ou réfléchie par un astre distant permet de connaître sa composition.
La partie réelle de l'indice (généralement appelée indice de réfraction) intervient dans les lois de Snell-Descartes, la partie imaginaire (coefficient d'absorption) rendant compte de l'absorption au cours de la propagation dans le milieu. La mesure simultanée des deux quantités est difficile ; les relations de Kramers-Kronig qui permettent de calculer l'un en connaissant l'autre ont donc une grande importance pratique en spectroscopie de laboratoire.
Auteur: Stéphane Erard
 Relations de Kramers-Kronig
Relations de Kramers-Kronig
Difficulté : ☆☆
Temps : 60 min
Les équations de Maxwell dans un milieu matériel font intervenir un vecteur induction électrique défini comme :
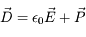
où 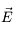 est le champ électrique appliqué,
est le champ électrique appliqué, 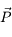 la polarisation électrique du milieu (qui décrit la réaction du milieu à l'application du champ électrique externe) et
la polarisation électrique du milieu (qui décrit la réaction du milieu à l'application du champ électrique externe) et 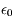 une constante physique appelée permittivité du vide.
une constante physique appelée permittivité du vide.
Les propriétés du milieu lui-même sont décrites par un certain type de relation entre le champ électrique et la polarisation. Dans un grand nombre de cas (milieu isotrope, champ faible...) cette relation peut s'écrire :
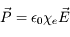
où 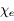 (la susceptibilité électrique) est a priori un tenseur d'ordre 2 dépendant du temps et de la position.
(la susceptibilité électrique) est a priori un tenseur d'ordre 2 dépendant du temps et de la position.
La solution des équations de Maxwell dans le milieu met en évidence l'indice de réfraction complexe de ce milieu :
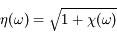
où 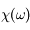 est la représentation en fréquence de
est la représentation en fréquence de 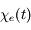 , c'est-à-dire sa transformée de Fourier.
, c'est-à-dire sa transformée de Fourier.
Question 1)
On considère un milieu linéaire, tel que :
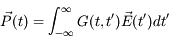
Que représente la fonction G ?
Remplacer le champ électrique par une impulsion 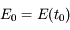
Question 2)
Déduire en utilisant le théorème de convolution une relation entre les représentations en fréquence du champ électrique et de la polarisation, puis entre G et 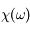 .
.
Question 3)
En supposant constantes les propriétés du milieu, comment peut-on simplifier la fonction G ?
Puisque les propriétés du milieu sont constantes au cours du temps, G ne doit pas dépendre du moment considéré (t) mais seulement de l'intervalle de temps écoulé depuis l'application du champ électrique, (t-t').
Par ailleurs, la fonction G doit être causale : la polarisation du milieu ne peut dépendre que du champ appliqué avant l'instant t considéré.
Question 4)
On considère la fonction 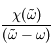 de la variable complexe
de la variable complexe 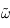 , où
, où 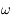 est réel. Montrer qu'elle est analytique dans la partie supérieure du plan complexe.
est réel. Montrer qu'elle est analytique dans la partie supérieure du plan complexe.
Question 5)
Trouver un contour d'intégration adéquat pour calculer l'intégrale de 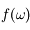 . Calculer l'intégrale. Commentaire ?
. Calculer l'intégrale. Commentaire ?
Question 6)
En déduire une relation entre parties réelle et imaginaire de 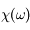 .
.
Question 7)
En explicitant les symétries de 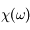 , trouver une autre écriture de ces relations.
, trouver une autre écriture de ces relations.
Question 8)
On écrit l'indice de réfraction en fonction de l'indice réel n et du coefficient d'absorption 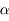 , avec c = vitesse de la lumière :
, avec c = vitesse de la lumière :
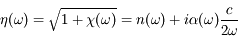
Ecrire n en fonction de 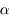 (ce sont les deux quantités directement mesurables). Quel est l'intérêt pratique de cette relation ?
(ce sont les deux quantités directement mesurables). Quel est l'intérêt pratique de cette relation ?
On suppose le milieu suffisamment dilué pour que
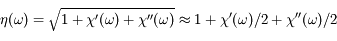
-
Question 1
Aide :
Remplacer le champ électrique par une impulsion 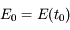
Solution :
La polarisation est alors 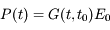
G est donc la réponse impulsionnelle (polarisation résultant d'une impulsion unité, en l'occurrence un champ électrique externe appliqué pendant un court instant).
-
Question 2
Solution :
Le théorème de convolution donne directement :
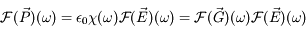
où 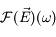 dénote la transformée de Fourier du champ électrique (fonction de la fréquence
dénote la transformée de Fourier du champ électrique (fonction de la fréquence 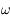 ) et où
) et où 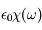 est celle de G(t). On a donc :
est celle de G(t). On a donc :
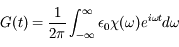 et
et
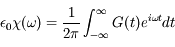
-
Question 3
Aide :
Puisque les propriétés du milieu sont constantes au cours du temps, G ne doit pas dépendre du moment considéré (t) mais seulement de l'intervalle de temps écoulé depuis l'application du champ électrique, (t-t').
Aide :
Par ailleurs, la fonction G doit être causale : la polarisation du milieu ne peut dépendre que du champ appliqué avant l'instant t considéré.
Solution :
On peut donc écrire G(t,t') = G(t-t'), avec G(t) = 0 pour t < 0. On a donc :
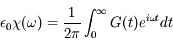
-
Question 4
Aide :
Si 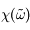 est analytique, la fonction
est analytique, la fonction 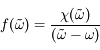 l'est aussi sauf au pôle
l'est aussi sauf au pôle 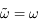 , situé sur l'axe réel.
, situé sur l'axe réel.
Solution :
Pour 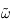 réel,
réel, 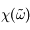 est défini comme la transformée de Fourier de G, elle est donc analytique.
est défini comme la transformée de Fourier de G, elle est donc analytique.
Pour tout t ≥ 0, 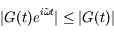 dans la partie supérieure du plan complexe (où
dans la partie supérieure du plan complexe (où 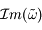 >0).
>0).
La définition assure que 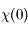 est fini, ce qui implique que
est fini, ce qui implique que 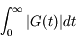 converge.
converge.
Ces deux dernières conditions assurent que 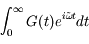 converge dans la partie supérieure du plan complexe.
converge dans la partie supérieure du plan complexe.
-
Question 5
Solution :
On utilise le contour suivant, en faisant tendre 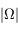 vers l'infini sur
vers l'infini sur 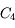 , et vers 0 sur
, et vers 0 sur 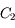 .
Le théorème de Cauchy assure que l'intégrale le long de ce contour est nulle :
.
Le théorème de Cauchy assure que l'intégrale le long de ce contour est nulle :
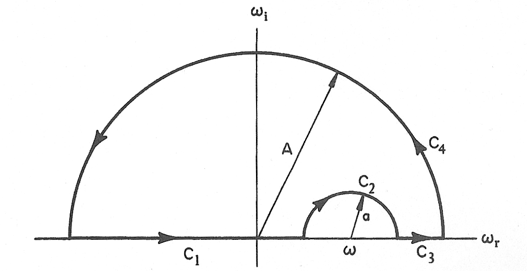
Contour d'intégration pour le calcul de l'intégrale
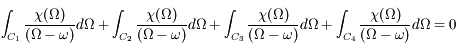
En appelant 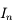 l'intégrale sur le contour
l'intégrale sur le contour 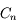 ,
, 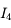 tend vers 0, la somme
tend vers 0, la somme 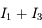 tend vers l'intégrale cherchée, et
tend vers l'intégrale cherchée, et 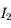 est donnée par le théorème de résidus. On a au total :
est donnée par le théorème de résidus. On a au total :
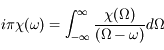
soit une relation entre 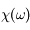 et son intégrale avec un coefficient imaginaire, ce qui implique une relation entre les parties réelle et imaginaire de
et son intégrale avec un coefficient imaginaire, ce qui implique une relation entre les parties réelle et imaginaire de 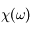 .
.
-
Question 6
Solution :
En posant 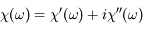 on a :
on a :
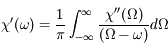
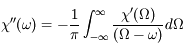
-
Question 7
Solution :
La fonction 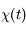 étant réelle, le complexe conjugué de sa représentation en fréquence est tel que
étant réelle, le complexe conjugué de sa représentation en fréquence est tel que 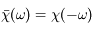 . En d'autres termes,
. En d'autres termes, 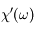 est paire et
est paire et 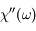 est impaire. En remplaçant dans l'expression précédente, on trouve :
est impaire. En remplaçant dans l'expression précédente, on trouve :
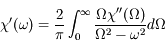
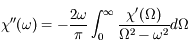
-
Question 8
Aide :
On suppose le milieu suffisamment dilué pour que
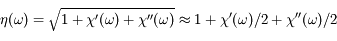
Solution :
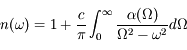
Le coefficient d'absorption se mesure facilement en transmission. Sa connaissance sur un domaine spectral suffisamment étendu permet de calculer l'indice réel à toute fréquence.
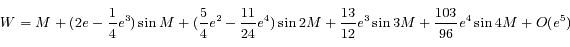
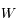 est l'anomalie vraie, c'est à dire l'angle qui positionne le corps sur son orbite à partir de la direction du minimum de distance (péricentre ).
est l'anomalie vraie, c'est à dire l'angle qui positionne le corps sur son orbite à partir de la direction du minimum de distance (péricentre ). 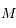 est le temps ou plus précisément c'est l'anomalie moyenne
est le temps ou plus précisément c'est l'anomalie moyenne 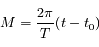 avec
avec 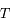 la période,
la période, 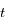 le temps et
le temps et 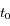 l'instant de passage au péricentre.
l'instant de passage au péricentre.  est l'excentricité.
est l'excentricité.
 (mais tronquée à l'ordre 4). Cela aurait été plus net si on l'avait écrit comme:
(mais tronquée à l'ordre 4). Cela aurait été plus net si on l'avait écrit comme:
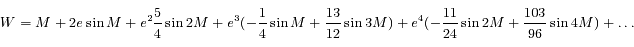
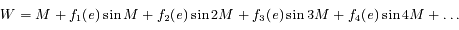
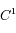 par rapport à la variable
par rapport à la variable 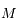 . Seulement, dès que les
. Seulement, dès que les 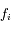 sont tronqués à un certain ordre en excentricité, cela revient à considérer la série entière.
sont tronqués à un certain ordre en excentricité, cela revient à considérer la série entière.
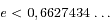 . Cela signifie que ces séries ne peuvent être utilisées que pour des excentricités bien en deça de cette valeur. Evidemment, la solution du problème à 2 corps elle-même existe quelque soit l'excentricité.
. Cela signifie que ces séries ne peuvent être utilisées que pour des excentricités bien en deça de cette valeur. Evidemment, la solution du problème à 2 corps elle-même existe quelque soit l'excentricité.
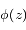 de la variable complexe
de la variable complexe 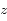 . Soient
. Soient 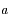 et
et 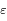 des complexes.
des complexes.
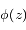 est analytique à l'intérieur du contour
est analytique à l'intérieur du contour 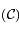 du plan complexe entourant le point
du plan complexe entourant le point 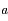 avec
avec 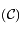 tel que :
tel que : 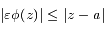
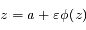 a une raçine développable dans l'intérieur de
a une raçine développable dans l'intérieur de 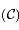 en série entière de
en série entière de 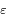 :
:
![z= a + \sum_{n=1}^{\infty} \frac{\varepsilon ^n}{n!}\bigg[\frac{d^{n-1}}{dz^{n-1}}[\phi (z)]^n\bigg]_{z=a}](../pages_residus/equations_residus/equation28.png)
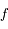 analytique dans
analytique dans 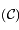 ,
, 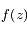 peut aussi être développée:
peut aussi être développée:
![f(z)= f(a) + \sum_{n=1}^{\infty} \frac{\varepsilon ^n}{n!}\bigg[\frac{d^{n-1}}{dz^{n-1}}\bigg( \frac{df}{dz}[\phi (z)]^n \bigg) \bigg]_{z=a}](../pages_residus/equations_residus/equation32.png)
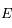 par les 2 formules suivantes:
par les 2 formules suivantes:
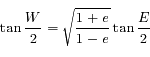 , et
, et
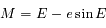 qui est appelée "équation de Képler".
qui est appelée "équation de Képler".
 est le petit paramètre, montrer que l'équation de Kepler est de la forme indiquée dans le théorème de Lagrange. Indiquer à quoi correspond chacun des paramètres de ce théorème dans notre problème.
est le petit paramètre, montrer que l'équation de Kepler est de la forme indiquée dans le théorème de Lagrange. Indiquer à quoi correspond chacun des paramètres de ce théorème dans notre problème.
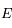 soit complexe. De plus
soit complexe. De plus 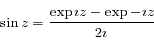 qui est une fonction complexe.
qui est une fonction complexe.
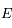 est donc complexe. On suppose
est donc complexe. On suppose 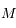 réel et on pose:
réel et on pose: 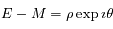 (module et argument). Exprimer
(module et argument). Exprimer 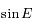 puis
puis 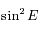 en fonction de
en fonction de 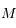 ,
, 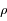 et
et 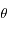
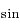 , puis les fonctions réelles trigonométriques circulaires et hyperboliques avec les variables
, puis les fonctions réelles trigonométriques circulaires et hyperboliques avec les variables 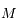 ,
, 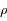 et
et 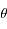 .
.
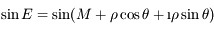 puis utiliser la formule d'addition. Puis que
puis utiliser la formule d'addition. Puis que 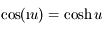 (de même avec le sinus)
(de même avec le sinus)
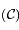 est défini par
est défini par 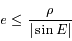 . Le cas le plus défavorable correspond à
. Le cas le plus défavorable correspond à 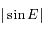 maximum. Donner les conditions sur
maximum. Donner les conditions sur 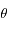 et
et 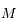 correspondantes.
correspondantes.
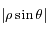 maximum et
maximum et
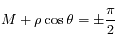
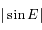 pour ces conditions?
pour ces conditions?
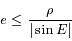 , on cherche donc à maximiser
, on cherche donc à maximiser 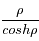 . Montrer que ce maximum est atteint pour
. Montrer que ce maximum est atteint pour 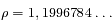 En déduire la plus grande valeur de l'exentricité
En déduire la plus grande valeur de l'exentricité 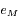 .
.
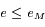 , on peut écrire:
, on peut écrire: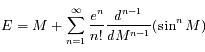 . Pour obtenir l'équation du centre, il faut encore utiliser la formule
. Pour obtenir l'équation du centre, il faut encore utiliser la formule 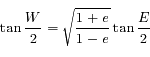 pour revenir à
pour revenir à 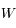 . Mais cette formule ne pose aucun problème de convergence. La valeur de
. Mais cette formule ne pose aucun problème de convergence. La valeur de 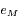 est donc inchangée.
est donc inchangée.
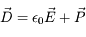
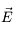 est le champ électrique appliqué,
est le champ électrique appliqué, 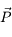 la polarisation électrique du milieu (qui décrit la réaction du milieu à l'application du champ électrique externe) et
la polarisation électrique du milieu (qui décrit la réaction du milieu à l'application du champ électrique externe) et 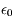 une constante physique appelée permittivité du vide.
une constante physique appelée permittivité du vide.
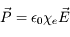
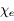 (la susceptibilité électrique) est a priori un tenseur d'ordre 2 dépendant du temps et de la position.
(la susceptibilité électrique) est a priori un tenseur d'ordre 2 dépendant du temps et de la position.
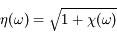
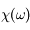 est la représentation en fréquence de
est la représentation en fréquence de 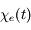 , c'est-à-dire sa transformée de Fourier.
, c'est-à-dire sa transformée de Fourier.
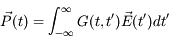
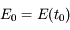
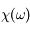 .
.
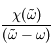 de la variable complexe
de la variable complexe 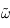 , où
, où 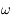 est réel. Montrer qu'elle est analytique dans la partie supérieure du plan complexe.
est réel. Montrer qu'elle est analytique dans la partie supérieure du plan complexe.
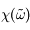 est analytique, la fonction
est analytique, la fonction 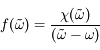 l'est aussi sauf au pôle
l'est aussi sauf au pôle 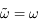 , situé sur l'axe réel.
, situé sur l'axe réel.
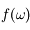 . Calculer l'intégrale. Commentaire ?
. Calculer l'intégrale. Commentaire ?
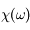 .
.
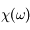 , trouver une autre écriture de ces relations.
, trouver une autre écriture de ces relations.
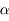 , avec c = vitesse de la lumière :
, avec c = vitesse de la lumière :
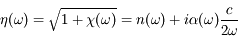
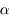 (ce sont les deux quantités directement mesurables). Quel est l'intérêt pratique de cette relation ?
(ce sont les deux quantités directement mesurables). Quel est l'intérêt pratique de cette relation ?
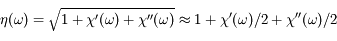
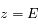 ,
, 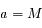 ,
, 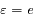 et
et 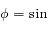
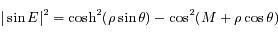
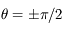 et
et 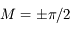
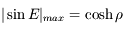
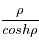 est maximum pour
est maximum pour 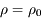 racine de l'équation
racine de l'équation 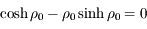 . Une résolution numérique (dichotomie, newton, ....) donne
. Une résolution numérique (dichotomie, newton, ....) donne 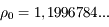 . Donc
. Donc 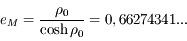
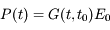
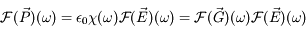
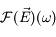 dénote la transformée de Fourier du champ électrique (fonction de la fréquence
dénote la transformée de Fourier du champ électrique (fonction de la fréquence 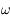 ) et où
) et où 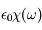 est celle de G(t). On a donc :
est celle de G(t). On a donc :
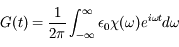 et
et
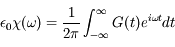
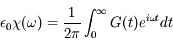
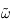 réel,
réel, 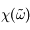 est défini comme la transformée de Fourier de G, elle est donc analytique.
est défini comme la transformée de Fourier de G, elle est donc analytique.
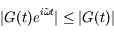 dans la partie supérieure du plan complexe (où
dans la partie supérieure du plan complexe (où 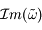 >0).
>0).
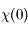 est fini, ce qui implique que
est fini, ce qui implique que 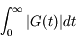 converge.
converge.
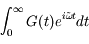 converge dans la partie supérieure du plan complexe.
converge dans la partie supérieure du plan complexe.
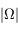 vers l'infini sur
vers l'infini sur 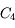 , et vers 0 sur
, et vers 0 sur 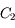 .
Le théorème de Cauchy assure que l'intégrale le long de ce contour est nulle :
.
Le théorème de Cauchy assure que l'intégrale le long de ce contour est nulle :

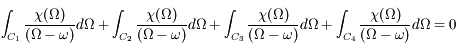
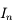 l'intégrale sur le contour
l'intégrale sur le contour 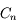 ,
, 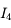 tend vers 0, la somme
tend vers 0, la somme 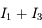 tend vers l'intégrale cherchée, et
tend vers l'intégrale cherchée, et 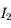 est donnée par le théorème de résidus. On a au total :
est donnée par le théorème de résidus. On a au total :
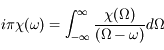
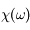 et son intégrale avec un coefficient imaginaire, ce qui implique une relation entre les parties réelle et imaginaire de
et son intégrale avec un coefficient imaginaire, ce qui implique une relation entre les parties réelle et imaginaire de 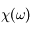 .
.
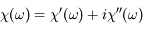 on a :
on a :
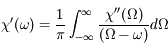
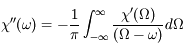
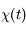 étant réelle, le complexe conjugué de sa représentation en fréquence est tel que
étant réelle, le complexe conjugué de sa représentation en fréquence est tel que 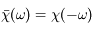 . En d'autres termes,
. En d'autres termes, 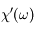 est paire et
est paire et 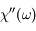 est impaire. En remplaçant dans l'expression précédente, on trouve :
est impaire. En remplaçant dans l'expression précédente, on trouve :