Théorème d'inversion de Lagrange

Auteurs: Jérôme Thiébaut, Marc Fouchard, S. Renner

Auteur: S. Renner

Le théorème d'inversion de Lagrange donne le développement en série d'une fonction définie implicitement. L'application de ce théorème permet entre autres d'obtenir une solution numérique de l'équation de Kepler 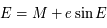$E = M + e \sin E$ , ou d'écrire des développements utiles du problème des deux corps.

Voici un énoncé de ce théorème :

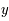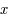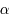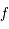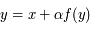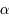Soit fonction de 2 variables et $\alpha$ et d'une fonction infiniment dérivable de la forme : $y = x + \alpha f(y)$ avec $\alpha$ petit.

Alors 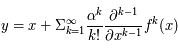$\displyastyle y = x + \Sigma_{k=1}^\infty \frac{\alpha^k}{k!} \frac{\partial^{k-1}}{\partial x^{k-1}} f^k(x)$ .

On propose ici de le démontrer par une méthode reposant sur les dérivées partielles, révélée par Pierre-Simon Laplace.