Auteur: Marc Fouchard
 Paramètre de Tisserand
Paramètre de Tisserand
Difficulté : ☆
Temps : 1h30
On considère un problème de trois corps où les deux premiers 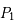 et
et 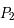 , appelés primaires et de masse respective
, appelés primaires et de masse respective 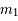 et
et 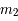 , sont sur des orbites circulaires et uniforme ; et le troisième
, sont sur des orbites circulaires et uniforme ; et le troisième 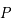 , de masse
négligeable voit sa trajectoire affectée
par les primaires alors que celui-ci n'affecte pas le mouvement des deux primaires. Ce problème est appelé le problème de trois corps restreint et circulaire.
, de masse
négligeable voit sa trajectoire affectée
par les primaires alors que celui-ci n'affecte pas le mouvement des deux primaires. Ce problème est appelé le problème de trois corps restreint et circulaire.
On considère un repère tournant orthonormé, centré sur le centre de gravité 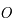 des deux primaires et dont les axes sont tels que l'axe des abscisses est dirigé vers le deuxième primaire, l'axe des ordonnées fait un angle de
des deux primaires et dont les axes sont tels que l'axe des abscisses est dirigé vers le deuxième primaire, l'axe des ordonnées fait un angle de 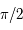 avec celui des abscisse dans le même sens que le mouvement de rotation des primaires, et l'axe des
avec celui des abscisse dans le même sens que le mouvement de rotation des primaires, et l'axe des 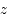 complète un trièdre direct.
complète un trièdre direct.
On considère aussi un repère fixe orthonormé qui coïncide avec le repère tournant à 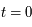 .
.
Dans le repère tournant, les coordonnées des deux primaires sont 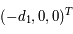 et
et 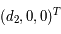 , où
, où 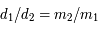 et
et 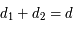 qui est la distance (fixe) qui sépare les deux primaires. On note
qui est la distance (fixe) qui sépare les deux primaires. On note 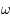 la vitesse de rotation angulaire des deux primaires par rapport au repère fixe.
la vitesse de rotation angulaire des deux primaires par rapport au repère fixe.
De manière générale on notera 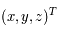 les coordonnées dans le repère fixe et
les coordonnées dans le repère fixe et 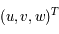 les coordonnées dans le repère tournant.
Le point au dessus d'une quantité indique la dérivée par rapport au temps de cette quantité.
les coordonnées dans le repère tournant.
Le point au dessus d'une quantité indique la dérivée par rapport au temps de cette quantité.
Question 2)
Déterminer les formules de passage entre 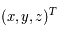 et
et 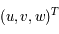 pour un même objet.
pour un même objet.
Question 4)
En différenciant les expressions de 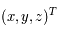 en fonction de
en fonction de 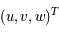 , en déduire les équations du mouvement dans le repère tournant.
, en déduire les équations du mouvement dans le repère tournant.
Question 5)
Montrer qu'il existe une fonction 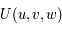 tel que le système d'équations précédent s'écrit :
tel que le système d'équations précédent s'écrit :
 ,
,
Question 6)
En multipliant chaque ligne du système précédent par  ,
,  et
et 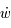 respectivement, puis en additionnant, montrer que le système admet une intégrale du mouvement (c'est -à-dire une quantité qui est constante au cours du temps).
respectivement, puis en additionnant, montrer que le système admet une intégrale du mouvement (c'est -à-dire une quantité qui est constante au cours du temps).
Question 7)
En déduire 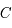 en fonction de
en fonction de 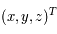 et de leur dérivées par rapport au temps.
et de leur dérivées par rapport au temps.
 Entropie
Entropie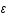 , aux variations d'entropie, S, et de volume, V, par la relation suivante:
, aux variations d'entropie, S, et de volume, V, par la relation suivante:
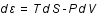 ,
où T est la température et P la pression.
,
où T est la température et P la pression.
 .
.
 .
.
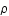 puis relier l'entropie à ces variables thermodynamiques.
puis relier l'entropie à ces variables thermodynamiques.
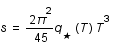 , où
, où 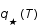 est un facteur dépendant de la température et des particules présentes. L'unité de volume est
est un facteur dépendant de la température et des particules présentes. L'unité de volume est 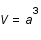 , où
, où 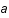 est le facteur d'échelle mesurant l'expansion de l'univers. Exprimer S comme une fonction de la température T et du facteur d'échelle a.
est le facteur d'échelle mesurant l'expansion de l'univers. Exprimer S comme une fonction de la température T et du facteur d'échelle a.
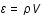
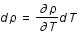
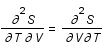 .
.
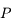 de masse unité mobile dans un plan et soumis à l'attraction gravitationnelle d'un corps fixe de masse
de masse unité mobile dans un plan et soumis à l'attraction gravitationnelle d'un corps fixe de masse 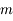 se trouvant en
se trouvant en 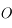 . On suppose que
. On suppose que 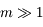 .
.
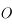 . On précise que la force universelle de la gravitation
s'appliquant au point
. On précise que la force universelle de la gravitation
s'appliquant au point 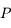 est:
est:
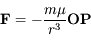 ,
,
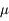 désigne la constante universelle de la gravitation et
désigne la constante universelle de la gravitation et 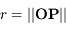 (les notations en gras dénotent des vecteurs).
(les notations en gras dénotent des vecteurs).
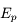 .
.
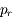 et
et 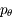 associées aux coordonnées
associées aux coordonnées 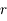 et
et 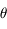 .
.
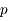 associée à la coordonnée
associée à la coordonnée 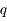 est définie par :
est définie par : 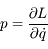 .
.
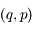 on a les équations:
on a les équations:
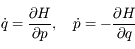 .
.
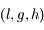 associées aux moments conjuguées
associées aux moments conjuguées 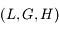 (voir ce
(voir ce 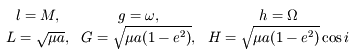 .
.
 est
est  est
est  est
est 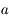 est
est 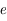 est
est  est
est 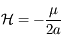 , (voir cet exercice sur l'
, (voir cet exercice sur l'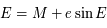 , ou d'écrire des développements utiles du problème des deux corps.
, ou d'écrire des développements utiles du problème des deux corps.
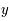 fonction de 2 variables
fonction de 2 variables 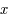 et
et 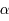 et d'une fonction
et d'une fonction 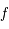 infiniment dérivable de la forme :
infiniment dérivable de la forme : 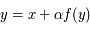 avec
avec 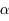 petit.
petit.
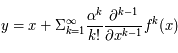 .
.
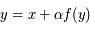 , alors
, alors 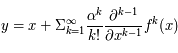 avec
avec 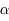 petit.
petit.
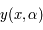 au voisinage de
au voisinage de 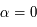 .
.
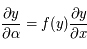 .
.
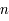 strictement positif,
strictement positif, 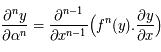 . On utilisera le résultat de la question précédente.
. On utilisera le résultat de la question précédente.
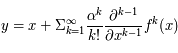 .
.
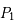 et
et 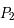 , appelés primaires et de masse respective
, appelés primaires et de masse respective 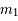 et
et 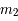 , sont sur des orbites circulaires et
, sont sur des orbites circulaires et 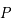 , de masse
négligeable voit sa trajectoire affectée
par les primaires alors que celui-ci n'affecte pas le mouvement des deux primaires. Ce problème est appelé le problème de trois corps restreint et circulaire.
, de masse
négligeable voit sa trajectoire affectée
par les primaires alors que celui-ci n'affecte pas le mouvement des deux primaires. Ce problème est appelé le problème de trois corps restreint et circulaire.
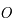 des deux primaires et dont les axes sont tels que l'axe des abscisses est dirigé vers le deuxième primaire, l'axe des ordonnées fait un angle de
des deux primaires et dont les axes sont tels que l'axe des abscisses est dirigé vers le deuxième primaire, l'axe des ordonnées fait un angle de 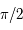 avec celui des abscisse dans le même sens que le mouvement de rotation des primaires, et l'axe des
avec celui des abscisse dans le même sens que le mouvement de rotation des primaires, et l'axe des 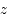 complète un trièdre direct.
complète un trièdre direct.
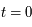 .
.
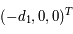 et
et 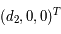 , où
, où 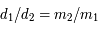 et
et 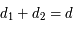 qui est la distance (fixe) qui sépare les deux primaires. On note
qui est la distance (fixe) qui sépare les deux primaires. On note 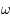 la vitesse de rotation angulaire des deux primaires par rapport au repère fixe.
la vitesse de rotation angulaire des deux primaires par rapport au repère fixe.
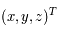 les coordonnées dans le repère fixe et
les coordonnées dans le repère fixe et 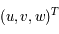 les coordonnées dans le repère tournant.
Le point au dessus d'une quantité indique la dérivée par rapport au temps de cette quantité.
les coordonnées dans le repère tournant.
Le point au dessus d'une quantité indique la dérivée par rapport au temps de cette quantité.
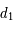 et
et 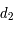 en fonction de
en fonction de 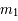 ,
, 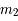 et
et 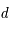 .
.
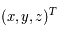 et
et 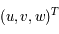 pour un même objet.
pour un même objet.
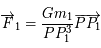 et
et 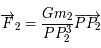 . En appliquant le principe fondamental de la dynamique, c'est-à-dire que l'accélération est égale à la somme des forces dans le repère fixe, écire les équations différentielles
vérifiées par les coordonnées
. En appliquant le principe fondamental de la dynamique, c'est-à-dire que l'accélération est égale à la somme des forces dans le repère fixe, écire les équations différentielles
vérifiées par les coordonnées 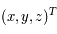 de
de  .
.
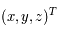 en fonction de
en fonction de 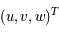 , en déduire les équations du mouvement dans le repère tournant.
, en déduire les équations du mouvement dans le repère tournant.
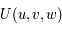 tel que le système d'équations précédent s'écrit :
tel que le système d'équations précédent s'écrit :
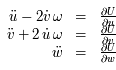 ,
,
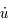 ,
, 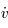 et
et 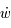 respectivement, puis en additionnant, montrer que le système admet une intégrale du mouvement (c'est -à-dire une quantité qui est constante au cours du temps).
respectivement, puis en additionnant, montrer que le système admet une intégrale du mouvement (c'est -à-dire une quantité qui est constante au cours du temps).
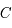 en fonction de
en fonction de 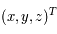 et de leur dérivées par rapport au temps.
et de leur dérivées par rapport au temps.
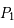 et
et 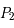 correspondent au Soleil et à Jupiter respectivement.
On pose
correspondent au Soleil et à Jupiter respectivement.
On pose 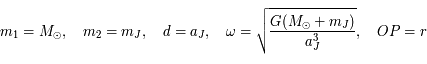 . Comme
. Comme  ,
on en déduit que
,
on en déduit que 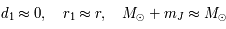 .
.
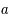 ,
, 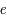 , et
, et 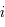 le demi-grand axe, l'excentricité et l'inclinaison de cette trajectoire. On a alors les relations suivantes:
le demi-grand axe, l'excentricité et l'inclinaison de cette trajectoire. On a alors les relations suivantes:
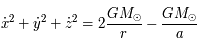 ,
, 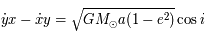 , réécrire l'équation précédente pour
, réécrire l'équation précédente pour  en fonction
de
en fonction
de 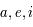 . L'expression obtenue correspond au paramètre de Tisserand qui est une quasi constante du mouvement pour les comètes
de la famille de Jupiter qui sont essentiellement soumisent à l'influence de Jupiter et du Soleil. On remarquera que les approximations faites
fonctionnent pourvu que l'on ne soit pas trop proche de Jupiter.
. L'expression obtenue correspond au paramètre de Tisserand qui est une quasi constante du mouvement pour les comètes
de la famille de Jupiter qui sont essentiellement soumisent à l'influence de Jupiter et du Soleil. On remarquera que les approximations faites
fonctionnent pourvu que l'on ne soit pas trop proche de Jupiter.
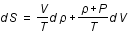
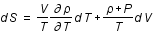
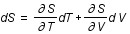
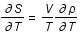 et
et 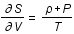 .
.
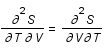 ,
, 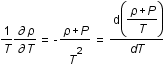
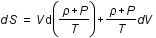 .
Donc,
.
Donc, 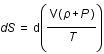 et
et 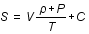 , où C est une constante d'intégration.
, où C est une constante d'intégration.
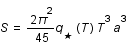
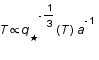 .
.
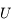 est tel que
est tel que 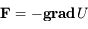 . Dans le repère polaire on a:
. Dans le repère polaire on a:
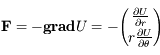 ,
,
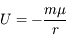 , en considérant que le potentiel est nul à l'infini.
L'énergie potentielle est donc:
, en considérant que le potentiel est nul à l'infini.
L'énergie potentielle est donc: 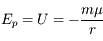 (on rappelle que la masse de
(on rappelle que la masse de 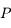 est égale à 1).
est égale à 1).
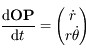 . Donc l'énergie cinétique est
. Donc l'énergie cinétique est 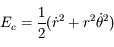 .
.
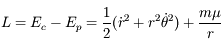 ,
,
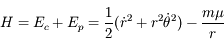 .
.
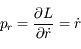 et
et 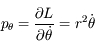
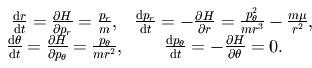
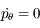 correspond à la loi des aires et découle du fait que
correspond à la loi des aires et découle du fait que 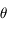 n'est pas présent explicitement dans le hamiltonien.
n'est pas présent explicitement dans le hamiltonien.
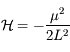 , ainsi les équations de hamilton nous donnent:
, ainsi les équations de hamilton nous donnent:
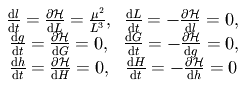 .
.
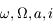 et
et 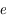 sont constants. Seule l'anomalie moyenne varie, et est donnée par
sont constants. Seule l'anomalie moyenne varie, et est donnée par 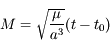 , où
, où 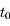 correspond au passage au péricentre, c'est à dire lorsque
correspond au passage au péricentre, c'est à dire lorsque 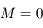 . Avec
. Avec 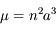 on retrouve bien la définition
on retrouve bien la définition 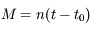 de l'anomalie moyenne donnée dans l'exercice sur l'
de l'anomalie moyenne donnée dans l'exercice sur l'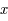 fixé et au voisinage de
fixé et au voisinage de 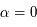 ,
, 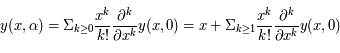
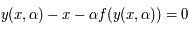 .
.
![\frac{\partial y}{\partial x} - 1 - \alpha \frac{\partial f}{\partial y} \frac{\partial y}{\partial x} = 0 \Longleftrightarrow \frac{\partial y}{\partial x} \Big{[} 1 - \alpha f'(y) \Big{]} = 1](../pages_der-part/equations_der-part/equation96.png) .
.
![\frac{\partial y}{\partial \alpha} - f(y(x,\alpha)) - \alpha \frac{\partial f}{\partial y} \frac{\partial y}{\partial \alpha} = 0 \Longleftrightarrow \frac{\partial y}{\partial \alpha} \Big{[} 1 - \alpha f'(y) \Big{]} = f(y)](../pages_der-part/equations_der-part/equation97.png) .
.
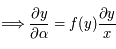 .
.
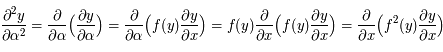 .
.
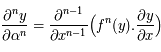 .
.
 ,
, 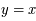 ,
, 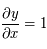 et
et 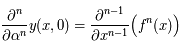 .
.
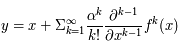 .
.
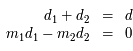 .
.
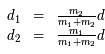 .
.
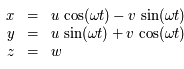 ,
,
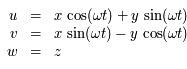 ,
,
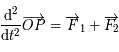 , soit :
, soit : 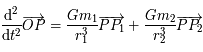 , où
, où 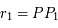 et
et 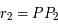 .
.
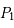 et
et 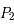 dans le repère fixe sont
dans le repère fixe sont 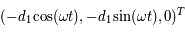 et
et 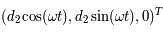 respectivement, on en déduit les équations du mouvement :
respectivement, on en déduit les équations du mouvement :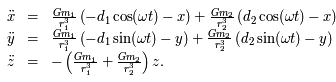
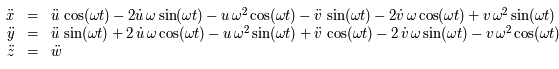 ,
,
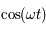 et la deuxième par
et la deuxième par 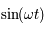 et en ajoutant d'une part, et en multipliant la première par
et en ajoutant d'une part, et en multipliant la première par
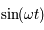 et la deuxième par
et la deuxième par 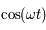 et en retranchant d'autre part, on obtient le système suivant :
et en retranchant d'autre part, on obtient le système suivant :
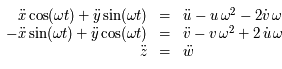 ,
,
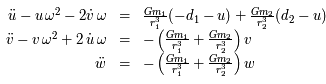 ,
,
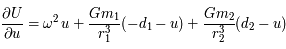 .
.
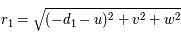 , ainsi
, ainsi 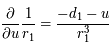 . De même
. De même 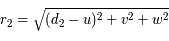 , ainsi
, ainsi 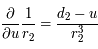 .
.
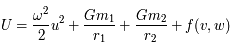 .
.
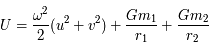 .
.
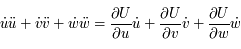 .
.
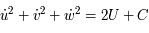 , où
, où 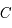 est une constante d'intégration.
est une constante d'intégration.
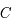 est une constante du mouvement.
est une constante du mouvement.
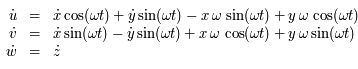
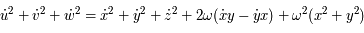 .
.
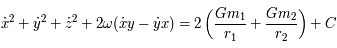
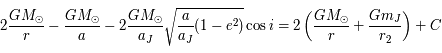 .
.
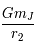 et avec
et avec 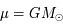 on obtient :
on obtient : 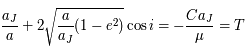 .
.