

Ex: paramètre de Tisserand |
Difficulté : ☆ Temps : 1h30
On considère un problème de trois corps où les deux premiers 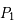 et
et 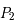 , appelés primaires et de masse respective
, appelés primaires et de masse respective 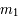 et
et 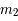 , sont sur des orbites circulaires et uniforme ; et le troisième
, sont sur des orbites circulaires et uniforme ; et le troisième 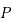 , de masse
négligeable voit sa trajectoire affectée
par les primaires alors que celui-ci n'affecte pas le mouvement des deux primaires. Ce problème est appelé le problème de trois corps restreint et circulaire.
, de masse
négligeable voit sa trajectoire affectée
par les primaires alors que celui-ci n'affecte pas le mouvement des deux primaires. Ce problème est appelé le problème de trois corps restreint et circulaire.
On considère un repère tournant orthonormé, centré sur le centre de gravité 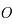 des deux primaires et dont les axes sont tels que l'axe des abscisses est dirigé vers le deuxième primaire, l'axe des ordonnées fait un angle de
des deux primaires et dont les axes sont tels que l'axe des abscisses est dirigé vers le deuxième primaire, l'axe des ordonnées fait un angle de 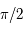 avec celui des abscisse dans le même sens que le mouvement de rotation des primaires, et l'axe des
avec celui des abscisse dans le même sens que le mouvement de rotation des primaires, et l'axe des 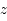 complète un trièdre direct.
complète un trièdre direct.
On considère aussi un repère fixe orthonormé qui coïncide avec le repère tournant à 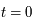 .
.
Dans le repère tournant, les coordonnées des deux primaires sont 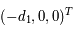 et
et 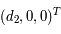 , où
, où 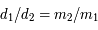 et
et 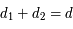 qui est la distance (fixe) qui sépare les deux primaires. On note
qui est la distance (fixe) qui sépare les deux primaires. On note 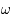 la vitesse de rotation angulaire des deux primaires par rapport au repère fixe.
la vitesse de rotation angulaire des deux primaires par rapport au repère fixe.
De manière générale on notera 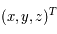 les coordonnées dans le repère fixe et
les coordonnées dans le repère fixe et 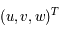 les coordonnées dans le repère tournant.
Le point au dessus d'une quantité indique la dérivée par rapport au temps de cette quantité.
les coordonnées dans le repère tournant.
Le point au dessus d'une quantité indique la dérivée par rapport au temps de cette quantité.
Exprimer 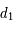 et
et 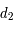 en fonction de
en fonction de 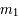 ,
, 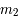 et
et 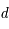 .
.
Déterminer les formules de passage entre 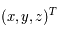 et
et 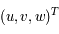 pour un même objet.
pour un même objet.
Les deux forces qui s'appliquent au troisième corps sont 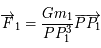 et
et 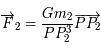 . En appliquant le principe fondamental de la dynamique, c'est-à-dire que l'accélération est égale à la somme des forces dans le repère fixe, écire les équations différentielles
vérifiées par les coordonnées
. En appliquant le principe fondamental de la dynamique, c'est-à-dire que l'accélération est égale à la somme des forces dans le repère fixe, écire les équations différentielles
vérifiées par les coordonnées 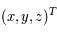 de
de 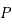 .
.
En différenciant les expressions de 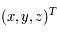 en fonction de
en fonction de 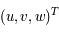 , en déduire les équations du mouvement dans le repère tournant.
, en déduire les équations du mouvement dans le repère tournant.
Montrer qu'il existe une fonction 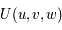 tel que le système d'équations précédent s'écrit :
tel que le système d'équations précédent s'écrit :
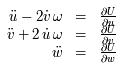 ,
,
En multipliant chaque ligne du système précédent par 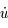 ,
, 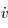 et
et 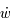 respectivement, puis en additionnant, montrer que le système admet une intégrale du mouvement (c'est -à-dire une quantité qui est constante au cours du temps).
respectivement, puis en additionnant, montrer que le système admet une intégrale du mouvement (c'est -à-dire une quantité qui est constante au cours du temps).
En déduire 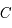 en fonction de
en fonction de 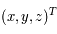 et de leur dérivées par rapport au temps.
et de leur dérivées par rapport au temps.
On considère maintenant que les deux primaires 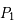 et
et 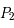 correspondent au Soleil et à Jupiter respectivement.
On pose
correspondent au Soleil et à Jupiter respectivement.
On pose 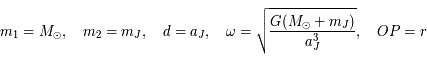 . Comme
. Comme 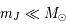 ,
on en déduit que
,
on en déduit que 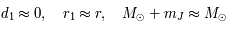 .
.
On peut alors considérer la trajectoire du troisième comme une orbite keplerienne autour du Soleil se trouvant à l'origine.
Soit 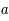 ,
, 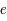 , et
, et 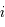 le demi-grand axe, l'excentricité et l'inclinaison de cette trajectoire. On a alors les relations suivantes:
le demi-grand axe, l'excentricité et l'inclinaison de cette trajectoire. On a alors les relations suivantes:
Sachant que 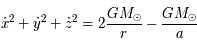 ,
, 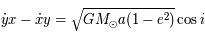 , réécrire l'équation précédente pour
, réécrire l'équation précédente pour 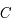 en fonction
de
en fonction
de 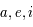 . L'expression obtenue correspond au paramètre de Tisserand qui est une quasi constante du mouvement pour les comètes
de la famille de Jupiter qui sont essentiellement soumisent à l'influence de Jupiter et du Soleil. On remarquera que les approximations faites
fonctionnent pourvu que l'on ne soit pas trop proche de Jupiter.
. L'expression obtenue correspond au paramètre de Tisserand qui est une quasi constante du mouvement pour les comètes
de la famille de Jupiter qui sont essentiellement soumisent à l'influence de Jupiter et du Soleil. On remarquera que les approximations faites
fonctionnent pourvu que l'on ne soit pas trop proche de Jupiter.