images/logos_obspm_lille1.png

L'Astronomie dans l'apprentissage des Mathématiques

L'Astronomie dans l'apprentissage des Mathématiques

Fonctions de plusieurs variables

Dérivations partielles

• Ex: Entropie

• Formulation hamiltonienne du problème de 2 corps

• Ex: Formulation hamiltonienne du problème de 2 corps

• Les variables de Delaunay

• Ex: les variables de Delaunay

• Théorème d'inversion de Lagrange

• Ex: Théorème d'inversion de Lagrange

• Paramètre de Tisserand

• Ex: paramètre de Tisserand

Ex: les variables de Delaunay

Auteurs: Jérôme Thiébaut, Marc Fouchard, S. Renner

Auteur: Marc Fouchard

Les variables de Delaunay

Difficulté : ☆ Temps : 10 mn

Question 1)

Les variables de Delaunay sont les coordonnées 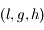(l,g,h) associées aux moments conjuguées 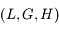(L,G,H) (voir ce cours de mécanique céleste ainsi que l' exercice précédent) avec:

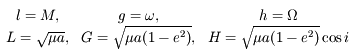$\begin{array}{ccc} l=M, & g=\omega, & h=\Omega \\ L=\sqrt{\mu a}, & G=\sqrt{\mu a (1-e^2)}, & H=\sqrt{\mu a (1-e^2)}\cos i \end{array}$ .

où 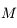est l'anomalie moyenne, 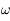$\omega$ est l'argument du péricentre, 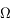$\Omega$ est la longitude du noeud ascendant, 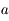est le demi-grand axe, 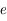est l'excentricité et est l'inclinaison.

Sachant que le hamiltonien du problème de deux corps (où on a supposé ici que le corps massif était de masse unité) est: 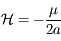$\mathcal H=-\frac{\mu}{2a}$ , (voir cet exercice sur l'équation de Kepler) en déduire les équations de Hamilton et résoudre le système.