images/logos_obspm_lille1.png

L'Astronomie dans l'apprentissage des Mathématiques

L'Astronomie dans l'apprentissage des Mathématiques

Fonctions de plusieurs variables

Dérivations partielles

• Ex: Entropie

• Formulation hamiltonienne du problème de 2 corps

• Ex: Formulation hamiltonienne du problème de 2 corps

• Les variables de Delaunay

• Ex: les variables de Delaunay

• Théorème d'inversion de Lagrange

• Ex: Théorème d'inversion de Lagrange

• Paramètre de Tisserand

• Ex: paramètre de Tisserand

Ex: Théorème d'inversion de Lagrange

Auteurs: Jérôme Thiébaut, Marc Fouchard, S. Renner

Auteur: S. Renner

Théorème d'inversion de Lagrange

Difficulté : ☆☆ Temps : 1H

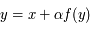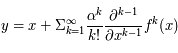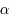On va donc démontrer que si $y = x + \alpha f(y)$ , alors $\displyastyle y = x + \Sigma_{k=1}^\infty \frac{\alpha^k}{k!} \frac{\partial^{k-1}}{\partial x^{k-1}} f^k(x)$ avec $\alpha$ petit.

Question 1)

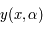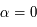Développer $y(x,\alpha)$ au voisinage de $\alpha = 0$ .

Question 2)

Montrer que 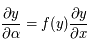$\frac{\partial y}{\partial \alpha} = f(y) \frac{\partial y}{\partial x}$ .

Question 3)

Montrer que pour tout entier 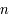strictement positif, 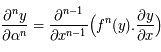$\displaystyle \frac{\partial^n y}{\partial \alpha^n} = \frac{\partial^{n-1}}{\partial x^{n-1}} \Big{(} f^n(y). \frac{\partial y}{\partial x}\Big{)}$ . On utilisera le résultat de la question précédente.

Question 4)

En déduire 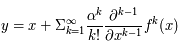$\displyastyle y = x + \Sigma_{k=1}^\infty \frac{\alpha^k}{k!} \frac{\partial^{k-1}}{\partial x^{k-1}} f^k(x)$ .