Ex: Entropie

Auteurs: Jérôme Thiébaut, Marc Fouchard, S. Renner

Auteur: Jérôme Thiébaut

Entropie

Difficulté : ☆ Temps : 10 min

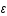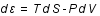On peut relier la variation d'énergie, epsilon , aux variations d'entropie, S, et de volume, V, par la relation suivante: d*epsilon=T*d*S-P*d*V , où T est la température et P la pression.

Question 1)

Exprimer la variation d'entropie en fonction des variations de volume et de densité volumique d'énergie, 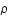rho .

Aide Solution

Question 2)

Exprimer la variation d'entropie en fonction des variations de volume et de température.

Aide Solution

Question 3)

Montrer que (1/T)*(drond*rho/drond*T)=d((rho+P)/T)/dT .

Aide Solution

Question 4)

Exprimer la variation d'entropie comme la variaton d'une seule quantité dépendant de V, P, T et 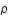rho puis relier l'entropie à ces variables thermodynamiques.

Solution

Question 5)

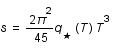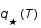D'autres calculs thermodynamiques montrent que la densité d'entropie $s=frac(2*pi^2;45)*q_(star)*((T))*T^3$ , où q_star*((T)) est un facteur dépendant de la température et des particules présentes. L'unité de volume est 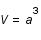V=a^3 , où 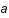est le facteur d'échelle mesurant l'expansion de l'univers. Exprimer S comme une fonction de la température T et du facteur d'échelle a.

Solution