Auteur : Marc Fouchard
Le mouvement de Mars vu depuis la Terre montre des périodes pendant lesquelles Mars se déplace dans le sens inverse au
Soleil par rapport au fond d'étoiles fixes. L'exercice présenté ici consiste à étudier cette phase de rétrogradation de Mars.
L'animation ci-dessous montre à gauche le mouvement de la Terre et de Mars autour du Soleil et à droite les mêmes mouvements vus depuis la Terre.
Retrogradation de Mars
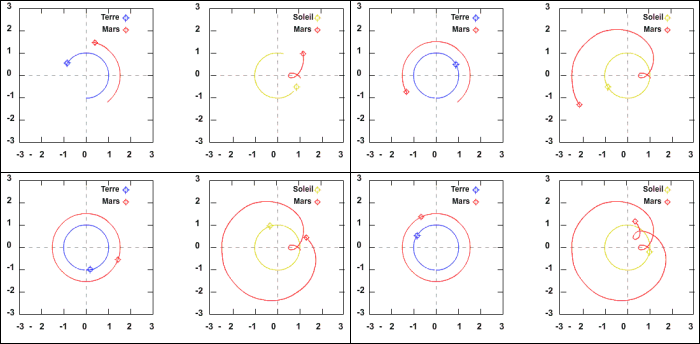
Mouvement de la Terre et de Mars autour du Soleil.
On remarque que vu de la Terre le mouvement de Mars se fait dans le sens inverse (sens retrograde) à celui du Soleil (sens prograde). Le but de cet exercice est d'étudier cette phase de rétrogradation.
Auteur: S. Renner
Date de création: 04 avril 2011
L'objectif de cet exercice est de déterminer quels types de forces perturbatrices peuvent modifier le demi grand-axe ou l'excentricité d'une orbite.
Il est nécessaire de s'intéresser au préalable à la résolution du problème à 2 corps.
Auteur: Stéphane Erard
Date de création: 07 mars 2013
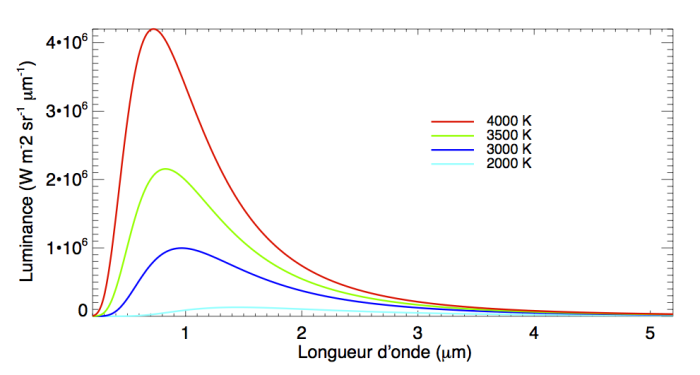
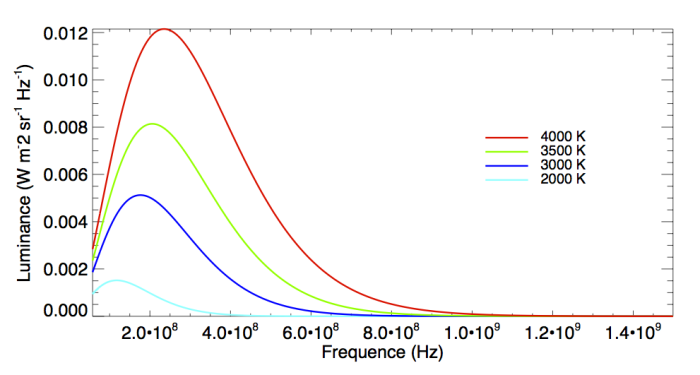
La loi de Planck donnant le spectre du corps noir est souvent donnée en fonction de la longueur d'onde. L'objectif de cet exercice est de dériver cette loi en fonction de la fréquence du rayonnement. Cette expression est plus naturellement utilisée dans certains domaines, en particulier aux basses énergies (domaine radio) et aux basses températures (dans le milieu interstellaire par exemple).
Auteur: Stéphane Erard
 Loi de Planck en fréquence
Loi de Planck en fréquence
Difficulté : ☆
Temps : 30 min
On connaît la luminance du corps noir en fonction de la longueur d'onde, donnée par la loi de Planck (voir par exemple l'exercice sur la loi de Wien) :
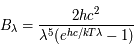
où 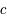 est la vitesse de la lumière dans le vide,
est la vitesse de la lumière dans le vide, 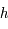 la constante de Planck,
la constante de Planck, 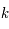 la constante de Boltzmann,
la constante de Boltzmann, 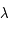 la longueur d'onde et
la longueur d'onde et 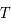 la température du corps noir.
la température du corps noir.
Cette expression est une luminance directionnelle, donnée habituellement en 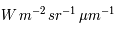 .
.
Question 1)
Donner l'expression de cette luminance en fonction de la fréquence du rayonnement.
Longueur d'onde et fréquence d'un rayonnement sont reliés par 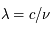
où c est la vitesse de la lumière dans le vide.
Question 2)
Comparer les graphiques de ces deux expressions en échelle linéaire.
-
Question 1
Solution :
Pour la Terre on a :
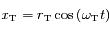
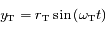 .
.
Et pour Mars on a :
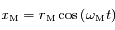
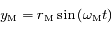 .
.
On en déduit :
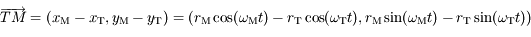 .
.
On en déduit:
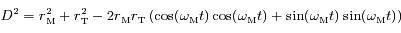
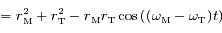 ,
,
et
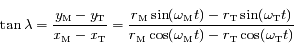 . Cette fonction n'est pas définie lorsque
. Cette fonction n'est pas définie lorsque 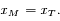
-
Question 2
Solution :
On a:
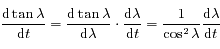 .
.
Or
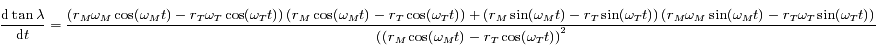
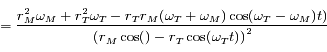 .
.
Le signe de 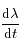 est celui du numérateur de l'expression ci-dessus.
Ainsi, quand
est celui du numérateur de l'expression ci-dessus.
Ainsi, quand 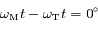 , le signe de la dérivée est celui de
, le signe de la dérivée est celui de 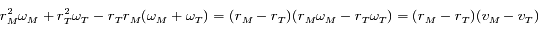 ,
oùt
,
oùt 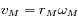 et
et 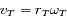 .
.
Or d'après la propriété dérivant de la troisième loi de Kepler, on a
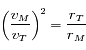 . Ainsi, pour Mars on a
. Ainsi, pour Mars on a 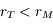 et
et 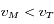 , donc la dérivée est négative.
De même on montre que pour
, donc la dérivée est négative.
De même on montre que pour 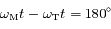 , la dérivée est positive.
, la dérivée est positive.
On en conclue qu'effectivement lors de l'opposition ( 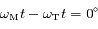 ), le mouvement de Mars est rétrograde, alors qu'à la conjonction
), le mouvement de Mars est rétrograde, alors qu'à la conjonction 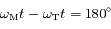 , le mouvement est prograde.
, le mouvement est prograde.
-
Question 3
Solution :
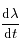 s'annulle lorsque
s'annulle lorsque 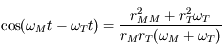 , soit
, soit 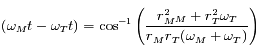 .
.
Ce qui nous donne, à 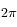 près, deux solutions opposées l'une de l'autre.
près, deux solutions opposées l'une de l'autre.
-
Question 4
Solution :
On a 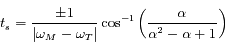 , d'où la durée de la rétrogradation
, d'où la durée de la rétrogradation 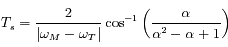 .
.
Pour Mars, cette durée est égale à 72,8 jours.

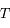 et Mars
et Mars 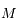 se déplacent
se déplacent 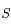 . Soit
. Soit 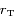 et
et 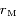 les rayons respectives des
les rayons respectives des 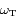 ,
, 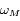 leur
leur 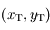 et
et 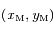 les coordonnées respectives de la Terre et de Mars. On suppose qu'initialement le Soleil, la Terre et Mars sont alignés dans cet ordre sur l'axe des abscisses du côté des abscisses positives.
les coordonnées respectives de la Terre et de Mars. On suppose qu'initialement le Soleil, la Terre et Mars sont alignés dans cet ordre sur l'axe des abscisses du côté des abscisses positives.
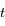 . Soit
. Soit 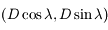 les coordonnées du vecteur
les coordonnées du vecteur 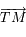 . En déduire une expression de
. En déduire une expression de 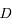 et de
et de 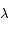 en fonction de
en fonction de 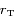 ,
, 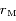 ,
, 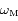 ,
, 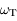 et
et 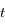 .
.
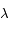 par rapport au temps, puis déterminer son signe pour
par rapport au temps, puis déterminer son signe pour 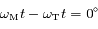 et
et 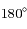 .
On utilisera la propriété
.
On utilisera la propriété 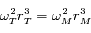 qui dérive de la troisième loi de Kepler.
Conclure.
qui dérive de la troisième loi de Kepler.
Conclure.
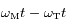 lorsque
lorsque 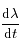 s'annule. Ces positions correspondent aux stations de Mars. On notera dans la suite
s'annule. Ces positions correspondent aux stations de Mars. On notera dans la suite 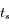 un instant conrrespondant à une station.
un instant conrrespondant à une station.
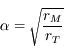 . En déduire la durée de la rétrogradation.
. En déduire la durée de la rétrogradation.
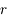 ) est soumis à une force perturbatrice de la forme
) est soumis à une force perturbatrice de la forme 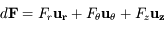 , où
, où 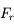 ,
, 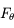 ,
, 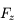 sont respectivement les composantes (constantes) radiale, tangentielle et normale de la force, et
sont respectivement les composantes (constantes) radiale, tangentielle et normale de la force, et 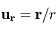 ,
, 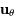 ,
, 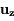 des vecteurs orthonormés unitaires. Cette force est suffisamment faible pour que la trajectoire de l'objet reste keplerienne.
des vecteurs orthonormés unitaires. Cette force est suffisamment faible pour que la trajectoire de l'objet reste keplerienne.
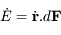 due à la force
due à la force 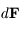 . Sachant de plus que
. Sachant de plus que 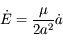 avec
avec 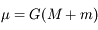 , montrer quels types de forces vont modifier le
, montrer quels types de forces vont modifier le 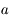 en calculant
en calculant 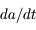 .
.
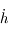 due à
due à 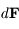 , montrer quels types de forces modifient l'
, montrer quels types de forces modifient l'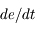 .
.
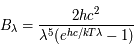
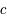 est la vitesse de la lumière dans le vide,
est la vitesse de la lumière dans le vide, 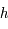 la constante de Planck,
la constante de Planck, 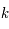 la constante de Boltzmann,
la constante de Boltzmann, 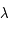 la longueur d'onde et
la longueur d'onde et 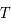 la température du corps noir.
la température du corps noir.
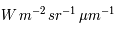 .
.
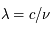
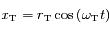
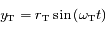 .
.
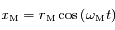
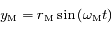 .
.
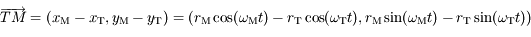 .
.
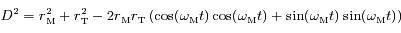
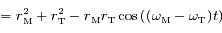 ,
,
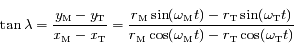 . Cette fonction n'est pas définie lorsque
. Cette fonction n'est pas définie lorsque 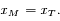
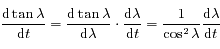 .
.
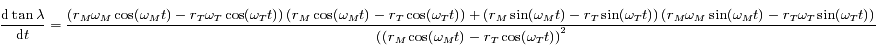
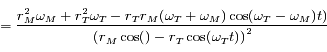 .
.
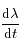 est celui du numérateur de l'expression ci-dessus.
Ainsi, quand
est celui du numérateur de l'expression ci-dessus.
Ainsi, quand 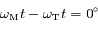 , le signe de la dérivée est celui de
, le signe de la dérivée est celui de 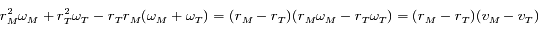 ,
oùt
,
oùt 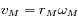 et
et 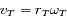 .
.
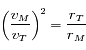 . Ainsi, pour Mars on a
. Ainsi, pour Mars on a 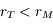 et
et 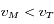 , donc la dérivée est négative.
De même on montre que pour
, donc la dérivée est négative.
De même on montre que pour 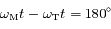 , la dérivée est positive.
, la dérivée est positive.
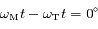 ), le mouvement de Mars est rétrograde, alors qu'à la
), le mouvement de Mars est rétrograde, alors qu'à la 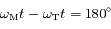 , le mouvement est prograde.
, le mouvement est prograde.
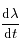 s'annulle lorsque
s'annulle lorsque 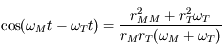 , soit
, soit 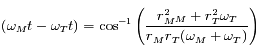 .
.
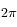 près, deux solutions opposées l'une de l'autre.
près, deux solutions opposées l'une de l'autre.
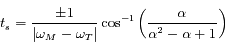 , d'où la durée de la rétrogradation
, d'où la durée de la rétrogradation 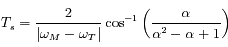 .
.
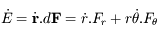 et
et 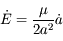 , où
, où 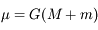 .
.
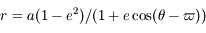 ,
, 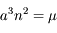 donc
donc 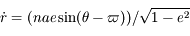 et
et ![r {\dot \theta} = (na [1 + e \cos(\theta - \varpi) ]) / \sqrt{1 - e^2}](../pages_def/equations_def/equation77.png) .
.
![{\dot a} = 2 a^{\displaystyle 3/2} [F_r e \sin (\theta - \varpi) + F_\theta (1 + e \cos (\theta - \varpi)) ]/\sqrt{\mu(1-e^2)}](../pages_def/equations_def/equation78.png)
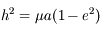 ,
, 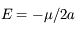 , donc
, donc 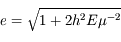 et
et 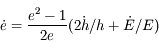 .
.
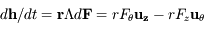 donc
donc 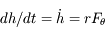
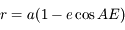 où
où 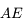 est l'
est l'![{\dot e} = \sqrt{a(1-e^2)/\mu}[F_r \sin(\theta - \varpi) + F_\theta (\cos (\theta-\varpi) + \cos AE]](../pages_def/equations_def/equation90.png) .
.
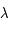 et
et 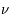 sont égales, elles donnent toutes deux la luminance intégrale du corps noir (
sont égales, elles donnent toutes deux la luminance intégrale du corps noir (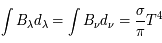
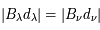 où
où 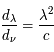
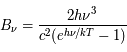 (donné couramment en
(donné couramment en 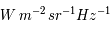 )
)