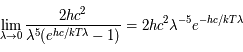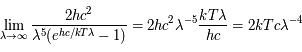On trouvera dans ce chapitre les exercices suivants :
- Détermination du rayon d'Einstein pour les lentilles gravitationnelles
- Une application en lien avec le passage des coordonnées horizontales aux coordonnées horaires (angle horaire et déclinaison)
- Résolution de l'équation de Kepler dans le cas elliptique par utilisation de formule de Taylor
- Estimation de la limite de Roche
- Les expressions du corps noir à longues et courtes longueurs d'onde
Auteur : Jérôme Thiébaut
L'idée de base de la relativité générale est que la matière, par sa masse, courbe l'espace. Ainsi, une planète orbitant autour d'une étoile n'est pas soumise à une force de gravitation mais circule librement sur un espace courbé par l'étoile. Il s'ensuit que la lumière, bien que dépourvue de masse, est également déviée par la présence d'un corps massif.
Si un corps massif se situe entre une galaxie lointaine et un observateur, celui ci va donc dévier la lumière de la galaxie et déformer son image. C'est ce qu'on appelle une lentille gravitationnelle. Dans le cas où les trois objets sont parfaitement alignés, l'image de la galaxie se déforme pour former un anneau autour de la lentille appelé anneau d'Einstein.
Le but de cet exercice est de déterminer le diamètre angulaire de cet anneau en fonction des caractéristiques du système (masse et distances).
Lentille Gravitationnelle

Lentille gravitationnelle : la déviation de la lumière par un fort potentiel gravitationnel (l'amas de galaxies 0024+1654) conduit à de multiples images d'un objet situé derrière le centre de masse du déflecteur.
Crédit :
HST
Auteur: Jérôme Thiébaut
 Lentille gravitationnelle
Lentille gravitationnelle
Difficulté : ☆
Temps : 30 min
La figure montre le schéma du principe d'une lentille gravitationnelle. La source, S, est déviée par la lentille, L, et son image, I, est donc vue par l'observateur, O, selon un angle 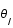 au lieu de
au lieu de  .
.
Principe d'une lentille gravitationnelle
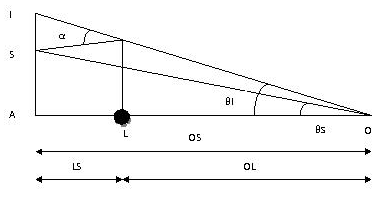
Crédit :
Jérôme Thiébaut
Question 1)
Exprimer les distances AS et AI en fonction des angles 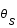 et
et 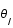 et de la distance OS.
et de la distance OS.
Question 3)
Dans le cas où la source, la lentille et l'observateur sont parfaitement alignés, déterminer le rayon angulaire (rayon d'Einstein) sous lequel sera vu la source toujours en fonction des grandeurs caractéristiques du système.
Dans le cas d'un alignement, 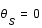 .
.
Auteur : S. Renner
Date de création: 30 novembre 2009
On propose ici un exercice en lien avec le passage des coordonnées locales (ou horizontales) aux coordonnées horaires (angle horaire et déclinaison).
Il est donc préférable de se familiariser avec les systèmes de coordonnées utilisés en astronomie pour le repérage des étoiles dans le ciel, ainsi qu'avec les formules de base de la trigonométrie sphérique.
Auteur: S. Renner
 Repérage des astres
Repérage des astres
Difficulté : ☆☆
Temps : 1h
Dans le triangle sphérique PZM (voir la fiche de résolution du triangle sphérique), on obtient des relations qui permettent de passer des coordonnées horizontales aux coordonnées horaires, et inversement.
Question 2)
En déduire qu'au voisinage du passage au méridien d'un astre, sa distance zénithale 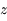 varie comme le carré de l'angle horaire (en se limitant au 2ème ordre).
varie comme le carré de l'angle horaire (en se limitant au 2ème ordre).
Auteur : Marc Fouchard
Dans le problème de deux corps (voir cet exercice), on sait que le déplacement d'un corps par rapport à l'autre se fait sur une conique dont le deuxième corps occupe l'un des foyers (voir aussi cet . Une fois la conique fixée il ne reste alors qu'à positionner le corps sur son orbite. Pour cela on utilise une quantité qu'on appelle anomalie. On définie trois types d'anomalie: l'anomalie moyenne, l'anomalie vraie et l'anomalie excentrique.
Les trois anomalies
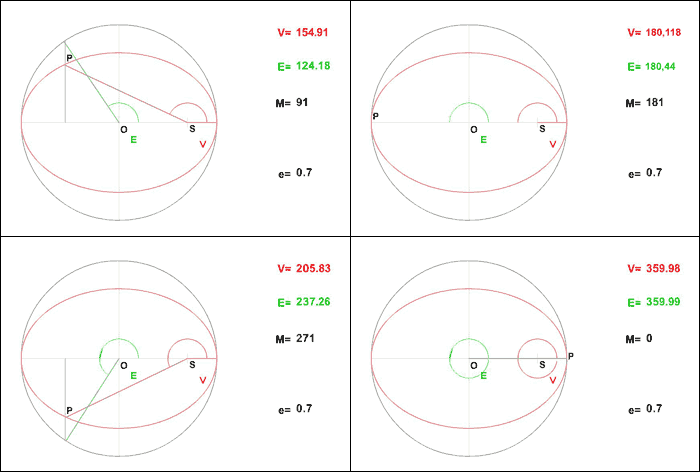
L'animation ci-dessus montre le lien entre les 3 anomalies. Comme on peut le voir,
l'anomalie moyenne correspond en fait à un temps. Il n'existe pas de relation géométrique entre l'anomalie moyenne et les autres anomalies. En revanche, il existe une relation (voir cet exercice), appelée équation de Kepler, qui relie l'anomalie moyenne à l'anomalie excentrique. Cette relation est:
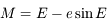 ,
,
où 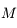 est l'anomalie moyenne,
est l'anomalie moyenne, 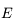 l'anomalie excentrique et
l'anomalie excentrique et 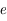 l'excentricité de la trajectoire.
l'excentricité de la trajectoire.
On voit que connaissant 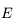 il est facile d'avoir
il est facile d'avoir 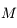 , mais en revanche connaissant
, mais en revanche connaissant 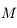 il n'est pas possible d'avoir
il n'est pas possible d'avoir 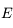 sous forme analytique. L'objet de cette exercice est justement de déterminer un algorithme puissant d'inversion de cette équation.
sous forme analytique. L'objet de cette exercice est justement de déterminer un algorithme puissant d'inversion de cette équation.
Auteur: Marc Fouchard
 Equation de Kepler
Equation de Kepler
Difficulté : ☆☆
Temps : 1h30
Question 3)
Montrer que:
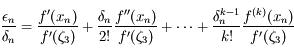 , avec
, avec 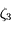 un nombre entre
un nombre entre 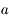 et
et 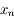 .
.
Question 4)
En déduire que 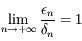 .
.
Question 6)
Il nous faut maintenant calculer la solution 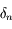 de l'équation qui le défini. Avant tout, jusitfier pourquoi il suffit d'avoir une solution approxée à
de l'équation qui le défini. Avant tout, jusitfier pourquoi il suffit d'avoir une solution approxée à 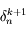 près.
près.
Question 7)
Montrer que pour 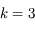 , on a:
, on a:
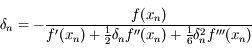
Question 8)
Montrer qu'en utilisant la séquance suivante:
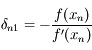 ,
,
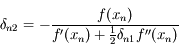 ,
,
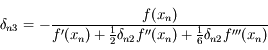 ,
,
on obtient une approximation de 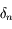 à
à 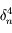 près. On pourra procéder par étape en montrant que
près. On pourra procéder par étape en montrant que 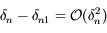 , puis que
, puis que 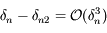 et enfin que
et enfin que 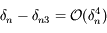 .
.
Question 9)
Montrer que l'on peut appliquer l'algorithme précédent pour inverser l'équation de Kepler sur l'intervalle ![[0,2\pi]](../pages_dl/equations_dl/equation149.png) . Aplliquer l'algorithme à quelque exemple et remarquer qu'on obtient une erreur inférieure à
. Aplliquer l'algorithme à quelque exemple et remarquer qu'on obtient une erreur inférieure à 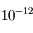 en moins de 4 itérations.
en moins de 4 itérations.
Auteur : S. Renner
Date de création: 31 janvier 2011
On cherche à déterminer la distance, que l'on notera 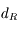 , en dessous de laquelle un satellite commence à se disloquer sous l'action des forces de marée causées par la planète autour de laquelle il orbite.
, en dessous de laquelle un satellite commence à se disloquer sous l'action des forces de marée causées par la planète autour de laquelle il orbite.
Cette distance théorique s'appelle la limite de Roche. Elle tire son nom de l'astronome français qui l'a formulée en 1850.
Auteur: S. Renner
 Effet de marée et limite de Roche
Effet de marée et limite de Roche
Difficulté : ☆☆
Temps : 1h
On se place dans un référentiel galiléen centré sur la planète, supposée sphérique, homogène, de masse 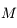 , rayon
, rayon 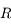 , et masse volumique
, et masse volumique 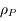 .
.
On suppose que le satellite est constitué de deux sphères homogènes identiques (de masse 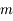 , de rayon
, de rayon 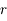 et de masse volumique
et de masse volumique 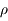 ), et qu'il est en orbite circulaire de rayon
), et qu'il est en orbite circulaire de rayon 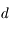 autour de la planète.
autour de la planète.
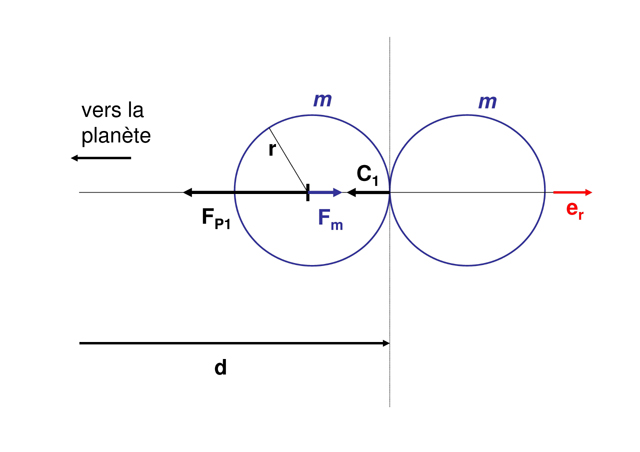
Bilan des forces agissant sur une masse
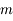
dans le repère lié à la planète (supposé galiléen) :
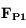
est la force d'attraction gravitationnelle de la planète,
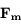
celle de la deuxième sphère de masse
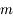
,
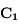
la force de contact entre les deux sphères.
Question 1)
En appliquant le principe fondamental de la dynamique (PFD) au système des deux masses 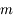 , montrer qu'au premier ordre en
, montrer qu'au premier ordre en 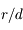 la vitesse
angulaire de la comète est
la vitesse
angulaire de la comète est 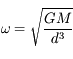 .
.
Question 2)
Appliquer le PFD à l'une des masses 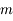 , et trouver un critère de fragmentation du satellite (contact rompu entre les deux sphères) au premier ordre en
, et trouver un critère de fragmentation du satellite (contact rompu entre les deux sphères) au premier ordre en 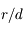 .
.
Question 4)
Retrouver l'expression de la limite de Roche en écrivant que la différence de force entre les deux masses 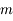 due à l'attraction gravitationnelle de la planète est supérieure à la force de gravitation mutuelle entre les deux sphères.
due à l'attraction gravitationnelle de la planète est supérieure à la force de gravitation mutuelle entre les deux sphères.
Auteur : Marc Fouchard
Date de création: 8 Mai 2013
En astronomie on a souvent besoin de reproduire le mouvement des objets en effectuant des intégraitons numériques. Quelque soit la méthode, elle repose toujours sur des approximations et elle nécessite un certain temps de calcul. Ainsi l'objectif d'une méthode est de trouver le meilleur compromis entre temps de calcul et précision.
Une méthode très performante est la méthode dite de Taylor.
Soit l'équation différentielle suivante :
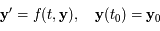 .
.
Soit 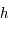 , un pas d'intégration. Le but est de trouver
, un pas d'intégration. Le but est de trouver 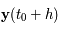 avec la meilleure précision possible.
avec la meilleure précision possible.
La méthode de Taylor repose sur le développement de 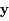 en
en 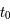 :
:
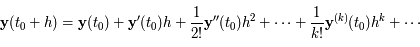
Le problème principal est donc d'estimer les coefficients du développement de Taylor de la solution.
Auteur: Marc Fouchard
 Générateur de coefficients de Taylor
Générateur de coefficients de Taylor
Difficulté : ☆☆
Temps : 30mn
Question 2)
Déterminer 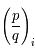 .
.
Question 3)
Montrer que :
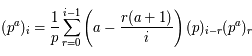
On pourra développer de deux manière différentes 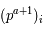
Auteur : Stéphane Erard
Date de création: 30 Mai 2013
La loi de Planck donne l'expression exacte du spectre du corps noir. Historiquement elle a été dérivée après des approximations valables aux grandes et courtes longueurs d'onde, qui sont toujours utilisées dans certaines situations. L'exercice propose de retrouver ces approximations à partir de la loi complète.
Auteur: Stéphane Erard
 Limites de la loi de Plack
Limites de la loi de Plack
Difficulté : ☆
Temps : 30 min
On connaît la luminance du corps noir en fonction de la longueur d'onde, donnée par la loi de Planck (voir par exemple l'exercice sur la loi de Wien) :
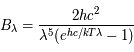
où 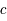 est la vitesse de la lumière dans le vide,
est la vitesse de la lumière dans le vide, 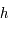 la constante de Planck,
la constante de Planck, 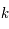 la constante de Boltzmann,
la constante de Boltzmann, 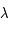 la longueur d'onde et
la longueur d'onde et 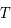 la température du corps noir.
la température du corps noir.
Cette expression donne la luminance directionnelle, en 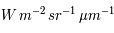 , du corps noir à toutes les longueurs d'onde.
, du corps noir à toutes les longueurs d'onde.
Question 1)
Donner une expression de cette loi à courtes longueurs d'onde. Cette expression est connue sous le nom de loi ou distribution de Wien.
Question 2)
Donner une expression de cette loi à grandes longueurs d'onde. Cette expression est connue sous le nom de loi de Rayleigh-Jeans. Commentaire ?
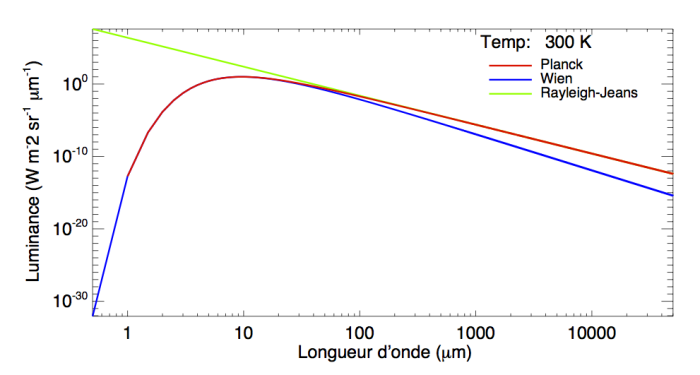
Question 3)
Tracer les graphiques de ces deux expressions et de la loi de Planck en échelle log/log, comparer. Quel problème pose l'approximation de Rayleigh-Jeans ?
-
Question 1
Solution :
On a, d'après la formule de Taylor avec reste, 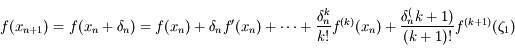 , avec
, avec 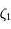 compris entre
compris entre 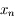 et
et 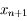 . D'après la définition de
. D'après la définition de 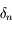 , on obtient:
, on obtient: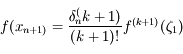 .
.
-
Question 2
Solution :
On a 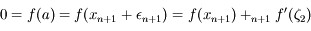 , avec
, avec 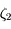 un nombre entre
un nombre entre 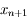 et
et 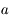 .
En combinant avec l'expression de
.
En combinant avec l'expression de 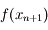 obtenue précédemment, et sachant que d'après nos hypothèses
obtenue précédemment, et sachant que d'après nos hypothèses 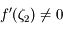 , on obtient:
, on obtient:
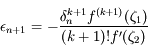 .
.
-
Question 3
Solution :
On a 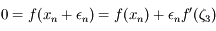 avec
avec 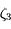 compris entre
compris entre 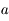 et
et 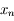 .
En remplaçant
.
En remplaçant 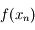 par
par 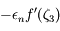 dans l'équation définissant
dans l'équation définissant 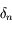 et en divisant par
et en divisant par 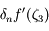 (ce que l'on peut faire puisque, d'après nos hypothèses,
(ce que l'on peut faire puisque, d'après nos hypothèses, 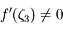 ) on obtient l'expression voulue.
) on obtient l'expression voulue.
-
Question 4
Solution :
On sait par hypothèse que 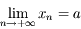 . Donc d'après la définition de
. Donc d'après la définition de 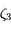 , on a aussi
, on a aussi 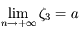 . Comme
. Comme 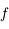 est de classe
est de classe 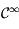 sur
sur 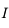 , sa dérivée première est continue, donc
, sa dérivée première est continue, donc 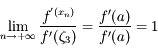 . Dautre part on a
. Dautre part on a 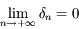 donc, d'après l'expression obtenue précedemment pour
donc, d'après l'expression obtenue précedemment pour 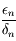 , on a bien la limite demandée.
, on a bien la limite demandée.
-
Question 5
Solution :
On a:
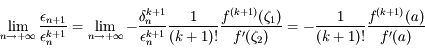 .
.
La première égalité vient de l'expression de 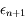 en fonction de
en fonction de 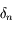 calculée prcédemment et la deuxième découle de la continuité des dérivées successives de
calculée prcédemment et la deuxième découle de la continuité des dérivées successives de 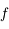 et de la définition de
et de la définition de 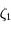 et
et 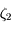 .
.
La conlusion découle de la définition de la convergence à l'ordre 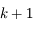 .
.
-
Question 6
Solution :
En effectuant la différence entre les deux équations définissant 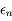 et
et 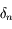 on a:
on a:
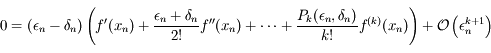 ,
,
avec 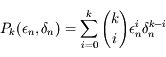 . Comme on a vu que
. Comme on a vu que 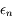 et
et 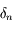 sont équivalents, on a bien:
sont équivalents, on a bien:
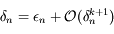 ,
,
ainsi il suffit bien d'avoir une solution approchée à 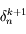 près.
près.
-
Question 7
Solution :
Il suffit d'inverser l'équation qui définie 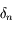 pour
pour 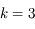 en l'écrivant sous la forme:
en l'écrivant sous la forme:
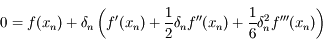 .
.
-
Question 8
Solution :
On a:
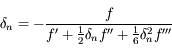
où on a omis la variable 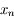 pour simplifier.
pour simplifier.
En utilisant le dévelopement limité de 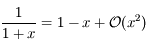 , on a:
, on a:
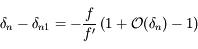 .
.
Or, d'après la définition de 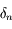 :
: 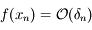 , donc
, donc 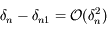 .
.
De même:
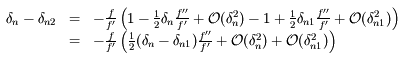 ,
,
qui, d'après le résultat précédent nous donne 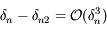 .
.
Enfin, on a:
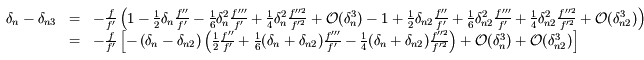 ,
,
En utilisant les résutlats précédents, on trouve bien: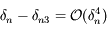 .
.
-
Question 9
Solution :
Inverser l'équation de Kepler, revient à résoudre 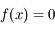 avec
avec 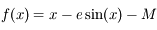 , avec l'excentricité
, avec l'excentricité 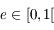 et l'anomalie moyenne
et l'anomalie moyenne ![M\in [0,2\pi]](../pages_dl/equations_dl/equation154.png) , des paramètres de l'équation.
, des paramètres de l'équation. 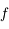 est évidement de classe
est évidement de classe 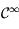 , et
, et 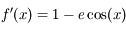 , ne s'annule effectivement jamais d'apèrs l'intervalle dans lequel
, ne s'annule effectivement jamais d'apèrs l'intervalle dans lequel 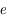 peut prendre ses valeurs.
L'application numérique est laissée au lecteur.
peut prendre ses valeurs.
L'application numérique est laissée au lecteur.

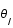 au lieu de
au lieu de 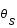 .
.

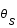 et
et 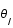 et de la distance OS.
et de la distance OS.
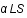 où l'angle de déviation,
où l'angle de déviation, 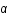 , vaut
, vaut 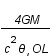 , avec G la constante de gravitation, M la masse de la lentille et c la vitesse de la lumière.
Dans l'approximation des petits angles, déterminer l'équation du second degré à laquelle obéit
, avec G la constante de gravitation, M la masse de la lentille et c la vitesse de la lumière.
Dans l'approximation des petits angles, déterminer l'équation du second degré à laquelle obéit 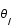 en fonction de
en fonction de 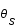 , et des grandeurs caractéristiques du système, LS, OS, OL et M.
, et des grandeurs caractéristiques du système, LS, OS, OL et M.
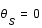 .
.
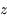 dépendant seulement de la variable
dépendant seulement de la variable 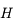 (angle horaire), démontrer que
(angle horaire), démontrer que 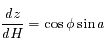 , puis
, puis 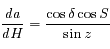 .
.
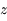 varie comme le carré de l'angle horaire (en se limitant au 2ème ordre).
varie comme le carré de l'angle horaire (en se limitant au 2ème ordre).

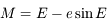 ,
,
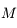 est l'anomalie moyenne,
est l'anomalie moyenne, 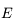 l'anomalie excentrique et
l'anomalie excentrique et 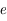 l'excentricité de la trajectoire.
l'excentricité de la trajectoire.
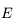 il est facile d'avoir
il est facile d'avoir 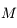 , mais en revanche connaissant
, mais en revanche connaissant 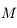 il n'est pas possible d'avoir
il n'est pas possible d'avoir 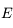 sous forme analytique. L'objet de cette exercice est justement de déterminer un algorithme puissant d'inversion de cette équation.
sous forme analytique. L'objet de cette exercice est justement de déterminer un algorithme puissant d'inversion de cette équation.
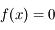 . Soit
. Soit 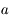 une solution à l'équation.
On supposera dans la suite que, sur un intervalle
une solution à l'équation.
On supposera dans la suite que, sur un intervalle 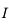 contenant
contenant 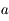 ,
, 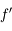 ne s'annulle jamais et que
ne s'annulle jamais et que 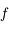 est de classe
est de classe 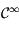 sur cet intervalle.
Soit
sur cet intervalle.
Soit 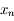 , la suite définie par :
, la suite définie par :
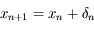 ,
,
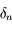 , la solution de
, la solution de 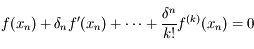 (
(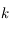 étant fixé).
étant fixé).
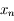 converge vers
converge vers 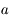 , alors elle converge au moins avec l'ordre
, alors elle converge au moins avec l'ordre 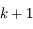 .
.
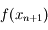 en fonction de
en fonction de 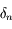 et un nombre
et un nombre 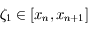 .
.
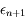 l'erreur de
l'erreur de 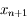 définie par
définie par 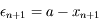 . Cacluler
. Cacluler 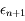 en fonction de
en fonction de 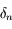 ,
, 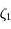 et un nombre
et un nombre 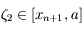 .
.
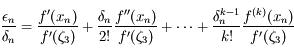 , avec
, avec 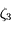 un nombre entre
un nombre entre 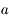 et
et 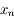 .
.
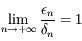 .
.
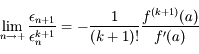 , et que la suite
, et que la suite 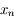 converge vers
converge vers 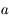 au moins à l'ordre
au moins à l'ordre 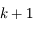 .
.
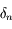 de l'équation qui le défini. Avant tout, jusitfier pourquoi il suffit d'avoir une solution approxée à
de l'équation qui le défini. Avant tout, jusitfier pourquoi il suffit d'avoir une solution approxée à 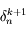 près.
près.
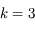 , on a:
, on a:
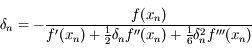
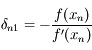 ,
,
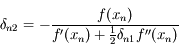 ,
,
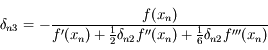 ,
,
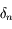 à
à 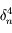 près. On pourra procéder par étape en montrant que
près. On pourra procéder par étape en montrant que 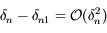 , puis que
, puis que 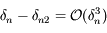 et enfin que
et enfin que 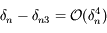 .
.
![[0,2\pi]](../pages_dl/equations_dl/equation149.png) . Aplliquer l'algorithme à quelque exemple et remarquer qu'on obtient une erreur inférieure à
. Aplliquer l'algorithme à quelque exemple et remarquer qu'on obtient une erreur inférieure à 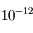 en moins de 4 itérations.
en moins de 4 itérations.
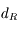 , en dessous de laquelle un satellite commence à se disloquer sous l'action des forces de marée causées par la planète autour de laquelle il orbite.
, en dessous de laquelle un satellite commence à se disloquer sous l'action des forces de marée causées par la planète autour de laquelle il orbite.
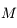 , rayon
, rayon 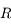 , et masse volumique
, et masse volumique 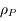 .
.
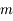 , de rayon
, de rayon 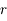 et de masse volumique
et de masse volumique 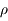 ), et qu'il est en orbite circulaire de rayon
), et qu'il est en orbite circulaire de rayon 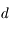 autour de la planète.
autour de la planète.

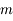 dans le repère lié à la planète (supposé galiléen) :
dans le repère lié à la planète (supposé galiléen) : 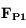 est la force d'attraction gravitationnelle de la planète,
est la force d'attraction gravitationnelle de la planète, 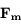 celle de la deuxième sphère de masse
celle de la deuxième sphère de masse 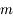 ,
, 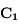 la force de contact entre les deux sphères.
la force de contact entre les deux sphères.
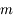 , montrer qu'au premier ordre en
, montrer qu'au premier ordre en 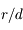 la vitesse
angulaire de la comète est
la vitesse
angulaire de la comète est 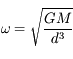 .
.
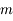 , et trouver un critère de fragmentation du satellite (contact rompu entre les deux sphères) au premier ordre en
, et trouver un critère de fragmentation du satellite (contact rompu entre les deux sphères) au premier ordre en 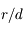 .
.
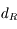 en fonction de
en fonction de 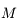 ,
, 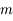 ,
, 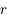 , puis en fonction de
, puis en fonction de 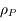 ,
, 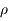 ,
, 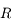 .
.
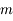 due à l'attraction gravitationnelle de la planète est supérieure à la force de gravitation mutuelle entre les deux sphères.
due à l'attraction gravitationnelle de la planète est supérieure à la force de gravitation mutuelle entre les deux sphères.
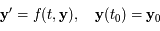 .
.
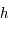 , un pas d'intégration. Le but est de trouver
, un pas d'intégration. Le but est de trouver 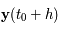 avec la meilleure précision possible.
avec la meilleure précision possible.
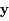 en
en 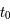 :
:
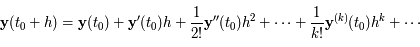
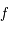 , une fonction analytique. On note
, une fonction analytique. On note 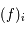 , le
, le 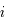 ème coefficient de Taylor de la fonction
ème coefficient de Taylor de la fonction 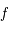 en
en 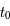 défini par :
défini par :
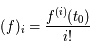 .
.
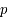 et
et 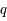 , deux fonctions analytiques, déterminer
, deux fonctions analytiques, déterminer 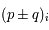 et
et 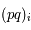
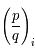 .
.
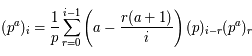
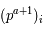
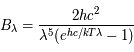
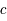 est la vitesse de la lumière dans le vide,
est la vitesse de la lumière dans le vide, 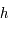 la constante de Planck,
la constante de Planck, 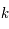 la constante de Boltzmann,
la constante de Boltzmann, 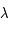 la longueur d'onde et
la longueur d'onde et 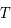 la température du corps noir.
la température du corps noir.
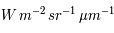 , du corps noir à toutes les longueurs d'onde.
, du corps noir à toutes les longueurs d'onde.


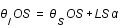
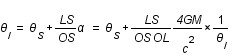
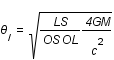
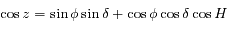
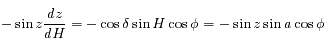 (formule des sinus).
(formule des sinus).
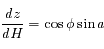 .
.
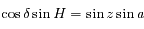 .
.
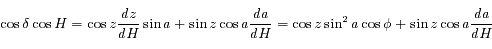 .
.
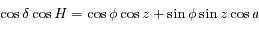 .
.
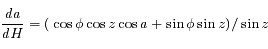 ,
et finalement
,
et finalement 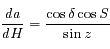 .
.
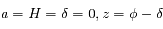 .
.
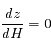 et
et 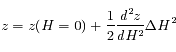 .
.
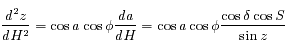 .
.
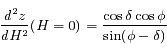 , et finalement:
, et finalement: 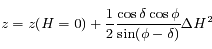 .
.
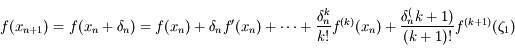 , avec
, avec 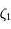 compris entre
compris entre 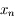 et
et 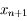 . D'après la définition de
. D'après la définition de 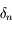 , on obtient:
, on obtient: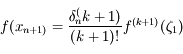 .
.
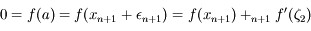 , avec
, avec 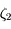 un nombre entre
un nombre entre 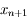 et
et 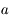 .
En combinant avec l'expression de
.
En combinant avec l'expression de 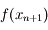 obtenue précédemment, et sachant que d'après nos hypothèses
obtenue précédemment, et sachant que d'après nos hypothèses 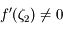 , on obtient:
, on obtient:
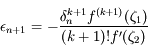 .
.
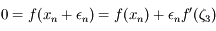 avec
avec 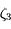 compris entre
compris entre 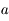 et
et 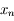 .
En remplaçant
.
En remplaçant 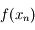 par
par 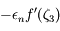 dans l'équation définissant
dans l'équation définissant 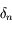 et en divisant par
et en divisant par 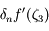 (ce que l'on peut faire puisque, d'après nos hypothèses,
(ce que l'on peut faire puisque, d'après nos hypothèses, 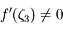 ) on obtient l'expression voulue.
) on obtient l'expression voulue.
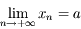 . Donc d'après la définition de
. Donc d'après la définition de 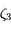 , on a aussi
, on a aussi 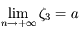 . Comme
. Comme 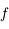 est de classe
est de classe 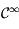 sur
sur 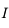 , sa dérivée première est continue, donc
, sa dérivée première est continue, donc 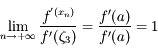 . Dautre part on a
. Dautre part on a 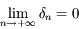 donc, d'après l'expression obtenue précedemment pour
donc, d'après l'expression obtenue précedemment pour 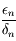 , on a bien la limite demandée.
, on a bien la limite demandée.
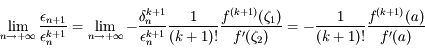 .
.
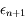 en fonction de
en fonction de 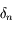 calculée prcédemment et la deuxième découle de la continuité des dérivées successives de
calculée prcédemment et la deuxième découle de la continuité des dérivées successives de 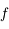 et de la définition de
et de la définition de 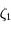 et
et 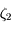 .
.
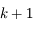 .
.
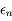 et
et 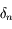 on a:
on a:
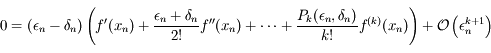 ,
,
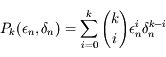 . Comme on a vu que
. Comme on a vu que 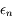 et
et 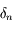 sont équivalents, on a bien:
sont équivalents, on a bien:
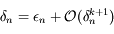 ,
,
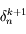 près.
près.
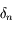 pour
pour 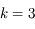 en l'écrivant sous la forme:
en l'écrivant sous la forme:
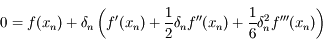 .
.
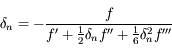
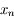 pour simplifier.
pour simplifier.
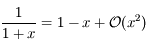 , on a:
, on a:
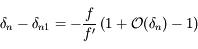 .
.
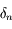 :
: 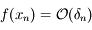 , donc
, donc 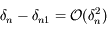 .
.
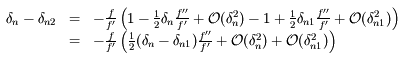 ,
,
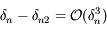 .
.
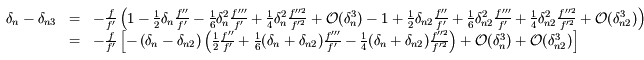 ,
,
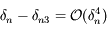 .
.
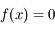 avec
avec 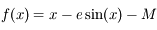 , avec l'
, avec l'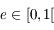 et l'
et l'![M\in [0,2\pi]](../pages_dl/equations_dl/equation154.png) , des paramètres de l'équation.
, des paramètres de l'équation. 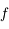 est évidement de classe
est évidement de classe 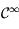 , et
, et 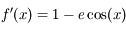 , ne s'annule effectivement jamais d'apèrs l'intervalle dans lequel
, ne s'annule effectivement jamais d'apèrs l'intervalle dans lequel 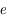 peut prendre ses valeurs.
L'application numérique est laissée au lecteur.
peut prendre ses valeurs.
L'application numérique est laissée au lecteur.
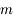 :
: 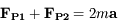 (les caractères en gras désignent des vecteurs)
(les caractères en gras désignent des vecteurs)
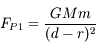 ,
, 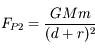
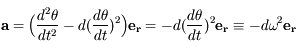 ,
,
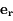 est un vecteur unitaire radial. On obtient alors :
est un vecteur unitaire radial. On obtient alors :
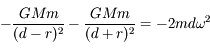
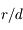 ,
, 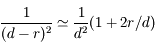 et
et 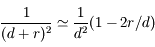
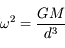 au premier ordre en
au premier ordre en 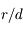 . On retrouve la troisième loi de Kepler.
. On retrouve la troisième loi de Kepler.
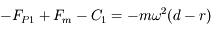 , avec
, avec 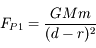 et
et 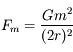 .
.
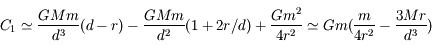
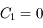 , i.e. lorsque
, i.e. lorsque 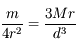 .
.
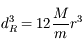
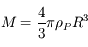 et
et 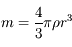 , on obtient :
, on obtient :
![d_R=R \sqrt[\displaystyle 3]{12 \frac{\rho_P}{\rho}} \simeq 2.29 R \sqrt[\displaystyle 3]{ \frac{\rho_P}{\rho}}](../pages_dl/equations_dl/equation205.png) .
.
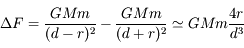 .
.
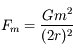
![\Delta F \geq F_m \Longleftrightarrow d \leq R \sqrt[\displaystyle 3]{16 \frac{\rho_P}{\rho}} \simeq 2.52 R \sqrt[\displaystyle 3]{\frac{\rho_P}{\rho}}](../pages_dl/equations_dl/equation209.png) .
.
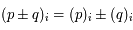
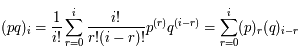
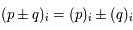
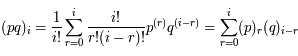
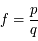 . Ainsi on a
. Ainsi on a 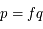 . D'après le résultat précédent on en déduit que
. D'après le résultat précédent on en déduit que 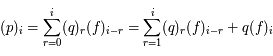 .
.
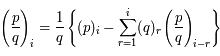
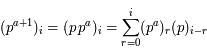 .
.
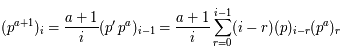
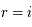 dans la première somme on trouve bien le résultat demandé.
dans la première somme on trouve bien le résultat demandé.