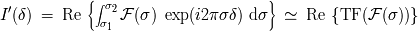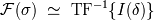Requisitos previos
Requisitos previos
Principio del interferómetro de Michelson, transformada de Fourier.
 Objetivos
Objetivos
Explicitar por qué se le dice
de Fourier a un interferómetro
Interferencias de 2 ondas
Se denota

y

respectivamente, a la diferencia y el desfase de camino entre 2 haces monocromáticos de luz
que interfieren en el infinito.

:
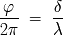
A partir de ahora se denotara, en función del numero de onda:
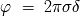
Como provienen de la misma fuente, los haces son coherentes. Sus amplitudes se sumarán.
Ello se escribe en notación compleja como:
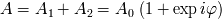
Interferograma
Dada una diferencia de camino de

entre los 2 espejos, la intensidad difractada sobre el eje (es decir dentro del anillo central)
constituye el
interferograma. En luz monocromática de numero de onda

, la señal de interferencia, para una diferencia de camino

, se escribe:
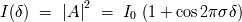
Las unidades empleadas típicamente son los números de onda en
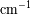
y la diferencia de camino en cm. El periodo espacial del interferograma es
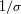
, es decir simplemente el tamaño de onda

.
Interferencias y transformada de Fourier
Imaginamos una fuente de luz no monocromática, con una densidad espectral
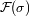
, en la banda espectral
![[s1,s2]](../../../../images/fourier/images-TeX4ht/fourier17x.png)
. Su interferograma vale:
![integral s2 I (d) = F (s) [1 + cos 2psd] ds s1](../../../../images/fourier/images-TeX4ht/fourier18x.png)
Sin
coherencia temporal
entre los colores, se suma las intensidades espectrales:
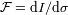
.
La parte
modulada del interferograma (es decir la que depende de la diferencia de camino

) corresponde a la parte real de la Transformada de Fourier (TF a partir de ahora) de la densidad
espectral:
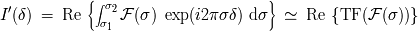
En realidad, el interferograma realiza la TF de la distribución espectral de la fuente de luz. Asi, el
espectro se consigue tomando la TF inversa del interferograma:
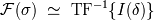
Como esta ultima etapa consiste únicamente en un calculo, se requiere potencia de computación.
Así, el desarrollo de los espectros de transformada de Fourier fue paralelo al de los
ordenadores.

 y
y
 respectivamente, a la diferencia y el desfase de camino entre 2 haces monocromáticos de luz
que interfieren en el infinito.
respectivamente, a la diferencia y el desfase de camino entre 2 haces monocromáticos de luz
que interfieren en el infinito.
 :
:
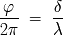
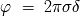
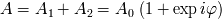
 entre los 2 espejos, la intensidad difractada sobre el eje (es decir dentro del anillo central)
constituye el interferograma. En luz monocromática de numero de onda
entre los 2 espejos, la intensidad difractada sobre el eje (es decir dentro del anillo central)
constituye el interferograma. En luz monocromática de numero de onda
 , la señal de interferencia, para una diferencia de camino
, la señal de interferencia, para una diferencia de camino
 , se escribe:
, se escribe:
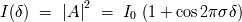
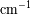 y la diferencia de camino en cm. El periodo espacial del interferograma es
y la diferencia de camino en cm. El periodo espacial del interferograma es
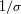 , es decir simplemente el tamaño de onda
, es decir simplemente el tamaño de onda
 .
.
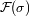 , en la banda espectral
, en la banda espectral
![[s1,s2]](../../../../images/fourier/images-TeX4ht/fourier17x.png) . Su interferograma vale:
. Su interferograma vale:
![integral s2 I (d) = F (s) [1 + cos 2psd] ds s1](../../../../images/fourier/images-TeX4ht/fourier18x.png)
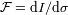 .
La parte modulada del interferograma (es decir la que depende de la diferencia de camino
.
La parte modulada del interferograma (es decir la que depende de la diferencia de camino
 ) corresponde a la parte real de la Transformada de Fourier (TF a partir de ahora) de la densidad
espectral:
) corresponde a la parte real de la Transformada de Fourier (TF a partir de ahora) de la densidad
espectral: