 Objetivos
Objetivos
La estadística de Poisson está adaptada a un fenómeno regular cuantificado.
La detección de una radiación electromagnética es un ejemplo concreto de esta estadística: ya que la llegada de
la energía está
cuantificada en fotones.
Cuanto mayor sea la cantidad de fotones esperada mejor podremos precisar el valor promedio observado.
Un ejemplo concreto... y discreto
Abordamos la estadística de Poisson con un caso concreto: el análisis de la llegada de fotones
de una señal luminosa de promedio constante.
Una radiación monocromática de frecuencia

, de luminosidad
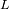
observada durante un tiempo
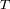
aporta una energía

. Esta radiación es llevada por una
cantidad promedio de fotones
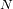
que obedece a:
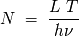
La
discretización del flujo en cuentas de energía implica que la cantidad de fotones que
llega por intervalo de tiempo fluctúa alrededor de este promedio.
Llegada de los fotones
La probabilidad de detectar

fotones cuando se esperan
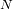
(en promedio) se escribe:
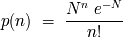
Es la ley de Poisson de promedio
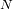
. Hay que acordarse que
-
la probabilidad máxima se consegue para
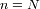 .
.
-
La desviación estándar de la distribución vale
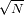 .
.
 Demostración
Demostración
Cortamos el intervalo de tiempo en

partes lo bastante pequeñas como para asegurar que sólo
un fotón llega durante el
intervalo
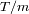
. Podemos estimar la probabilidad de ver llegar

fotones guardándolos en

cajas.
La probabilidad de tener un fotón por caja temporal es
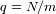
y la probabilidad opuesta

. Como hay
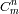
maneras de guardar

fotones en

cajas, conseguimos finalmente:
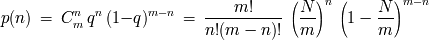
Con un numero

muy grande de intervalos, volvemos a encontrar la ley enunciada:
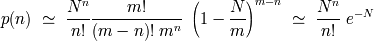
Dadas la aproximaciones para
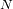
grande y
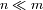
:
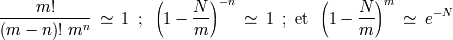
Extrapolación a valores grandes
Para grandes valores de
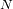
,
podemos demostrar
que esta ley se confunde con la de Gauss:
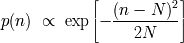
Concluímos entonces, basándonos en la
estadística gaussiana
que para un valor promedio
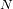
, la desviación estándar vale
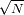
.
A partir de ello se deduce algo importante: cuando
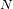
crece, la desviación estándar crece, pero la razón desviación estándar/promedio disminuye.

 , de luminosidad
, de luminosidad
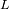 observada durante un tiempo
observada durante un tiempo
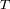 aporta una energía
aporta una energía
 . Esta radiación es llevada por una cantidad promedio de fotones
. Esta radiación es llevada por una cantidad promedio de fotones
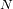 que obedece a:
que obedece a:
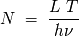
 fotones cuando se esperan
fotones cuando se esperan
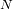 (en promedio) se escribe:
(en promedio) se escribe:
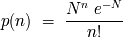
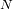 . Hay que acordarse que
. Hay que acordarse que
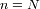 .
.
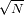 .
. partes lo bastante pequeñas como para asegurar que sólo un fotón llega durante el
intervalo
partes lo bastante pequeñas como para asegurar que sólo un fotón llega durante el
intervalo
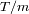 . Podemos estimar la probabilidad de ver llegar
. Podemos estimar la probabilidad de ver llegar
 fotones guardándolos en
fotones guardándolos en
 cajas.
cajas.
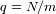 y la probabilidad opuesta
y la probabilidad opuesta
 . Como hay
. Como hay
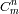 maneras de guardar
maneras de guardar
 fotones en
fotones en
 cajas, conseguimos finalmente:
cajas, conseguimos finalmente:
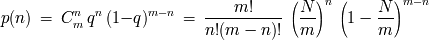
 muy grande de intervalos, volvemos a encontrar la ley enunciada:
muy grande de intervalos, volvemos a encontrar la ley enunciada:
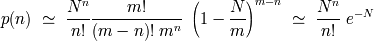
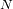 grande y
grande y
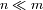 :
:
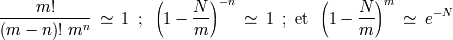
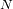 , podemos demostrar
que esta ley se confunde con la de Gauss:
, podemos demostrar
que esta ley se confunde con la de Gauss:
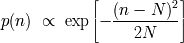
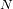 , la desviación estándar vale
, la desviación estándar vale
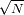 .
.
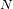 crece, la desviación estándar crece, pero la razón desviación estándar/promedio disminuye.
crece, la desviación estándar crece, pero la razón desviación estándar/promedio disminuye.