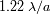Requisitos previos
Requisitos previos
Difracción de Fraunhofer.
 Objetivos
Objetivos
Mostrar la relación entre la difracción y la resolución última de un sistema óptico.
Resolución limite
La resolución limite depende del tamaño de la pupila y de la longitud de onda. Mejorar este
limite motiva la construcción de colectores con espejos más grandes, sobre todo a grandes
longitudes de onda.
La
tabla adjunta
presenta varias manchas imagen. Para hacerse una idea de los tamaños angulares en cuestión, la tabla
también presenta la distancia a la cual se ve una manzana con el diámetro angular
correspondiente.
Mancha imagen
| Instrumento |

|
|

|
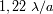
|
manzana |
| |
|
|
|
" |
(distancia en km) |
| ojo |
7 |
mm |
vis. |
18 |
1.1 |
| pequeño telescopio |
12 |
cm |
vis. |
1 |
20 |
| ISO, espacial |
60 |
cm |
IR |
8 |
2.6 |
| VLT, Chile |
8 |
m |
vis. |
0.015 |
1400 |
| VLT, Chile |
8 |
m |
20  m
m |
0.6 |
33 |
| antena VLBI |
70 |
m |
21 cm |
12' |
27 m |
| red VLBI |
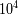
|
km |
21 cm |
0.005 |
4000 |
Resolución limite inducida por la difracción. Para ayudar el entendimiento de
los ordenes de magnitud, se indica la distancia a la cual se ve una manzana (de
diámetro 10 cm) con un diámetro angular similar.
Criterio de Rayleigh
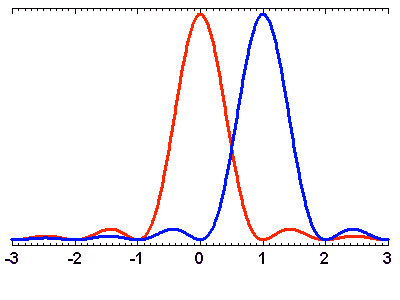
Ilustración del criterio de Rayleigh. La abscisa se expresa directamente en unidades de
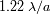
Crédito : Astrophysique sur Mesure
Criterio de Rayleigh
El criterio de Rayleigh precisa en que condiciones se pueden distinguir dos fuentes puntuales.
El primer cero de la difracción de una tiene que corresponder al máximo de la otra.



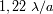
 m
m