 Objetivos
Objetivos
El caso de una fuente rigurosamente puntual y monocromática es evocado muy a menudo para explicar
conceptos ópticos. Pero una fuente real en astrofísica no tiene por qué ser puntual.
La coherencia espacial describe la extensión angular de la fuente. Un análisis detallado de los fenómenos se
puede escribir con un formalismo matemático y se apoya en el teorema de Zernike Van-Cittert.
Coherencia espacial
Las fuentes astrofísicas no son coherentes naturalmente. Su extensión angular conduce a la
degradación de la coherencia de la radiación: la onda colectada mezcla diversas direcciones
incidentes con varias fases. Su mezcla degrada la coherencia.
Para modelizar este fenómeno nos interesamos en la coherencia del campo sobre una pantalla
iluminada por una fuente lejana. Esta pantalla ilustra el papel de un plano de onda intermedio
o de una pupila.
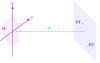
El factor de coherencia
Localizamos un punto
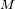
de la fuente por el rayo vector
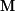
de coordenadas

e

. Comparamos la coherencia entre 2 puntos
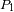
y
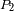
de la pantalla.
Para una fuente a gran distancia (

muy grande con respecto a las otras dimensiones), definimos el grado de coherencia como una
función del perfil de luminosidad
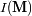
:
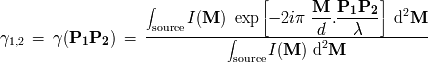
El factor de coherencia complejo corresponde a la transformada de Fourier de la distribución
espacial de intensidad de la fuente (teorema de Zernike - Van Cittert).
Caso particular : fuente circular
Modelizamos la radiación estelar por una fuente circular de diámetro
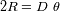
de luminosidad uniforme. Esta fuente es observada a una distancia
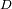
. Entonces, la luminosidad puede ser representada por una función rectángulo
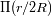
. Tratamos este caso con la ayuda de la geometría cilíndrica. Reescribimos la coherencia entre el
centro
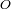
de la pantalla y un punto
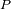
como
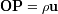
:
![integral ( Du ) [ r ] TT ----- exp - 2ip u. -- du source 2R c g1,2 = ----------- integral --------(------)------------------ Du--- source TT du 2R ( ) r- integral h [ r ] 2J1 2ph oc exp - 2ip u. -- du = ------------c--- 0 c r- 2ph c 2J1(X ) r = ---------- avec X = 2ph -- X c](../../../../images/optica/images-TeX4ht/optica459x.png)
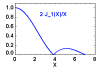
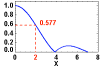
encontramos otra vez la
función de Bessel
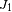
.
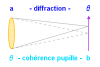
Recuerdos sobre la difracción de Fraunhofer
El resultado precedente se parece mucho al de la difracción. ¿ Es una
casualidad
?
La mancha de Airy que resulta de la difracción por una pupila circular tiene en cuenta la contribución
de todas la fuentes secundarias que hay que considerar sobre la pupila. Cuanto más grande es la
pupila más se acumulan los desfases (cuando nos alejamos del centro de la imagen
geométrica). Entonces la mancha de difracción es más fina cuanto más grande es la
pupila.
Hablando de coherencia, cuanto más grande es la pupila más disminuye el grado de coherencia entre dos
puntos de la misma.
Otra manera de formular esto deriva del análisis de Fourier: cuanto más información tenemos sobre una
señal y menos localizada se encuentra ésta. Es una ilustración directa del principio de incertidumbre de
Heisenberg.
Extensión de coherencia
La fuente de radio angular

es vista desde la pantalla con un ángulo solido
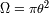
. Una superficie
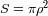
de la pantalla corresponde a una
extensión de haz
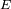
de:
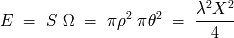
El valor a media altura del factor de coherencia corresponde a

: elegimos este valor para definir el radio de la extensión de coherencia.
 Definición
Definición
La extensión de coherencia del haz monocromático vale
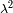
.

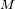 de la fuente por el rayo vector
de la fuente por el rayo vector
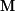 de coordenadas
de coordenadas
 e
e
 . Comparamos la coherencia entre 2 puntos
. Comparamos la coherencia entre 2 puntos
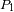 y
y
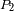 de la pantalla.
Para una fuente a gran distancia (
de la pantalla.
Para una fuente a gran distancia (
 muy grande con respecto a las otras dimensiones), definimos el grado de coherencia como una
función del perfil de luminosidad
muy grande con respecto a las otras dimensiones), definimos el grado de coherencia como una
función del perfil de luminosidad
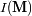 :
:
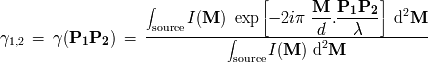
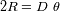 de luminosidad uniforme. Esta fuente es observada a una distancia
de luminosidad uniforme. Esta fuente es observada a una distancia
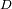 . Entonces, la luminosidad puede ser representada por una función rectángulo
. Entonces, la luminosidad puede ser representada por una función rectángulo
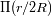 . Tratamos este caso con la ayuda de la geometría cilíndrica. Reescribimos la coherencia entre el
centro
. Tratamos este caso con la ayuda de la geometría cilíndrica. Reescribimos la coherencia entre el
centro
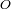 de la pantalla y un punto
de la pantalla y un punto
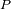 como
como
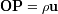 :
: ![integral ( Du ) [ r ] TT ----- exp - 2ip u. -- du source 2R c g1,2 = ----------- integral --------(------)------------------ Du--- source TT du 2R ( ) r- integral h [ r ] 2J1 2ph oc exp - 2ip u. -- du = ------------c--- 0 c r- 2ph c 2J1(X ) r = ---------- avec X = 2ph -- X c](../../../../images/optica/images-TeX4ht/optica459x.png)
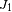 .
.
 es vista desde la pantalla con un ángulo solido
es vista desde la pantalla con un ángulo solido
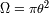 . Una superficie
. Una superficie
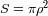 de la pantalla corresponde a una extensión de haz
de la pantalla corresponde a una extensión de haz
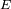 de:
de:
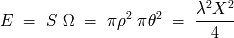
 : elegimos este valor para definir el radio de la extensión de coherencia.
: elegimos este valor para definir el radio de la extensión de coherencia.
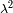 .
.