 Objetivos
Objetivos
Muchas fuentes astrofísicas presentan un diámetro angular que no se puede resolver con una pupila única.
Pero la interferometría permite mejorar la resolución espacial y
medir diámetros estelares.
Fuente puntual extensa
El diámetro de una estrella cercana al Sol cubre un ángulo del orden de un milisegundo de arco. Este
diámetro es mucho más pequeño que la mancha de difracción de un telescopio en el visible (incluso para
un telescopio de gran diámetro). Pero, podemos medir este diámetro de manera indirecta gracias a la
interferometría,
si disponemos de una base lo suficiente extensa.
Suponemos una fuente uniforme, circular de diámetro angular

, observada con 2 telescopios idénticos separados por una base

(base proyectada en un plano perpendicular a la fuente). La luz de los dos telescopios
interfiere.
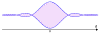
Visibilidad y medida de un diámetro estelar
El
factor de coherencia
establecido en el caso general es llamado
visibilidad de manera usual. La función de visibilidad se
escribe:
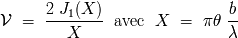
donde
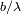
es la frecuencia espacial.
Cada base

conduce a una medida de la
visibilidad
para la frecuencia espacial
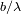
. La visibilidad se anula para
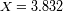
. Como la estrella es modelizada como un disco uniforme, ello corresponde a una relación entre el
diámetro angular estelar y la frecuencia espacial:
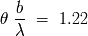
Vemos que para medir el diámetro estelar

sólo se necesita medir la
visibilidad de la figura de interferencia.
El calculo precedente suponía que la fuente tiene un perfil uniforme: en realidad, el fenómeno de
oscurecimiento centro-borde complica un poco el análisis. El papel de la difracción tampoco
puede ser olvidado: cada medida de visibilidad tiene que ser corregida de la función de
aparato de los colectores (incluyendo la difracción), que puede ser determinada de manera
experimental sobre una fuente
realmente puntual (en la práctica se utiliza una estrella muy
lejana).

Resolución angular
Una pupila única es un
filtro pasa baja: corta las frecuencias espaciales a
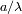
(y tiene por ello una resolución angular de
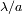
.
Un interferómetro es un
filtro pasa banda: procura una información a la frecuencia
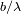
con una resolución espacial
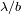
.
Encontramos estas propiedades con un análisis de Fourier: el teorema de Wiener-Khintchine
relaciona la función de transito óptico con la transformada de Fourier inversa de la
autocorrelación
de la pupila.
Síntesis de apertura
Una medida del factor de coherencia complejo proporciona un componente de la frecuencia
espacial de la fuente. La medida de este factor a varias frecuencias espaciales permite reconstruir
la distribución espacial de intensidad de la fuente.

 , observada con 2 telescopios idénticos separados por una base
, observada con 2 telescopios idénticos separados por una base
 (base proyectada en un plano perpendicular a la fuente). La luz de los dos telescopios
interfiere.
(base proyectada en un plano perpendicular a la fuente). La luz de los dos telescopios
interfiere.
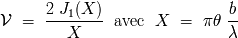
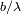 es la frecuencia espacial.
es la frecuencia espacial.
 conduce a una medida de la visibilidad
para la frecuencia espacial
conduce a una medida de la visibilidad
para la frecuencia espacial
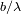 . La visibilidad se anula para
. La visibilidad se anula para
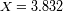 . Como la estrella es modelizada como un disco uniforme, ello corresponde a una relación entre el
diámetro angular estelar y la frecuencia espacial:
. Como la estrella es modelizada como un disco uniforme, ello corresponde a una relación entre el
diámetro angular estelar y la frecuencia espacial:
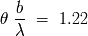
 sólo se necesita medir la visibilidad de la figura de interferencia.
sólo se necesita medir la visibilidad de la figura de interferencia.
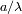 (y tiene por ello una resolución angular de
(y tiene por ello una resolución angular de
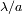 .
.
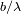 con una resolución espacial
con una resolución espacial
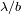 .
.