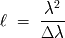Objetivos
Objetivos
El caso de una fuente rigurosamente puntual y monocromática se evoca a menudo para explicar la óptica
geométrica y física. Pero una fuente nunca es totalmente monocromática. Incluso cuando presenta líneas de
emisión muy estrechas o si sólo es seleccionado (con filtros) un intervalo espectral muy fino. La coherencia
temporal de una onda tiene en cuenta sus colores.
Para ser rigurosos, precisamos del teorema de Wiener-Khintchine.
 Requisitos previos
Requisitos previos
Interferómetro de Michelson.
Coherencia temporal
Cualquier fenómeno de interferencia con una fuente monocromática conduce a una modulación
de la amplitud resultante en función de la longitud de onda.
Para una fuente policromática, mezclar los colores consiste en mezclar periodos diferentes: la
coherencia temporal de la señal da problemas.
Ejemplo : interferometría por transformada de Fourier
(Consultar las
paginas dedicadas al espectrómetro de transformada de Fourier
)
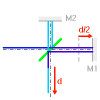
El ejemplo de un
interferómetro por transformada de Fourier
(en forma de anillo) muestra la problemática: la visibilidad de las franjas disminuye más rápidamente
cuanto más grande sea el intervalo espectral.
Para una línea monocromática, el interferograma se escribe (en función de la diferencia de
camino):
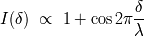
Para una línea
real de un tamaño dado (y no infinitamente fina), hay que tener en cuenta la
contribución de las varias componentes espectrales.
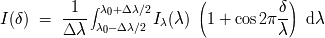
La integración (función del perfil
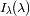
de la línea), conduce a :
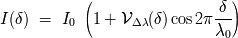

La función de
visibilidad de las franjas
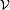
:
- tiene una extensión proporcional a
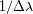
- disminuye con la diferencia de camino

Un ejemplo de demostración (en un caso simplificado) viene dado en este
ejercicio.
Definición de la coherencia temporal
En el caso general, el grado de coherencia de una fuente policromática, compleja, se escribe:
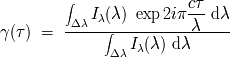
La demostración se apoya en el teorema de Wiener-Khintchine.
El tamaño de coherencia
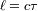
que mide la extensión del grado de coherencia verifica aproximadamente:
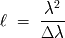

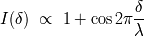
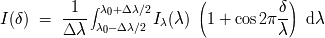
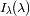 de la línea), conduce a :
de la línea), conduce a :
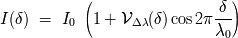
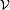 :
:
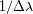

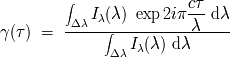
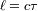 que mide la extensión del grado de coherencia verifica aproximadamente:
que mide la extensión del grado de coherencia verifica aproximadamente: