 Objetivos
Objetivos
Ilustrar el problema de N cuerpos en un caso particular: tres cuerpos, de los cuales uno tiene masa despreciable
con respecto a los otros dos. En ese caso sólo se considera el campo gravitacional de los dos cuerpos masivos.
Tres cuerpos, pero uno de masa nula
El problema de tres cuerpos es irresoluble por lo general. El astrónomo y matemático
Joseph-Louis Lagrange propuso una solución en un caso particular, donde uno de los cuerpos
era de masa despreciable con respecto a los otros dos, y sufre sus campos gravitacionales.
El potencial gravitacional
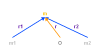
Se supone que los dos cuerpos masivos están en una órbita circular; se denota como

a la velocidad angular de rotación. El potencial gravitacional creado por estos dos cuerpos es estudiado
en el referencial giratorio con los dos cuerpos. Las notaciones están definidas en la
figura
adjunta.
El cuerpo de masa despreciable sufre un potencial:
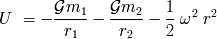
donde
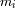
son las masas respectivas de los dos cuerpos masivos,

las distancias del sistema de dos cuerpos,

la distancia a su baricentro y

la velocidad angular de rotación de los dos cuerpos. El último término es debido al referencial
giratorio.
Introduciendo

como la razón de las masas
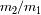
, y denotando
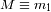
a la masa superior, se obtiene:
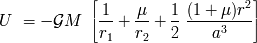
habiendo introducido la
tercera ley de Kepler
para los dos cuerpos masivos:
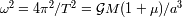
.
Los puntos de Lagrange
El gradiente de potencial se anula en unos
puntos particulares
: los puntos de Lagrange. Su estudio se puede hacer analíticamente, pero aquí nos contentaremos con
constatar los resultados.
Estos puntos se sitúan en el plano orbital de los dos cuerpos. Los puntos L1, L2 y L3 están alineados
con los dos cuerpos, y L4 y L5 forman con ellos dos triángulos equiláteros.
Equilibrio en los puntos de Lagrange
Hay que destacar que las posiciones de equilibrio encontradas no son estables estáticamente:
corresponden en efecto a máximos de potencial, o puntos de silla. Es dinámicamente, con
el apoyo de la fuerza de Coriolis (el referencial es giratorio) cuando los puntos L4 y L5 se
convierten en estables... y de hecho son ocupados por satélites naturales o artificiales.

 a la velocidad angular de rotación. El potencial gravitacional creado por estos dos cuerpos es estudiado
en el referencial giratorio con los dos cuerpos. Las notaciones están definidas en la figura
adjunta.
a la velocidad angular de rotación. El potencial gravitacional creado por estos dos cuerpos es estudiado
en el referencial giratorio con los dos cuerpos. Las notaciones están definidas en la figura
adjunta.
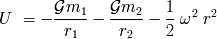
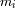 son las masas respectivas de los dos cuerpos masivos,
son las masas respectivas de los dos cuerpos masivos,
 las distancias del sistema de dos cuerpos,
las distancias del sistema de dos cuerpos,
 la distancia a su baricentro y
la distancia a su baricentro y
 la velocidad angular de rotación de los dos cuerpos. El último término es debido al referencial
giratorio.
la velocidad angular de rotación de los dos cuerpos. El último término es debido al referencial
giratorio.
 como la razón de las masas
como la razón de las masas
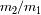 , y denotando
, y denotando
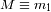 a la masa superior, se obtiene:
a la masa superior, se obtiene:
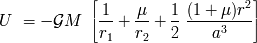
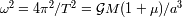 .
.