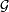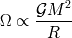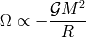Objetivos
Objetivos
Medir la energía de la acreción de un cuerpo denso.
Análisis dimensional
Nos vamos a interesar al caso de un cuerpo autogravitante de masa
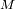
y radio
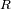
. ¿Qué energía proveniente de su gravitación se le asocia?
La análisis dimensional nos permite tener una primera respuesta. A partir de las características
del objeto y de la constante gravitacional
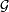
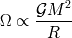
Para convencerse, basta volver a la definición de la
interacción gravitacional.
Energía potential de interacción gravitacional
Con un poco de física, podemos obtener información suplementaria:
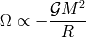
La interacción siendo atractiva, necesariamente la energía asociada a un cuerpo denso es
negativa : en efecto, para destruir el objeto sería necesario ejercer un trabajo positivo para
dispersar muy lejos sus partículas.
Cuanto más masivo y/o condensado sea el objeto más negativa será su energía potencial de
interacción gravitacional.
Ver el
ejercicio
para un cálculo completo de la energía potencial.

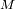 y radio
y radio
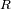 . ¿Qué energía proveniente de su gravitación se le asocia?
. ¿Qué energía proveniente de su gravitación se le asocia?