En la sección
brillo espectral
del cuerpo negro se expresa en función de la frecuencia de la forma siguiente :
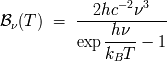
En este ejercicio, se propone mostrar cómo los radio-astronomos expresan la luminosidad radio como
una temperatura en Kelvin.
Las leyes de la
difracción
enuncian que un haz luminoso elemental observado a una extensión
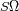
es igual a
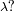
y que la medida sólo puede dar acceso a una dirección de polarización. La integración
en
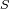
y
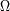
permite convertir el brillo espectral en una potencia espectral.
La superficie
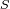
representa aquí la superficie colectora y
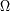
el ángulo solido bajo el cual se ve la fuente elemental.
1)
Demostrar que, en el dominio de las radiofrecuencias, la frecuencia de observación

del orden del unos cuantos GHz, verifica para las temperaturas encontradas en el Universo
:
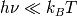
Se da
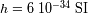
, y
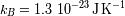
. Se considera una nube molecular a 10K y una radiación a longitudes de onda superiores a
1cm.
ayuda
solución

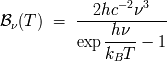
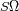 es igual a
es igual a
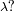 y que la medida sólo puede dar acceso a una dirección de polarización. La integración
en
y que la medida sólo puede dar acceso a una dirección de polarización. La integración
en
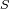 y
y
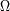 permite convertir el brillo espectral en una potencia espectral.
permite convertir el brillo espectral en una potencia espectral.
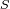 representa aquí la superficie colectora y
representa aquí la superficie colectora y
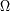 el ángulo solido bajo el cual se ve la fuente elemental.
el ángulo solido bajo el cual se ve la fuente elemental.
 del orden del unos cuantos GHz, verifica para las temperaturas encontradas en el Universo
:
del orden del unos cuantos GHz, verifica para las temperaturas encontradas en el Universo
:
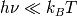
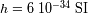 , y
, y
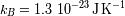 . Se considera una nube molecular a 10K y una radiación a longitudes de onda superiores a
1cm.
ayuda
solución
. Se considera una nube molecular a 10K y una radiación a longitudes de onda superiores a
1cm.
ayuda
solución
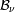 en función de las variables angulares y de superficie conducen a una densidad espectral de
potencia
igual a
en función de las variables angulares y de superficie conducen a una densidad espectral de
potencia
igual a
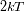 ayuda
ayuda
solución
ayuda
ayuda
solución