Potencia total radiada
 Objetivos
Objetivos
Establecer un balance de la potencia emitida por un cuerpo negro estelar.
‘? Qué potencia radia una estrella a una temperatura de equilibro
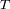
, asimilable a un cuerpo negro de temperatura
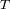
, con una geometria esférica de radio
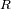
? Para responder a esta pregunta es necesario integrar el brillo espectral del cuerpo
negro sobre toda su superficie, en todas las direcciones y a todas las longitudes de
onda.
El cálculo proporciona una ley de potencia :
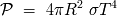
siendo la constante de Stefan :
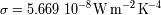
.
Potencia total radiada
La presencia de los términos
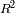
y
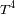
en la ecuación de la potencia total radiada se puede justificar rapidamente. En efecto, la
integración espacial, angular y espectral del brillo espectral:
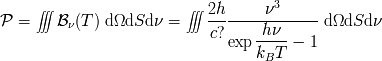
implica, la dependencia en función del radio, un término proporcional a la superficie estelar,
que varía según
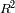
, y para el término de temperatura, un término propocional a
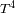
, puesto en evidencia por el cambio de variable
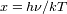
, que conduce a :
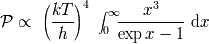
Los términos no explícitos en esta ecuación no dependen de la temperatura, ni de la integral de la
variable

, sino que tienen como valor un simple número
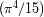
.
La ley en
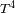
implica una gran diversidad en la vida de las estrellas. Dos estrellas con radios análogos pero con una
temperatura que varíe de una potencia simple al quíntuple (4000-20000K p.ex.) tendrán luminosidads
muy diferentes, con una razón de 625. La diferencia de temperatura entre las dos estrellas tendrá una
influencia muy fuerte sobre la
evolución
de ambas estrellas.

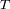 , asimilable a un cuerpo negro de temperatura
, asimilable a un cuerpo negro de temperatura
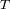 , con una geometria esférica de radio
, con una geometria esférica de radio
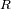 ? Para responder a esta pregunta es necesario integrar el brillo espectral del cuerpo
negro sobre toda su superficie, en todas las direcciones y a todas las longitudes de
onda.
? Para responder a esta pregunta es necesario integrar el brillo espectral del cuerpo
negro sobre toda su superficie, en todas las direcciones y a todas las longitudes de
onda.
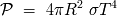
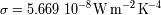 .
.
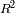 y
y
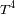 en la ecuación de la potencia total radiada se puede justificar rapidamente. En efecto, la
integración espacial, angular y espectral del brillo espectral:
en la ecuación de la potencia total radiada se puede justificar rapidamente. En efecto, la
integración espacial, angular y espectral del brillo espectral:
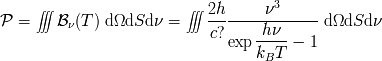
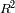 , y para el término de temperatura, un término propocional a
, y para el término de temperatura, un término propocional a
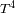 , puesto en evidencia por el cambio de variable
, puesto en evidencia por el cambio de variable
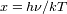 , que conduce a :
, que conduce a :
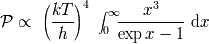
 , sino que tienen como valor un simple número
, sino que tienen como valor un simple número
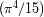 .
.
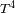 implica una gran diversidad en la vida de las estrellas. Dos estrellas con radios análogos pero con una
temperatura que varíe de una potencia simple al quíntuple (4000-20000K p.ex.) tendrán luminosidads
muy diferentes, con una razón de 625. La diferencia de temperatura entre las dos estrellas tendrá una
influencia muy fuerte sobre la evolución
de ambas estrellas.
implica una gran diversidad en la vida de las estrellas. Dos estrellas con radios análogos pero con una
temperatura que varíe de una potencia simple al quíntuple (4000-20000K p.ex.) tendrán luminosidads
muy diferentes, con una razón de 625. La diferencia de temperatura entre las dos estrellas tendrá una
influencia muy fuerte sobre la evolución
de ambas estrellas.