Statistique de Poisson
Lorsqu'une moyenne de 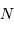 quanta par unité de temps est attendue, un détecteur idéal (rendement unité) en comptera un nombre plus ou moins voisin de
quanta par unité de temps est attendue, un détecteur idéal (rendement unité) en comptera un nombre plus ou moins voisin de 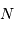 . La distribution des valeurs dépend du nombre N :
10,
100,
1000.
Plus
. La distribution des valeurs dépend du nombre N :
10,
100,
1000.
Plus 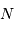 est grand, plus la distribution apparaît piquée en valeur relative, quand bien même elle est plus étalée en valeur absolue.
est grand, plus la distribution apparaît piquée en valeur relative, quand bien même elle est plus étalée en valeur absolue.
Distribution de Poisson
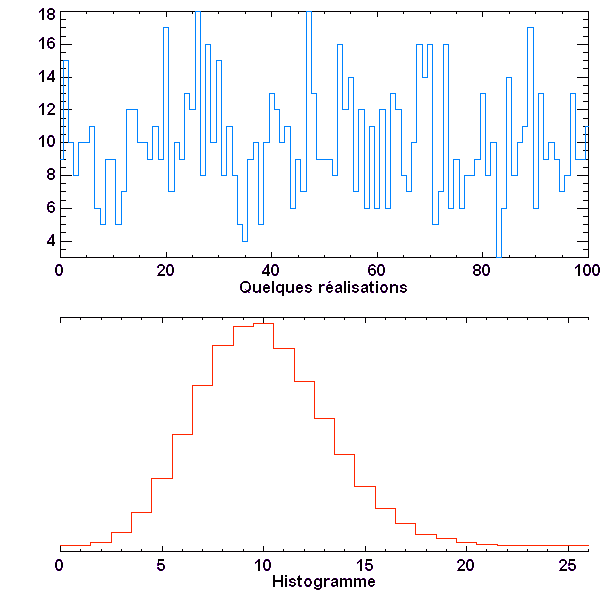
Série de valeurs et histogramme, dans le cas N = 10
Crédit :
ASM
Distribution de Poisson
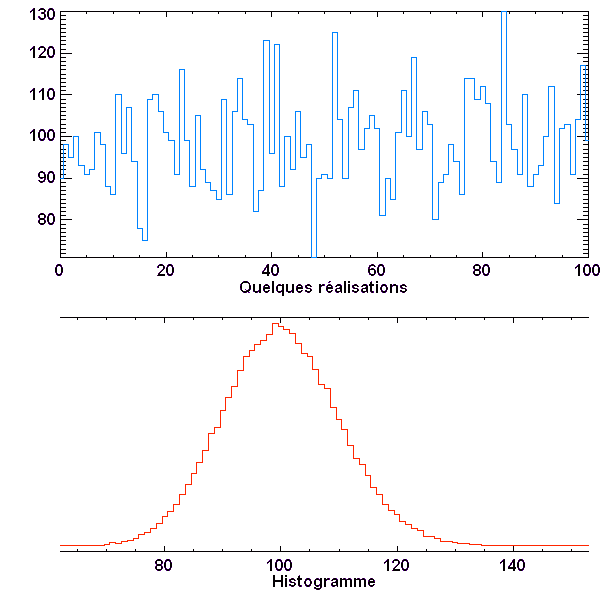
Série de valeurs et histogramme, dans le cas N = 100
Crédit :
ASM
Distribution de Poisson
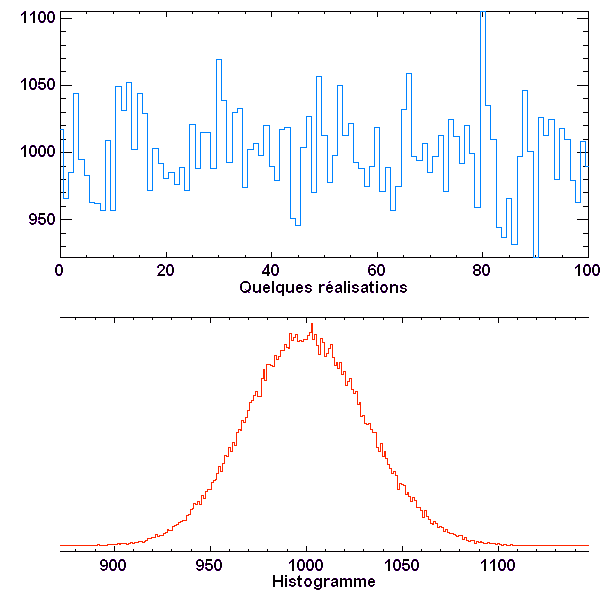
Série de valeurs et histogramme, dans le cas N = 1000
Crédit :
ASM
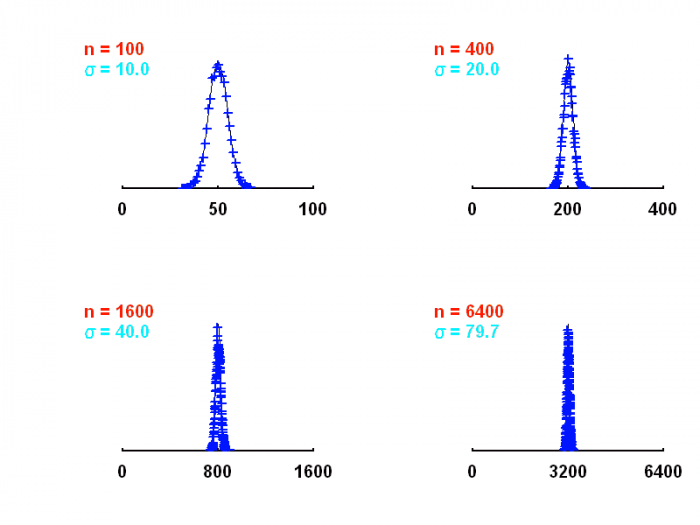
Statistiques poissonniennes. La dispersion relative décroît avec le nombre de quanta attendus.
Crédit :
ASM
 Objectifs
Objectifs
La statistique de Poisson concerne un phénomène régulier quantifié.
La détection d'un rayonnement électromagnétique en est un exemple concret, l'arrivée d'énergie étant quantifiée en photons.
Plus le nombre de photons attendus est grand, mieux on pourra préciser la valeur moyenne observée.
Un exemple concret... et discret
La statistique de Poisson va être abordée via un cas concret. L'analyse de l'arrivée de photons d'une signal lumineux de moyenne constante.
Un rayonnement monochromatique de fréquence 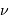 de luminosité
de luminosité 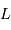 , observé pendant une durée
, observé pendant une durée 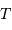 , apporte une énergie
, apporte une énergie 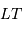 . Ce rayonnement est véhiculé par un nombre moyen de photons
. Ce rayonnement est véhiculé par un nombre moyen de photons 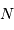 obéissant à :
obéissant à :
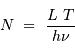
La discrétisation du flux en quanta d'énergie implique que le nombre de photons arrivant par intervalle de temps fluctue autour de cette valeur moyenne.
Extrapolation aux grandes valeurs
Pour les grandes valeurs de 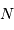 , on peut montrer que cette loi se confond très rapidement avec la gaussienne :
, on peut montrer que cette loi se confond très rapidement avec la gaussienne :
![p(n) \ \propto \ \exp \left[ - {(n-N)^2 \over 2 N}\right]](../pages_analyser/equations_bruit-poisson/equation32.png)
On en conclut alors, en se basant sur la statistique gaussienne, que pour une valeur moyenne 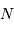 , l'écart-type vaut
, l'écart-type vaut 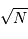 .
.
Il en résulte un point important : lorsque 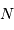 croît, l'écart-type croît, mais le rapport écart-type/moyenne du signal décroît.
croît, l'écart-type croît, mais le rapport écart-type/moyenne du signal décroît.
Distribution de Poisson
A l'aide de l'appliquette : tracer une distribution de Poisson, et identifier les variations majeures lorsque la moyenne 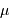 varie.
varie.

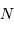 quanta par unité de temps est attendue, un détecteur idéal (rendement unité) en comptera un nombre plus ou moins voisin de
quanta par unité de temps est attendue, un détecteur idéal (rendement unité) en comptera un nombre plus ou moins voisin de 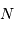 . La distribution des valeurs dépend du nombre N :
10,
100,
1000.
Plus
. La distribution des valeurs dépend du nombre N :
10,
100,
1000.
Plus 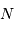 est grand, plus la distribution apparaît piquée en valeur relative, quand bien même elle est plus étalée en valeur absolue.
est grand, plus la distribution apparaît piquée en valeur relative, quand bien même elle est plus étalée en valeur absolue.




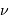 de luminosité
de luminosité 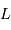 , observé pendant une durée
, observé pendant une durée 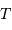 , apporte une énergie
, apporte une énergie 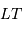 . Ce rayonnement est véhiculé par un nombre moyen de photons
. Ce rayonnement est véhiculé par un nombre moyen de photons 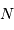 obéissant à :
obéissant à :
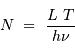
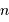 photons lorsque
photons lorsque 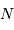 sont attendus en moyenne s'écrit :
sont attendus en moyenne s'écrit :
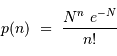
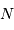 .
Il faut retenir que :
.
Il faut retenir que :
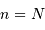 .
.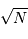 .
.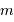 parties, suffisamment petites pour assurer qu'un seul photon peut arriver pendant l'intervalle de temps
parties, suffisamment petites pour assurer qu'un seul photon peut arriver pendant l'intervalle de temps 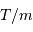 , on peut estimer la probabilité de voir arriver
, on peut estimer la probabilité de voir arriver 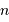 photons, en les rangeant dans les
photons, en les rangeant dans les 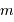 cases.
cases.
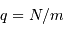 , et la probabilité opposée
, et la probabilité opposée 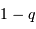 . Comme il y a
. Comme il y a 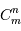 façons de ranger
façons de ranger 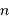 photons dans les
photons dans les 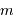 cases, on obtient finalement en développant le coefficient de combinaison :
cases, on obtient finalement en développant le coefficient de combinaison :
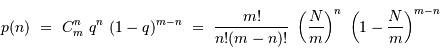
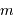 d'intervalles, on retrouve la loi énoncée :
d'intervalles, on retrouve la loi énoncée :
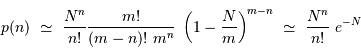
 grand et
grand et  :
:
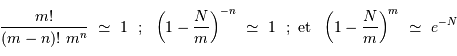
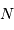 , on
, on ![p(n) \ \propto \ \exp \left[ - {(n-N)^2 \over 2 N}\right]](../pages_analyser/equations_bruit-poisson/equation32.png)
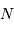 , l'écart-type vaut
, l'écart-type vaut 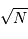 .
.
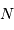 croît, l'écart-type croît, mais le rapport écart-type/moyenne du signal décroît.
croît, l'écart-type croît, mais le rapport écart-type/moyenne du signal décroît.
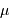 varie.
varie.
