Dans ce chapitre...
Dans ce chapitre...
... nous retracerons l'histoire des découvertes concernant la lumière. De l'Antiquité au XXe siècle, comment est-on passé d'une optique géométrique et corpusculaire à une optique ondulatoire, puis à une théorie plus complète, intégrant les deux descriptions ?
Nous établirons également quelques propriétés de la lumière, en décrivant ce qu'est une onde et présentant ce qu'est un photon.
Puis nous dessinerons les contours de l'optique géométrique, afin de fixer le cadre dans lequel nous travaillerons jusqu'à la fin de ce cours.
Voici l'histoire de la lumière !
Crédit :
B. Mollier
Durant l'antiquité
L'histoire de l'optique commence dès l'Antiquité. Les notions de rayons lumineux ainsi que les lois de la réflexion sont déjà connues d'Euclide et de Ptolémée.
Le XVIIe siècle et la redécouverte des lois de la réflexion et de la réfraction
Il faudra cependant attendre plusieurs siècles et le mathématicien et physicien arabe Alhazen pour que soient énoncées les lois de la réfraction. Elles seront redécouvertes en Europe par le physicien hollandais W. Snell (1621) puis par le français René Descartes en 1637. Il est amusant de voir que ces lois sont appelées lois de Snell partout dans le monde, sauf en France, où elles sont appelées lois de Descartes. Vous avez dit chauvinisme ? Débat stérile puisqu'elles avaient été découvertes six siècles avant eux. De plus, elles avaient déjà été publiées en Europe par le britannique Roger Bacon au XIIIe siècle.
La théorie corpusculaire et les premiers instruments astronomiques
galilee-florence

Buste de Galilée, sur sa tombe dans l'église Santa Croce, à Florence
Crédit :
B. Mollier
Les premiers instruments optiques pour l'astronomie apparaissent aux XVIIe siècle avec l'utilisation de la lunette par Galilée en 1609 puis l'amélioration du télescope par Isaac Newton en 1671. Le XVIIe siècle voit donc se développer l'optique géométrique ainsi qu'une description corpusculaire de la lumière, portée notamment par Newton. Les sources lumineuses émettent des particules de lumière qui sont réfléchies par les miroirs et traversent les milieux transparents à différentes vitesses. De cette description, Fermat tirera le principe de moindre temps pour expliquer les phénomènes de réfraction. La lumière emprunte le chemin le plus rapide pour aller de l'émetteur au récepteur. À cette même époque, Newton réalise les premières expériences de décomposition de la lumière et en déduit que la lumière blanche est composée de la superposition de lumières colorées.
Le XIXe siècle et la théorie ondulatoire
Parallèlement, le physicien néerlandais Christiaan Huygens développe, en 1678, une théorie ondulatoire de la lumière. Selon lui, elle serait constituée d'ondes sphériques émises en différents points. La lumière réelle en serait l'enveloppe. Avec sa théorie, il parvient à expliquer la réflexion et la réfraction.
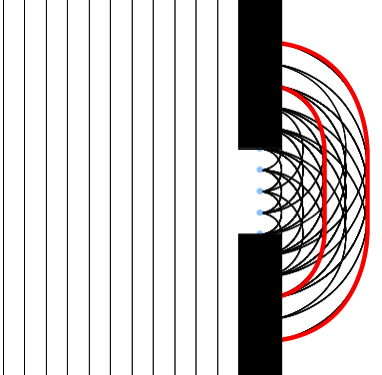
Ondelettes de Huygens, dans le cas de la diffraction par une fente. La lumière arrive par la gauche. Elle est dite plane car les surfaces des ondelettes sont des plans. En franchissant l'obstacle, la lumière se diffracte : les surfaces ne sont plus planes.
Crédit :
ASM/B. Mollier
Ce modèle ne sera repris qu'au XIXe siècle, où la théorie ondulatoire permet à Thomas Young d'expliquer le phénomène d'interférence, ainsi qu'à Augustin Fresnel de développer la théorie de la diffraction. James Clerk Maxwell termine le travail en construisant une théorie de l'électromagnétisme. La lumière est désormais une onde électromagnétique, de fréquence de l'ordre de 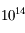 Hz pour sa partie visible, se propageant à la vitesse
Hz pour sa partie visible, se propageant à la vitesse 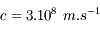 .
.
Le XXe siècle : et si c'était un peu des deux ?
Cependant, quelques phénomènes résistent encore à cette description : l'effet photoélectrique et l'émission du corps noir. Albert Einstein, dans un article publié en 1905, remet au goût du jour la théorie corpusculaire en introduisant la notion de photon, un grain de lumière, d'énergie 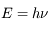 , où
, où 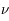 est la fréquence de l'onde électromagnétique précédemment introduite, et
est la fréquence de l'onde électromagnétique précédemment introduite, et 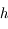 une constante, qui portera le nom du physicien Planck. Dans cet article, il parviendra à expliquer l'un des phénomènes encore mystérieux, l'effet photoélectrique. Il est d'ailleurs amusant de rappeler que c'est pour cet article que le père de la relativité recevra le prix Nobel. Le second phénomène, l'émission du corps noir, sera alors résolu grâce à ce nouveau modèle, par Max Planck et Einstein.
une constante, qui portera le nom du physicien Planck. Dans cet article, il parviendra à expliquer l'un des phénomènes encore mystérieux, l'effet photoélectrique. Il est d'ailleurs amusant de rappeler que c'est pour cet article que le père de la relativité recevra le prix Nobel. Le second phénomène, l'émission du corps noir, sera alors résolu grâce à ce nouveau modèle, par Max Planck et Einstein.
Onde ou corpuscule ? En 1924, Louis de Broglie concilie les deux approches en parlant de dualité onde corpuscule. Les deux théories, loin de s'opposer, se complètent. Les dernières contradictions sont levées par la théorie de l'électrodynamique quantique esquissée par Richard Feynman, au cours des années 1950.
 Qu'est-ce que la lumière ?
Qu'est-ce que la lumière ?
Nous venons de voir que la description de la lumière a évolué au cours du temps : tantôt une onde, tantôt un corpuscule, tantôt les deux à la fois.
Néanmoins, pour nombre de phénomènes que nous étudierons dans la suite de ce cours, la connaissance de la nature de la lumière n'est pas nécessaire.
Afin de satisfaire la curiosité du lecteur, je vais toutefois présenter quelques propriétés de la lumière.
Qu'est-ce que la lumière ?
Onde ou corpuscule ?
Crédit :
B. Mollier
Les trois pages qui suivent sont inspirées du cours du professeur Tadashi Tokieda à l'Ecole de Cargese "Transit, eclipses, occultations et phénomènes rasants".
 Qu'est-ce qu'une onde ?
Qu'est-ce qu'une onde ?
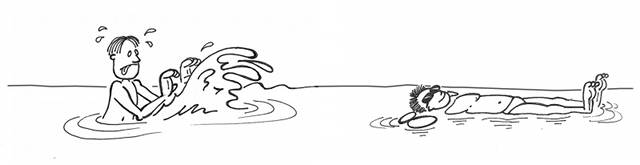
Dans une piscine, un farceur veut éclabousser son copain. Comment s'y prend-il ?
Comment éclabousser un ami ?

Crédit :
B. Mollier
Une poussée directe projette de l'eau... mais pas assez loin. Le copain est toujours sec.
Pas comme ça...
Crédit :
B. Mollier
Par contre, s'il excite une onde, en agitant régulièrement les bras, le tour est joué !
... mais avec une onde !

Crédit :
B. Mollier
Le train de vagues créé est une onde. Le farceur a communiqué de l'énergie à l'eau, en la mettant en mouvement de haut en bas, et celle-ci s'est propagée jusqu'au malheureux.
Tiens, c'est intéressant. Un enfant a oublié son canard en plastique dans la piscine. Notre victime pourra se consoler avec ce jouet, qui ira tout droit jusqu'à lui, porté par les vagues. Et bien... non. Dommage pour lui, mais si on observe le canard, certes il oscille de haut en bas, mais il n'avance pas dans la piscine.
Un canard enchainé ?

Crédit :
B. Mollier
C'est une propriété importante des ondes. Le transport d'énergie se fait sans transport de matière.
 Définition
Définition
Une onde est un phénomène de propagation ordonnée d'énergie, sans transport de matière.
 Propriétés
Propriétés
- Remarque, le terme "ordonné" employé ici permet de distinguer les phénomènes propagatifs de type onde, des phénomènes de diffusion de la chaleur, où une énergie est également transmise sans transport de matière, mais par des mouvements désordonnés des molécules.
- Une onde se propage à partir de la source (le farceur) dans toutes les directions qui lui sont offertes (la piscine).
- La perturbation se transmet de proche en proche avec transfert d'énergie (le canard oscille) mais sans transport de matière (le canard n'avance pas).
- La vitesse de propagation d'une onde est une propriété du milieu dans lequel elle se propage. Dans un bain de mercure (si on aime ça !) les vagues n'iraient pas à la même vitesse.
J'ai cité l'exemple des vagues à la surface de la piscine, mais il existe bien d'autres exemples d'ondes :
- La propagation d'une perturbation le long d'une corde tendue. Si on donne un coup sur un bout de la corde, on constate que cette perturbation se propage jusqu'à l'autre bout de la corde. On peut noter aussi que plus celle-ci est tendue, plus l'onde se propage rapidement. On retrouve le fait que la vitesse de propagation est une caractéristique du milieu.
- Plus classique, la houle est également une onde.
- Le son est une onde acoustique se propageant dans l'air (à
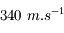 à température ambiante et à pression atmosphérique), ou dans les autres milieux (eau, solides...).
à température ambiante et à pression atmosphérique), ou dans les autres milieux (eau, solides...).
À noter que toutes les ondes précédemment mentionnées nécessitent un support pour se propager. L'espace étant vide, le son ne peut s'y propager. Les bruits d'explosions dans Star Wars ne sont donc que pure fiction.
 L'onde lumineuse : une onde électromagnétique
L'onde lumineuse : une onde électromagnétique
De la même façon que dans l'air on peut créer une onde sonore en perturbant mécaniquement le milieu, on crée une onde électromagnétique en secouant une charge électrique (un électron par exemple) dans le vide. C'est une onde lumineuse.
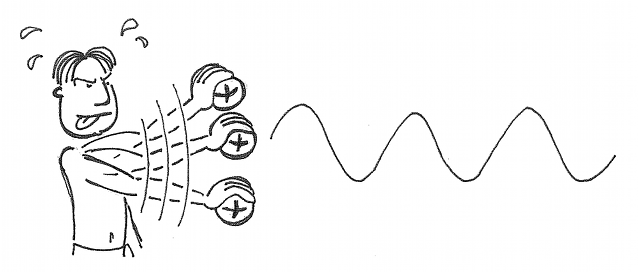
Crédit :
B. Mollier
Le dessin ici est trompeur, car l'onde est rayonnée dans toutes les directions. Dans la piscine, les vagues se propageaient tout autour de notre farceur, en faisant des ronds dans l'eau.
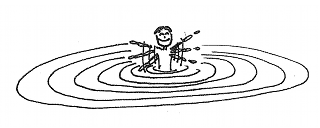
Crédit :
B. Mollier
Notre charge crée de la même manière des ondes sphériques autour d'elle. À noter cependant que la puissance rayonnée dépendra de la direction dans ce cas particulier.
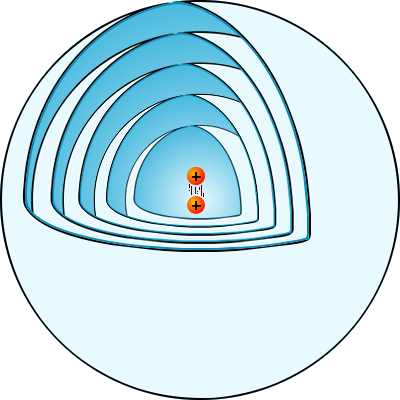
Crédit :
ASM/B. Mollier
 Remarque
Remarque
À l'inverse des ondes citées jusqu'à présent, l'onde électromagnétique n'a pas besoin de support pour se propager. Elle peut se déplacer dans le vide. C'est d'ailleurs comme ça qu'on peut voir les étoiles. Cela a dérouté les physiciens pendant de nombreuses années, et ils avaient introduit un support, de nature inconnue, appelé éther pour expliquer la propagation des ondes lumineuses. C'était un fluide qui emplissait tout l'espace. Or, comme la Terre se déplaçait dedans, il devait exister des vents d'éther, se traduisant par une vitesse de propagation de la lumière différente selon la direction d'où elle venait. Deux physiciens, Michelson et Morlay, ont alors mis au point un instrument très précis, un interféromètre, pour mesurer la vitesse de la lumière dans plusieurs directions. Ils n'ont jamais trouvé de différence. Michelson a alors considéré son expérience comme un échec, remettant en cause sa précision. L'explication était tout autre. L'éther n'existait pas, et la vitesse de la lumière constante, qu'elle que soit la direction. Le principe de relativité restreinte était né sous la plume d'Einstein.
 La célérité de la lumière dans le vide
La célérité de la lumière dans le vide
Une onde électromagnétique se propage dans le vide toujours à la même vitesse.
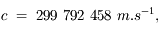
soit presque 8 tours de la Terre en une seconde !
Vous avez dit toujours ? Oui, toujours ! dans le vide.
 Remarques
Remarques
- Quel que soit le référentiel où on l'observe (au repos dans un laboratoire, dans une fusée...), elle se déplace toujours à
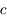 . De cette constatation naîtra la théorie de la relativité restreinte.
. De cette constatation naîtra la théorie de la relativité restreinte. - Et dans un milieu transparent, donc hors du vide, elle ne se propage pas moins vite ? Oui et non. Mais nous y reviendrons.
Vitesse de la lumière
Dans le vide, la lumière se propage à la vitesse
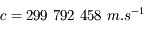
.
Crédit :
B. Mollier
 Römer
Römer
En 1676, à l'Observatoire de Paris, Olaus Römer, physicien danois, est le premier à émettre l'hypothèse du caractère fini de la vitesse de la lumière. Il explique ainsi les variations de la récurrence des éclipses du satellite jovien Io. Elles variaient en effet de plusieurs minutes par rapport aux éphémérides. De ses mesures, il déduit que la lumière se propage à 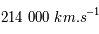 (avec une erreur de l'ordre de 30 % par rapport à la valeur mesurée aujourd'hui).
(avec une erreur de l'ordre de 30 % par rapport à la valeur mesurée aujourd'hui).
 Fizeau
Fizeau
En 1849, Fizeau mesure à son tour la vitesse de la lumière, à l'aide d'un dispositif constitué d'une roue dentée, située à Suresnes et d'un miroir situé à quelques kilomètres de là, à Montparnasse. La lumière passe entre deux dents à l'aller se réfléchit sur le miroir puis revient. L'exercice consiste alors à trouver la vitesse de la roue qui permet à la lumière réfléchie de passer entre les deux dents suivantes. La donnée de cette vitesse ainsi que de la distance de la roue au miroir donne la valeur de 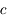 .
.
 Foucault
Foucault
Léon Foucault

Crédit :
Bibliothèque de l'Observatoire de Paris
Foucault réalisera, un an après, une expérience proche, permettant de mesurer la vitesse dans différents milieux transparents, comme l'eau. Il en déduira que la lumière se propage moins vite dans l'eau que dans l'air, mettant un terme à la théorie corpusculaire, qui prédisait le résultat inverse.
 Michelson, Morlay, Einstein...
Michelson, Morlay, Einstein...
Albert Einstein

Crédit :
B. Mollier
En 1887, Michelson et Morlay prouvent que la lumière se propage à la même vitesse dans toutes les directions et que le mouvement de la Terre dans l'espace n'influence pas cette valeur. Mais c'est Albert Einstein qui trouvera l'interprétation correcte de cette expérience : la vitesse de la lumière est constante et égale à 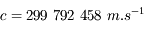 , et ce, dans n'importe quel référentiel.
, et ce, dans n'importe quel référentiel.
 Complément : La vitesse des neutrinos
Complément : La vitesse des neutrinos
En 2011, une équipe du CERN avait annoncé avoir enregistré des neutrinos (des particules neutres, très légères, et n'interagissant que très peu avec la matière) se déplaçant plus vite que la lumière. Cela rentrait en contradiction avec la théorie de la relativité restreinte, qui énonce qu'aucune particule, ne peut se déplacer plus vite que la lumière dans le vide. Après de nombreuses vérifications, un biais dans la mesure a été détecté. L'erreur de mesure était due à une mauvaise connexion d'une balise GPS.
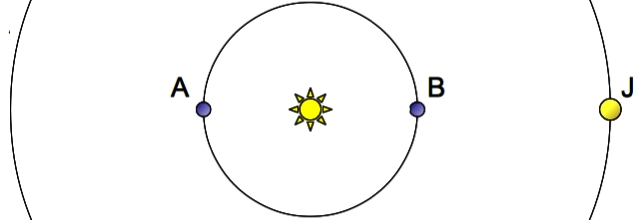
 Expérience de Olaüs Römer
Expérience de Olaüs Römer
En fonction de la position de la Terre (en A ou en B), il existe un décalage de 996 secondes dans les prédictions de l'heure de l'éclipse du satellite Io de Jupiter (en J).
Expérience de Römer
Crédit :
ASM/B. Mollier
Question 1)
Calculer la vitesse de la lumière.
La distance Terre-Soleil est de 1 unité astronomique, et celle entre Jupiter et le Soleil est de 5 unités astronomiques.
 Période et fréquence temporelles
Période et fréquence temporelles
Sautons à nouveau dans la piscine. Notre farceur crée une vague à chaque fois que ses bras font un mouvement de haut en bas puis de bas en haut. S'il agite doucement les bras, la durée entre deux vagues sera longue. Par contre, s'il les agite rapidement, cette durée se raccourcit.
Période
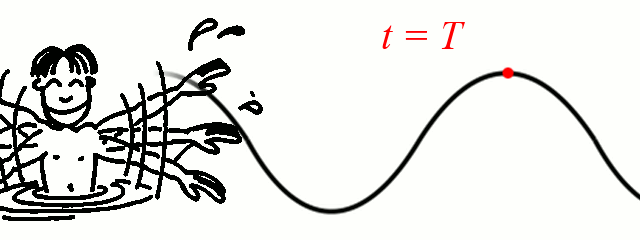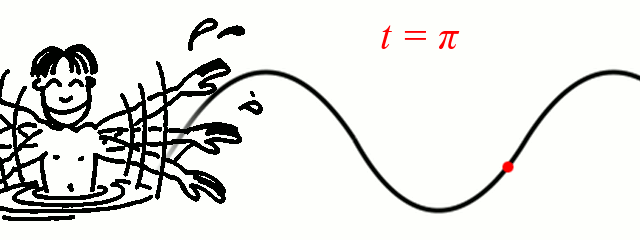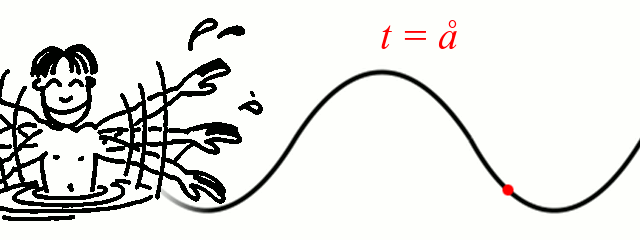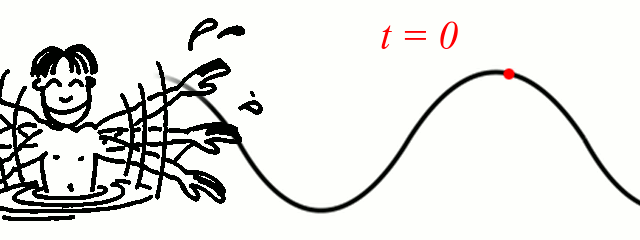
La période temporelle est le temps qui s'écoule entre le passage de deux maxima.
Crédit :
B. Mollier
Nous venons de mettre en évidence la période temporelle d'une onde (que l'on notera 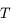 ). Dans le cas des vagues, elle est de l'ordre d'une seconde. Inversement, on voit passer une vague par seconde environ. Un peu plus si le temps entre deux vagues est plus court, un peu moins, s'il est plus long. C'est ce qu'on appelle la fréquence (notée
). Dans le cas des vagues, elle est de l'ordre d'une seconde. Inversement, on voit passer une vague par seconde environ. Un peu plus si le temps entre deux vagues est plus court, un peu moins, s'il est plus long. C'est ce qu'on appelle la fréquence (notée 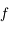 ou
ou 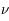 ). Elle est définit comme l'inverse de la période temporelle.
). Elle est définit comme l'inverse de la période temporelle.
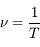
Elle s'exprime en Hertz (Hz). 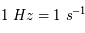 .
.
 Période spatiale et longueur d'onde
Période spatiale et longueur d'onde
On s'intéresse maintenant non plus au temps séparant deux vagues, mais à la distance entre deux sommets de vagues. Cette distance est appelée longueur d'onde, et souvent notée 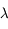 . Elle s'exprime en mètre.
. Elle s'exprime en mètre.
Longueur d'onde
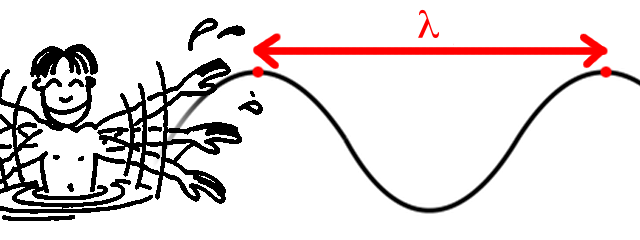
La période spatiale est la distance qui sépare deux maxima.
Crédit :
B. Mollier
Si notre farceur agite plus vite les bras, on sent bien qu'il y aura plus de vagues, et que la distance séparant deux d'entre elles sera plus courte. Il existe donc une relation entre la fréquence et la longueur d'onde.
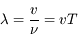
On remarque donc que, à période 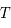 fixée, si la vitesse augmente, la longueur d'onde augmente. Les vagues fuient plus vite et donc la distance entre elles grandit.
fixée, si la vitesse augmente, la longueur d'onde augmente. Les vagues fuient plus vite et donc la distance entre elles grandit.
 Un électron qui s'agite, qui s'agite...
Un électron qui s'agite, qui s'agite...
Le farceur peut agiter plus ou moins vite les bras. Il en est de même pour notre charge électrique. On peut la secouer très doucement, de l'ordre du Hertz. Elle créera alors une onde radio. Si on l'excite très vite, de l'ordre de un million de milliards de fois par seconde, c'est une onde lumineuse visible qui naîtra. Encore plus vite, et ce seront des rayons X et 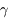 qui seront générés.
qui seront générés.
 Les domaines de fréquences luminueuses
Les domaines de fréquences luminueuses
La fréquence des ondes lumineuses peut donc varier sur plusieurs ordres de grandeur, allant de la radio aux rayons 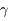 en passant par le visible. Pourtant, ce sont tous la manifestation d'un même phénomène, la propagation d'une onde électromagnétique. Seule la fréquence varie.
en passant par le visible. Pourtant, ce sont tous la manifestation d'un même phénomène, la propagation d'une onde électromagnétique. Seule la fréquence varie.
Si ces ondes lumineuses ne sont pas toutes regroupées sous la même appellation, c'est en partie pour des raisons historiques (on ne savait pas encore que c'était la même chose), et en partie pour des raisons instrumentales, car les outils pour les détecter ne sont pas les mêmes. On utilise parfois des antennes, parfois des miroirs et des capteurs CCD, parfois des lames de silicium...
L'astronomie est un domaine très riche, où toutes ces fréquences sont intéressantes à étudier, car elles nous renseignent sur des phénomènes très variés et des objets très différents. Le tableau suivant présente les différents domaines de longueurs d'onde ainsi que les phénomènes les produisant.
Les différents domaines spectraux
| Domaine spectral | Longueur d'onde (en m) | Fréquence (en Hz) | Instruments | Sources |
| Ondes radio | 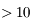 | 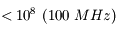 | Réseau décamétrique de Nançay | Nuages froids, aurores polaires. |
| Ondes radio | 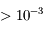 | 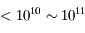 | Radiotélescope de Nançay | Hydrogène neutre (raie à 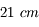 )... )... |
| Submillimétrique | 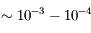 | 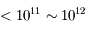 | Observatoire du plateau de Bures | Fond diffus cosmologique, objets/poussières froids... |
| Infrarouge | 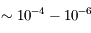 | 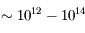 | VLT, CHARA, Keck, Spitzer | Étoiles, planètes, poussières... |
| Visible | 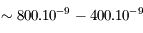 | 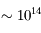 | Hubble, HARPS, Soho... | Étoiles, Soleil, planètes, nébuleuses, trous noirs... |
| Ultraviolet | 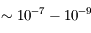 | 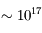 | Soho | Soleil, étoiles, trous noirs |
| Rayons X | 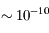 | 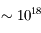 | XMM, Chandra... | Étoiles binaires en interaction, trous noirs... |
| Rayons γ | 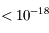 | 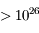 | Fermi | Sursauts gamma, trous noirs |
Le spectre électromagnétique

Le spectre électromagnétique s'étend de la radio aux rayons gammas. À l'aide de différents instruments (de gauche à droite : Le réseau décamétrique de Nançay, le télescope décimétrique de Nançay, l'interféromètre submillimétrique du plateau de Bure, le satellite Planck, le satellite infrarouge Spitzer, le VLT, le télescope spatial Hubble, l'observatoire X européen XMM-Newton, le satellite gamma Fermi), permet d'observer des objets aussi divers que (de gauche à droite) des galaxies en collisions, le fond diffus cosmologique, la poussière dans une galaxie, des nébuleuses diffuses, le Soleil, la Voie Lactée.
Crédit :
B. Mollier (+NASA / ESA / CNES / IRAM)
La Voie Lactée à différentes longueurs d'onde

La Voie Lactée observée à différentes longueurs d'onde, de la radio (en haut) aux rayons gamma en bas.
Crédit :
NASA
 Propagation à travers un milieu
Propagation à travers un milieu
Lorsque la lumière se propage dans un milieu (air, eau, verre...), elle interagit avec celui-ci. Ce dernier modifie les propriétés de la lumière. Il peut changer sa vitesse, lui prendre de l'énergie (plus rare, lui en donner).
Dans certains milieux, tel le verre, la vitesse est plus importante pour le rouge que pour le bleu. Ce phénomène est appelé dispersion. Il est utilisé, depuis Newton, dans les prismes, pour décomposer la lumière.
Décomposition de la lumière

Un prisme utilise la propriété dispersive du verre pour décomposer la lumière. Dans tous les phénomènes dispersifs dus à la réfraction, le rouge sera moins dévié que le bleu. C'est comme ça que l'on distingue les phénomènes réfractifs des phénomènes diffractifs.
Crédit :
B. Mollier (fortement inspiré de la pochette de l'album "Dark side of the moon" des Pink Floyd.)
L'intensité lumineuse peut décroître dans les milieux. C'est le phénomène d'absorption (exemple : les lunettes de soleil). Elle peut également croître dans les milieux amplificateurs. Ces milieux sont utilisés dans les lasers.
 Milieu transparent, homogène, isotrope
Milieu transparent, homogène, isotrope
Dans la suite, ce cours se limitera à l'étude des milieux homogènes transparents et isotropes (HTI).
- Transparent : le terme transparent fait référence ici à un milieu non absorbant.
- Homogène : les propriétés du milieu sont les mêmes en tout point de l'espace.
- Isotrope : les propriétés du milieu sont les mêmes dans toutes les directions.
 Indice optique d'un milieu HTI
Indice optique d'un milieu HTI
Nous venons de le voir, dans un milieu HTI (MHTI), la lumière se propage moins vite que dans le vide. On définit l'indice 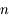 du milieu comme étant le rapport de la vitesse de la lumière dans le vide sur sa vitesse
du milieu comme étant le rapport de la vitesse de la lumière dans le vide sur sa vitesse 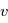 dans le milieu.
dans le milieu.
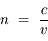
La vitesse dans un milieu HTI étant toujours inférieure à celle dans le vide, 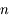 est toujours supérieur à 1.
est toujours supérieur à 1.
Propagation dans un MHTI
La vitesse dans un milieu HTI étant toujours inférieure à celle dans le vide, l'indice
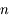
est toujours supérieur à 1.
Crédit :
B. Mollier
Les MHTI étant généralement dispersifs, l'indice 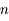 dépend de la longueur d'onde.
dépend de la longueur d'onde.
Indices de différents milieux
| Milieux | Indices |
| Vide | 1 |
| Air | 1,00029 |
| Eau | 1,33 |
| Verre crown | 1,52 |
| Verre flint | 1,67 |
Le milieu est d'autant plus réfringent qu'augmente 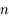 .
.
 Indices et célérité de la lumière
Indices et célérité de la lumière
Une molécule d'eau est composée d'un atome d'oxygène et de deux atomes d'hydrogène : 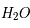 . Parfois, l'atome d'hydrogène est remplacé par son isotope stable, le deutérium. Ce dernier est composé d'un proton et d'un neutron. Il est deux fois plus lourd que l'hydrogène. Cette molécule
. Parfois, l'atome d'hydrogène est remplacé par son isotope stable, le deutérium. Ce dernier est composé d'un proton et d'un neutron. Il est deux fois plus lourd que l'hydrogène. Cette molécule 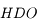 est alors appelée eau semi-lourde. L'eau lourde, quant à elle, est constituée de deux atomes de deutérium :
est alors appelée eau semi-lourde. L'eau lourde, quant à elle, est constituée de deux atomes de deutérium : 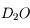 .
.
L’eau lourde est utilisée dans certains réacteurs nucléaires comme modérateur de neutrons. Son but est ralentir les neutrons issus de réactions de fission nucléaire. Les neutrons ralentis ont alors une probabilité plus élevée de provoquer de nouvelles fissions de noyaux d'uranium, permettant ainsi la réaction en chaîne.
Question 1)
L'indice optique de l'eau légère est noté 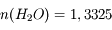 . Calculer la vitesse de la lumière dans cette eau.
. Calculer la vitesse de la lumière dans cette eau.
Question 2)
La vitesse de la lumière dans l'eau lourde 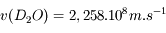 . Calculer son indice optique.
. Calculer son indice optique.
Question 3)
Laquelle de ces 2 eaux est la plus réfringente ? Où la lumière se déplace-t-elle le plus vite ?
 L'effet photoélectrique
L'effet photoélectrique
Tout ce que nous venons de dire permet de décrire beaucoup de phénomènes optiques, mais pas l'effet photoélectrique. Quel est ce phénomène qui échappe encore à notre description ?
L'effet photoélectrique se manifeste quand on éclaire un métal avec un rayonnement UV. Des électrons sont alors arrachés du métal à cause de cette lumière. Pour que les électrons soient arrachés, il faut leur communiquer de l'énergie en quantité suffisante. Sous un certain seuil d'énergie, les électrons ne pourront pas quitter la plaque de métal. Mais au-dessus d'un certain seuil, ils pourront "sauter la barrière" et quitter le métal.
Intuitivement, on peut se dire que plus l'intensité de la lumière est importante, plus grande sera l'énergie apportée aux électrons. Au dessus d'un certain flux lumineux, l'effet photoélectrique se manifestera.
Il n'en est rien. Si on éclaire la plaque avec de la lumière rouge, verte ou bleue, quelle que soit l'intensité du flux, aucun électron n'est jamais émis. Par contre, dès qu'on descend en longueur d'onde, et qu'on atteint l'ultraviolet, l'effet photoélectrique apparaît. Même à faible flux lumineux ! Ça n'est pas intuitif du tout !
Effet photoélectrique

L'effet photoélectrique ne dépend pas de l'intensité du flux lumineux, mais uniquement de la longueur d'onde. Cet effet ne s'explique pas en optique ondulatoire, mais uniquement en mécanique quantique.
Crédit :
B. Mollier
 L'hypothèse du photon
L'hypothèse du photon
Comment expliquer ceci ? Il faut revenir à l'hypothèse corpusculaire. La lumière est vue comme un flux de petits grains, qu'on appellera photons, chacun transportant une petite quantité d'énergie, un quantum d'énergie.
En quoi ça change ? Et bien, d'une part l'énergie totale est proportionnelle au nombre de photon. Plus il y a de photons, plus on apporte d'énergie. Mais aucun photon, pris individuellement, ne possède l'énergie suffisante pour faire "sauter" un électron. Sauf en dessous d'une certaine longueur d'onde. Là chaque photon, même en très petit nombre, peut arracher un électron. On en déduit que l'énergie des photons est inversement proportionnelle à la longueur d'onde, ou, de manière équivalente, proportionnelle à la fréquence.
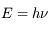
La constante de proportionnalité  est appelée constante de Planck, et vaut
est appelée constante de Planck, et vaut 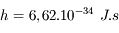 .
.
Effet photoélectrique
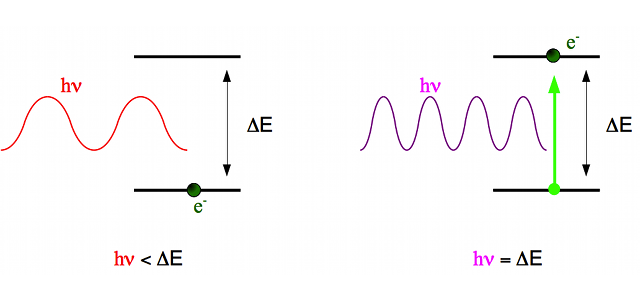
L'électron ne peut changer de niveau que si le photon incident possède sensiblement la même énergie que le niveau à "sauter".
Crédit :
ASM/B. Mollier
 Une petite expérience...
Une petite expérience...
Réalisons une expérience. Plaçons nous dans le noir et observons le pinceau lumineux rouge issu d'un laser hélium-néon. La poussière flottant dans la pièce diffuse la lumière de celui-ci, nous permettant d'observer la trajectoire du pinceau lumineux. On constate que celui-ci est rectiligne.
Les rayons lumineux traversant les rideaux, le matin, ont également l'air rectiligne.
En reproduisant ces expériences avec différentes sources et différents milieux, on constaterait toujours que la lumière se propage en ligne droite dans l'espace.
Étoile guide laser

Un rayon laser sert d'étoile guide pour l'optique adaptative du VLT. Il se propage en ligne droite. On ne le voit sur cette image que parce que de la poussière en diffuse une partie.
Crédit :
ESO
 Propriété
Propriété
La lumière se propage en ligne droite dans un MHTI.
 Remarque
Remarque
Remarquons que ceci n'est plus vrai dès lors que le milieu n'est plus homogène. Nous aborderons brièvement ce phénomène dans le cas des mirages (chapitre suivant) et en toute fin pour les problèmes de turbulence atmosphérique.
 Isoler un rayon lumineux ?
Isoler un rayon lumineux ?
Reprenons le laser et observons son faisceau. Pouvons-nous réduire de la taille de celui-ci afin de n'obtenir qu'un seul rayon lumineux ?
Pour cela, plaçons un diaphragme devant ce premier. Si on diminue le rayon de celui-ci, le faisceau voit son diamètre diminuer. On observe sur un écran que la tache que fait le laser diminue, mais reste uniformément éclairée.
Mais lorsque le rayon du diaphragme atteint des valeurs de l'ordre du micromètre, le pinceau se met à diverger, la tache grossit et on voit apparaître des anneaux autour de celle-ci. Nous venons de mettre en évidence le phénomène de diffraction. On y reviendra tout à la fin. Cela constitue un écart à la théorie de propagation rectiligne de la lumière dans les MHTI.
Isolons un rayon lumineux

Lorsque l'on diminue le diamètre du diaphragme, l'épaisseur du faisceau diminue d'abord, avant de diverger. C'est le phénomène de diffraction.
Crédit :
ASM/B. Mollier
 Qu'est-ce qu'une théorie en physique ?
Qu'est-ce qu'une théorie en physique ?
Profitons-en ici pour préciser que nombre de théories en physique (mais aussi en chimie, en biologie...) ne sont valides que sous certaines hypothèses et sous certaines conditions. Elles sont valables dans des "boites", c'est-à-dire dans un cadre théorique donné. Si on sort de cette boite, la théorie n'est plus valide. Elle peut être remplacée par une loi plus générale, plus complète, souvent plus complexe, si, bien sûr, elle a été découverte. Un exemple "classique", est la théorie de la mécanique newtonienne qui fonctionne aux faibles vitesses. Mais dès que l'on se rapproche de la vitesse de la lumière, cette théorie ne fonctionne plus, et il faut passer à une théorie plus générale : la relativité restreinte d'Einstein.
 Le cadre de l'optique géométrique
Le cadre de l'optique géométrique
Notre conclusion ici est que la propagation rectiligne de la lumière est une loi limite, valable quand les longueurs d'onde sont faibles devant les dimensions caractéristiques de notre système. C'est le cadre de l'optique géométrique.
 Et maintenant...
Et maintenant...
On a vu que la lumière visible possède des longueurs d'onde caractéristiques inférieures au micron. Que ce soit dans les télescopes ou les appareils photos, les diamètres des diaphragmes sont bien supérieurs à la longueur d'onde de la lumière visible. Nous pourrons donc toujours utiliser cette approximation.
 Le rayon lumineux
Le rayon lumineux
Nous nous plaçons dans les conditions où la lumière se propage en ligne droite comme le ferait un ensemble de particules matérielles (les photons) libres. Les trajectoires de ces particules constituent les rayons lumineux.
La notion de rayon lumineux est illustrée par un pinceau lumineux cylindrique obtenu avec un petit diaphragme (mais 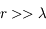 ).
).
 Propriétés
Propriétés
- Dans un MHTI, dans le cas des 2 sources de lumière par exemple, les rayons lumineux se propagent indépendamment les uns des autres.
- Principe de moindre temps. Dans un MHTI, le chemin effectivement parcouru par la lumière est celui qui rend le temps de parcours minimal. Dans un MHTI, c'est donc la ligne droite. C'est ce qu'on appelle aussi le principe de Fermat.
- Il en résulte que, pour aller d'un point B à un point A, la lumière reprendra exactement le même chemin que celui emprunté pour aller de A à B. Il s'agit du principe de retour inverse de la lumière.
Le retour inverse de la lumière
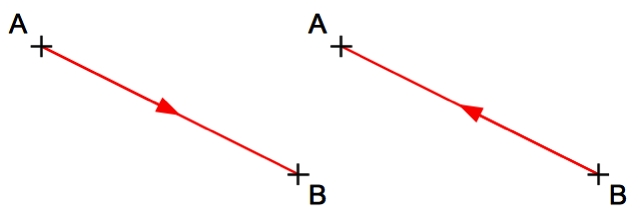
Un rayon lumineux empruntera le même chemin pour aller de A à B que pour revenir de B à A. Il s'agit du principe de retour inverse de la lumière.
Crédit :
ASM/B. Mollier
 Éclipse solaire
Éclipse solaire
Une éclipse totale de Soleil a lieu le 13 novembre 2012. Vous pouvez consulter le site de l'IMCCE pour obtenir les suivantes. Pourquoi, lors de ces phénomènes, existe-t-il des zones d'ombre et de pénombre ? Examinons cela.
Question 1)
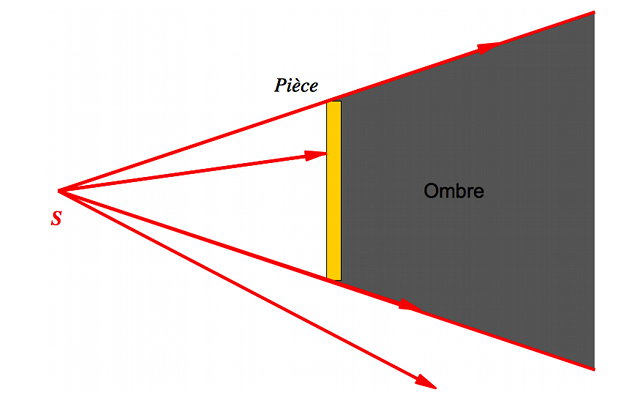
On considère une source ponctuelle. On place une pièce devant. Tracer l'ombre de la pièce.
Utilisez la propriété que la lumière se propage en ligne droite dans un MHTI.
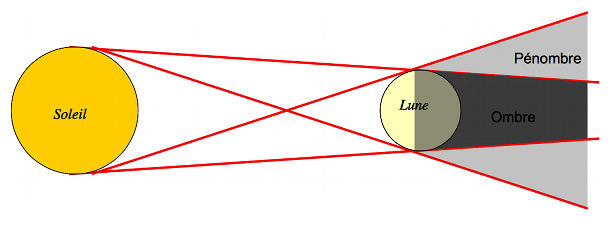
Question 2)
On considère cette fois ci la source étendue que constitue le Soleil. Notre pièce est remplacée par la Lune. Tracer la zone d'ombre, c'est-à-dire la zone où aucun rayon issu du Soleil ne parvient. Tracer également la zone de pénombre, où une partie des rayons du Soleil est masquée par la Lune, et de pleine lumière, où aucun rayon n'est masqué par la Lune.
Considérer chaque point du Soleil comme une source ponctuelle. Intéressez-vous surtout aux bords de celui-ci.
 Nature de la lumière
Nature de la lumière
Nous venons de voir que la lumière peut être vue parfois comme une onde, parfois comme une particule appelée photon.
 Le spectre électromagnétique
Le spectre électromagnétique
Les ondes radio, les microondes du four éponyme, la lumière, les UV nous donnant des coups de soleil, les rayons X pour photographier nos os brisés... sont tous des visages d'un même phénomène : l'onde électromagnétique.
Les longueurs d'onde de la lumière

Les différentes longueurs d'onde de la lumière, depuis les rayons gamma (courte longueur d'onde, grande énergie) jusqu'aux ondes radio (grande longueur d'onde, énergie faible). On notera que la lumière visible ne représente qu'une très faible portion de ce spectre.
Crédit :
ASM/Alain Hui-Bon-Hoa et Gilles Bessou
 L'approximation de l'optique géométrique
L'approximation de l'optique géométrique
Lorsque les grandeurs caractéristiques d'un système optique sont grandes devant la longueur d'onde, on peut négliger le phénomène de diffraction. On abandonne ainsi la description ondulatoire de la lumière, et on peut utiliser la notion de rayon lumineux. C'est le cadre de l'optique géométrique.
 Le rayon lumineux
Le rayon lumineux
Dans un milieu transparent, homogène et isotrope, la lumière se propage en ligne droite.
 Indice optique
Indice optique
Enfin, nous avons vu la définition de l'indice optique d'un MHTI. Il s'agit du rapport de la vitesse de la lumière dans le vide par celle dans ce milieu.
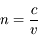
C'est une quantité supérieure à 1, dépendant du MHTI et de la longueur d'onde.
 Dans ce chapitre...
Dans ce chapitre...


 Hz pour sa partie visible, se propageant à la vitesse
Hz pour sa partie visible, se propageant à la vitesse 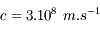 .
.
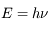 , où
, où 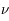 est la fréquence de l'onde électromagnétique précédemment introduite, et
est la fréquence de l'onde électromagnétique précédemment introduite, et 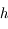 une constante, qui portera le nom du physicien Planck. Dans cet article, il parviendra à expliquer l'un des phénomènes encore mystérieux, l'effet photoélectrique. Il est d'ailleurs amusant de rappeler que c'est pour cet article que le père de la relativité recevra le prix Nobel. Le second phénomène, l'émission du
une constante, qui portera le nom du physicien Planck. Dans cet article, il parviendra à expliquer l'un des phénomènes encore mystérieux, l'effet photoélectrique. Il est d'ailleurs amusant de rappeler que c'est pour cet article que le père de la relativité recevra le prix Nobel. Le second phénomène, l'émission du 




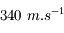 à température ambiante et à pression atmosphérique), ou dans les autres milieux (eau, solides...).
à température ambiante et à pression atmosphérique), ou dans les autres milieux (eau, solides...).


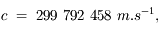
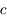 . De cette constatation naîtra la théorie de la relativité restreinte.
. De cette constatation naîtra la théorie de la relativité restreinte.
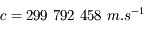 .
.
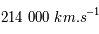 (avec une erreur de l'ordre de 30 % par rapport à la valeur mesurée aujourd'hui).
(avec une erreur de l'ordre de 30 % par rapport à la valeur mesurée aujourd'hui).
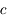 .
.


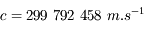 , et ce, dans n'importe quel référentiel.
, et ce, dans n'importe quel référentiel.


 ). Dans le cas des vagues, elle est de l'ordre d'une seconde. Inversement, on voit passer une vague par seconde environ. Un peu plus si le temps entre deux vagues est plus court, un peu moins, s'il est plus long. C'est ce qu'on appelle la fréquence (notée
). Dans le cas des vagues, elle est de l'ordre d'une seconde. Inversement, on voit passer une vague par seconde environ. Un peu plus si le temps entre deux vagues est plus court, un peu moins, s'il est plus long. C'est ce qu'on appelle la fréquence (notée 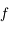 ou
ou 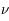 ). Elle est définit comme l'inverse de la période temporelle.
). Elle est définit comme l'inverse de la période temporelle.
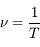
 .
.
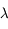 . Elle s'exprime en mètre.
. Elle s'exprime en mètre.

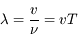
 fixée, si la vitesse augmente, la longueur d'onde augmente. Les vagues fuient plus vite et donc la distance entre elles grandit.
fixée, si la vitesse augmente, la longueur d'onde augmente. Les vagues fuient plus vite et donc la distance entre elles grandit.
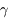 qui seront générés.
qui seront générés.
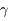 en passant par le visible. Pourtant, ce sont tous la manifestation d'un même phénomène, la propagation d'une onde électromagnétique. Seule la fréquence varie.
en passant par le visible. Pourtant, ce sont tous la manifestation d'un même phénomène, la propagation d'une onde électromagnétique. Seule la fréquence varie.
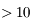
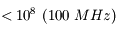
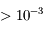
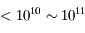
 )...
)...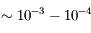
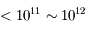
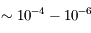
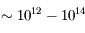
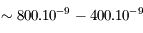
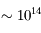
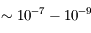
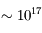
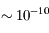
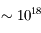
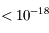
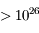



 du milieu comme étant le rapport de la vitesse de la lumière dans le vide sur sa vitesse
du milieu comme étant le rapport de la vitesse de la lumière dans le vide sur sa vitesse 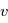 dans le milieu.
dans le milieu.
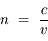
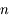 est toujours supérieur à 1.
est toujours supérieur à 1.

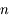 est toujours supérieur à 1.
est toujours supérieur à 1.
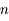 dépend de la longueur d'onde.
dépend de la longueur d'onde.
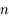 .
.
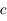 partout, tout le temps. Or, on constate qu'elle va moins vite dans les MHTI. En fait, dans ce type de milieu, la lumière interagit avec les molécules composant celui-ci. Entre chaque molécule, les photons voyagent à
partout, tout le temps. Or, on constate qu'elle va moins vite dans les MHTI. En fait, dans ce type de milieu, la lumière interagit avec les molécules composant celui-ci. Entre chaque molécule, les photons voyagent à 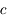 . Mais en interagissant, ils sont absorbés puis réémis, ils changent plusieurs fois de directions... Vu de loin, tout se passe comme si la lumière allait moins vite.
. Mais en interagissant, ils sont absorbés puis réémis, ils changent plusieurs fois de directions... Vu de loin, tout se passe comme si la lumière allait moins vite.
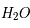 . Parfois, l'atome d'hydrogène est remplacé par son isotope stable, le deutérium. Ce dernier est composé d'un proton et d'un neutron. Il est deux fois plus lourd que l'hydrogène. Cette molécule
. Parfois, l'atome d'hydrogène est remplacé par son isotope stable, le deutérium. Ce dernier est composé d'un proton et d'un neutron. Il est deux fois plus lourd que l'hydrogène. Cette molécule 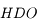 est alors appelée eau semi-lourde. L'eau lourde, quant à elle, est constituée de deux atomes de deutérium :
est alors appelée eau semi-lourde. L'eau lourde, quant à elle, est constituée de deux atomes de deutérium : 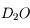 .
.
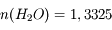 . Calculer la vitesse de la lumière dans cette eau.
. Calculer la vitesse de la lumière dans cette eau.
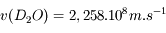 . Calculer son indice optique.
. Calculer son indice optique.

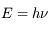
 est appelée constante de Planck, et vaut
est appelée constante de Planck, et vaut 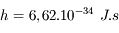 .
.



 ).
).

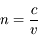
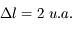 au cours du temps.
au cours du temps.
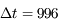 secondes, on peut en déduire la vitesse
secondes, on peut en déduire la vitesse 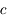 de la lumière :
de la lumière :
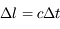
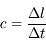
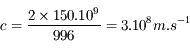
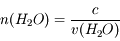
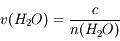
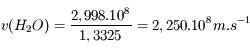
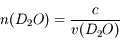
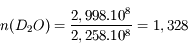
 . Les rayons passant à côté de la pièce ne sont pas stoppés, ceux la frappant si. On ne les retrouve pas de l'autre côté. Les rayons tangents à la pièce délimitent donc la zone d'ombre.
. Les rayons passant à côté de la pièce ne sont pas stoppés, ceux la frappant si. On ne les retrouve pas de l'autre côté. Les rayons tangents à la pièce délimitent donc la zone d'ombre.