Dès leur introduction, les caméras CCD ont très rapidement remplacé les plaques photographiques pour l'observation en astronomie. Plus sensibles, de réponse plus linéaire, fournissant un signal digitalisé, avec une réponse spectrale plus modulable, spatialisables... elles offrent des perspectives que la plaque photographique n'ouvrait pas.
Les propriétés élémentaires des caméras CCD sont tout d'abord décrites, en lien avec les propriétés générales des détecteurs déjà présentées, et reprenant essentiellement les propriétés des caméras CCD aujourd'hui.
Les dernières pages de cette section se concentrent sur diverses notions relatives aux observations, en détaillant diverses sources de bruit. Elles ont pour but la compréhension physique de certains phénomènes (et ne satisferont pas entièrement l'astronome amateur confronté à des problèmes bien pratiques).

L'amas de galaxies d'Hercule, vu par la caméra grand champ de l'observatoire CFH.
Crédit :
CFH
Récepteurs à transferts de charge (CCD)
Le détecteur CCD, pour l'anglais charge coupled device, assure la conversion d'un signal lumineux en un signal électrique. Cette technique introduite en 1969 est en usage en astronomie depuis la fin des années 70, fournissant des détecteurs pour les domaines visible, infrarouge et proche UV.
Le fonctionnement d'un détecteur CCD peut être ainsi résumé :
- Chaque pixel de la matrice CCD correspond à un élément semi-conducteur
en sandwich dans un condensateur électrique.
- Un photon incident crée un photo-électron, lorsqu'il apporte à un électron du matériau semi-conducteur l'énergie nécessaire pour franchir le seuil énergétique (gap).
- Les photo-électrons sont stockés dans le puits de potentiel qu'est le pixel convenablement polarisé.
- La lecture de ces photo-électrons est commandée par polarisation via des
transistors à effet de champ. Elle a lieu soit directement, un obturateur cachant la source, soit par transfert de trame. Dans ce dernier cas, une moitié de la surface du CCD est réservée à la collecte du signal; l'autre moitié n'est jamais éclairée, mais recueille les photo-électrons de la partie réceptrice, avant la lecture complète et le transfert des charges vers l'étage d'amplification.
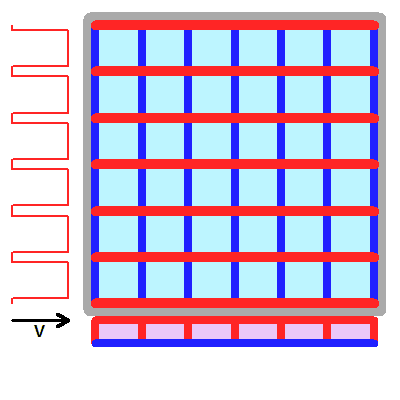
Les colonnes de la galette CCD sont définies en dur dans le silicium par des rangées dopées p (en bleu foncé) ; les lignes sont créés par une différence de potentiel (les zones de potentiel bas, en rouge, font fuir les électrons). Le registre de lecture (en violet) équivaut à une ligne de la galette.
Crédit :
ASM
Définition des pixels
Une caméra CCD comprend des lignes et des colonnes, définissant les pixels. Le principe de lecture d'une CCD conduit à définir les bornes des colonnes par un dopage p gravé dans le silicium. En revanche, les bornes des lignes sont définies par une polarisation commandée. Le puits de potentiel qu'est un pixel est statique dans la phase d'acquisition du signal scientifique, puis variable pendant la lecture des pixels.
Principe
Comment, dans un détecteur CCD, un photon éveille un photo-électron, et comment celui-ci devient signal.
Principe de détection 
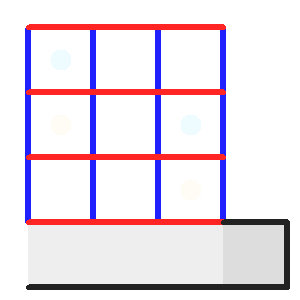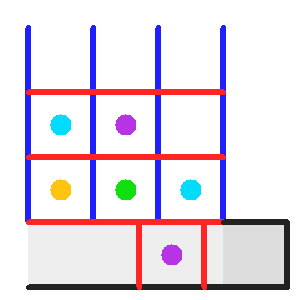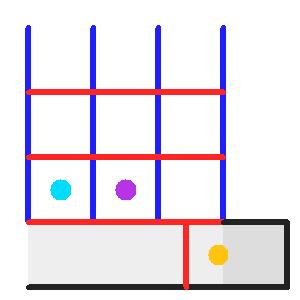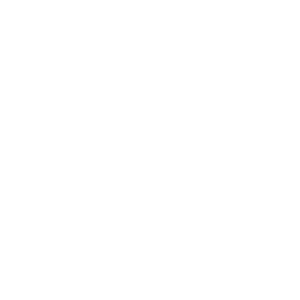
Processus d'acquisition : pose, transfert dans le registre et lecture du registre.
Crédit :
ASM
Processus de lecture
Les étapes de l'enregistrement et de la lecture d'une image CCD sont décrites dans l'animation ci-jointe :
- Durant la pose, les pixels se remplissent peu à peu en photo-électrons. .
- La variation du potentiel définissant les lignes du CCD conduit au transfert, ligne par ligne, vers le registre (grisé).
- Le registre transfère les photoélectrons vers la zone de lecture (gris foncé), pour charger un condensateur. La tension aux bornes du condensateur est ensuite amplifiée et numérisée.
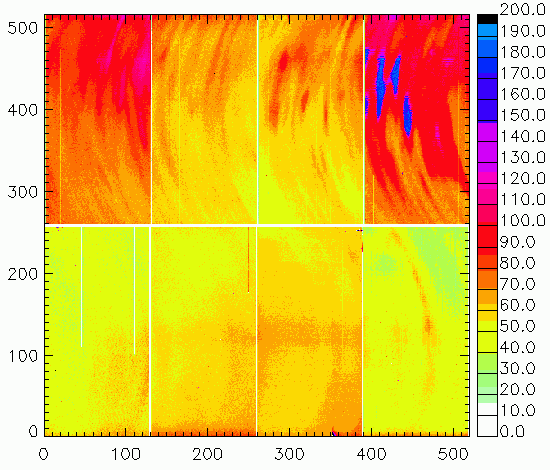
Signal d'obscurité de la caméra UH8k de l'observatoire CFH.
Crédit :
CFH
Propriétés
Le signal d'obscurité, enregistré alors qu'aucune source n'éclaire le détecteur, rend compte de divers signaux et bruits affectant toute image délivrée par une caméra CCD.
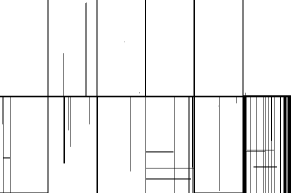
Colonnes mortes sur les CCD de la caméra CFH12k
Crédit :
CFHT

CCD : phénomène de traînée (smearing).
La lecture de l'image a lieu sans obturateur, par translation le long d'une colonne (ici, vers le haut). Au passage d'un pixel fortement illuminé, l'information des pixels en amont, dont la lecture passe par ce pixel illuminé, est altérée par la superposition de photo-électrons supplémentaires. La colonne blanche est une colonne morte.
Crédit :
CFHT

Franges d'interférence de la caméra : les photons, surtout dans le
rouge, peuvent être réfléchis dans la zone sensible du CCD avant
d'être absorbés. Ceci conduit à des franges d'interférence,
gênantes car elles modulent le champ de réponse de la caméra.
Crédit :
CFHT

Le phénomène de fringing se superpose au nuage L183 observé en bande I au CFHT.
Crédit :
CFHT
Quelques défauts
Divers artefacts dégradent la réponse idéale d'un CCD.
- Colonne morte : Un pixel défectueux pour la fonction de
lecture bloque l'information de toute une
colonne.
- Traînée : L'absence d'obturateur lors de la lecture
conduit à un phénomène de
traînée.
- Frange : Des franges
d'égale épaisseur apparaissent en lumière
monochromatique, et traduisent les irrégularités d'épaisseur de la
galette. Ne pas les corriger nuit aux
observations.
Les principales caractéristiques
- Rendement quantique :
Mesure le rapport du nombre de photo-électrons créés au nombre de photons incidents. Sa valeur est élevée : de 40 à 80% selon la technologie du CCD (CCD épais éclairé par l'avant, ou CCD aminci éclairé par l'arrière), là où la plaque photo était limitée au mieux à quelques %.
- Dynamique : Grande dynamique, et linéarité idéale, jusqu'à la saturation, lorsque le puits de potentiel est plein (typiquement de l'ordre de
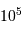 photo-électrons pour les caméras actuelles avec des pixels de côté de l'ordre de 10 micromètres).
photo-électrons pour les caméras actuelles avec des pixels de côté de l'ordre de 10 micromètres). - Bruit de fond : Faible (d'autant plus faible que la caméra est refroidie).
- Numérisation : Le signal est directement numérisé en sortie de l'étage d'amplification.
- Taille : Les tailles actuelles maximales pour l'observation astrophysique sont de l'ordre de 4k
 4k pixels, soit 16 millions de pixels; la taille est le seul domaine où la plaque photographique proposait de meilleures performances. Les pixels ont des côtés de typiquement 10 micromètres.
4k pixels, soit 16 millions de pixels; la taille est le seul domaine où la plaque photographique proposait de meilleures performances. Les pixels ont des côtés de typiquement 10 micromètres. - Domaine spectral : Le domaine spectral est fonction du matériau semi-conducteur (de 0.4 à 1.2 micromètres pour le silicium), mais aussi de
son éventuel dopant ; l'adjonction d'une couche de matériau aux propriétés photovoltaïques à un CCD permet d'étendre le domaine spectral de sensibilité.
Conversion analogique-numérique
Le signal numérisé est proportionnel au nombre de photo-électrons :
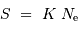
avec le facteur de conversion 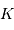 exprimé en ADU par électron.
exprimé en ADU par électron.
Le signal numérisé est codé sur un nombre de bits en accord avec la dynamique du signal.
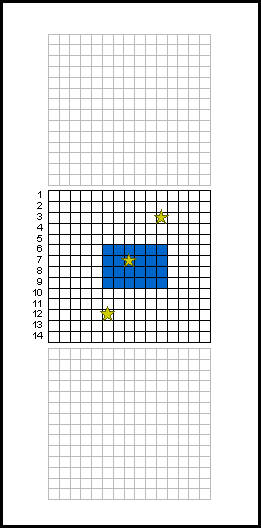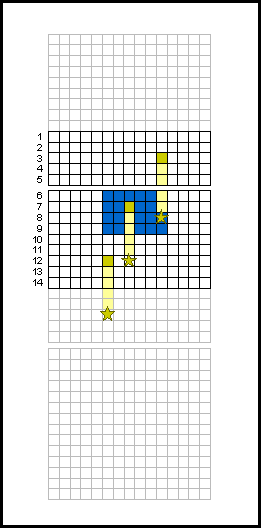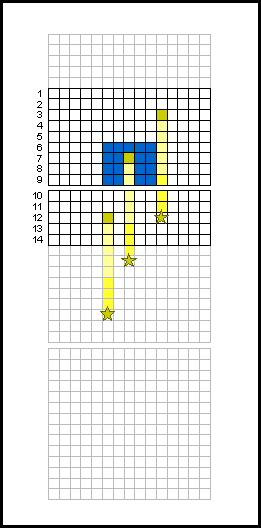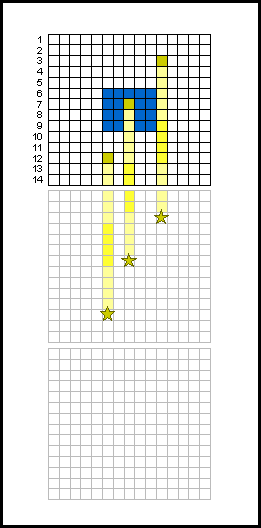
CCD : phénomène de traînée lors du transfert de trame.
Crédit :
COROT
Transfert de trame
Pour une caméra sans obturateur, le phénomène de traînée est la signature de la lecture des images par transfert de trame.
Exemple de caractéristiques
Les caractéristiques des 12 CCD d'une caméra à grand champ du télescope CFH sont présentées par l'appliquette ci-dessous.
L'unité ADU signifie analog to digital unit (et kADU = 1000 ADU) ;
RN = read-out noise = bruit de lecture ; lin = domaine de linéarité.
Le rendement quantique, exprimé en pourcentage, est donnée pour les bandes B, V, R, I et Z'.

Bruit de transfert
L'enregistrement d'une image du courant d'obscurité comporte nécessairement les
bruits d'obscurité et de transfert. Le transfert est responsable du gradient de signal sur cette image de courant d'obscurité.
Courant d'obscurité
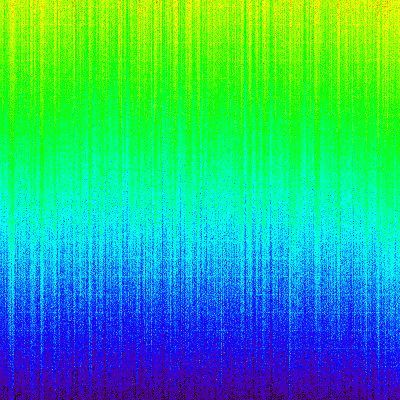
Image de courant d'obscurité. Le gradient sur l'image est dû au gradient de bruit de transfert le long des colonnes.
Crédit :
ASM
Champ plat
Le champ plat rend compte du caractère non uniforme du signal collecté en réponse à une source uniforme.
Champ plat
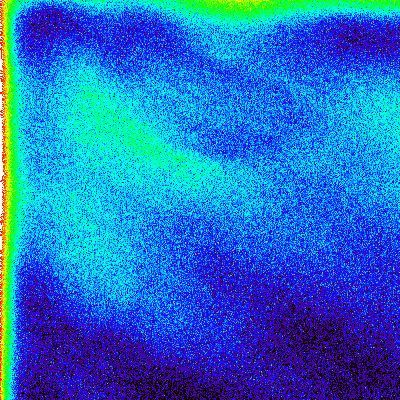
Image de champ plat. Les conditions d'éclairement non uniformes sont responsables entre autres des fortes variations sur les bords gauche et supérieur.
Crédit :
ASM
 Objectifs
Objectifs
Examiner les étapes générant les bruits les plus importants pour une image enregistrée. L'agitation thermique du capteur et le transfert des électrons vers les registres de lecture comptent parmi les étapes les plus bruyantes d'une séquence d'observation.
Etapes de lecture
Après la phase d'acquisition du signal scientifique, l'horloge qui pilote l'électronique du CCD commande le transfert des photoélectrons collectés dans les pixels vers un registre de lecture. Le registre, de taille égale à une ligne du CCD, est lui-même lu séquentiellement.
Le déplacement des électrons, qui se vident d'un pixel dans un autre, est provoqué par une bascule des tensions de polarisation du CCD.
Pour chacun des pixels lus, les électrons vont charger un condensateur ; la tension aux bornes du condensateur, proportionnelle à la charge collectée, est ensuite amplifiée analogiquement, puis convertie en un signal numérique.
Courant et bruit d'obscurité
Le courant d'obscurité est associé à la création de charges par agitation thermique, sans intervention de quelque signal lumineux. Le nombre de charges créées dépend fortement de la température : typiquement en moyenne 0.1 électron par pixel par seconde.
Le courant d'obscurité est un signal parasite. Comme il s'agit d'un processus poissonnien, ce signal est bruité : le bruit du processus varie comme la racine carrée du nombre de charges créées.
Bruit du transfert des charges
Les charges accumulées dans un pixel doivent transiter le long d'une colonne vers un registre, avant d'être amplifiées. L'efficacité de ce processus, quoique très bonne, n'est pas idéale. Le nombre de charges créées ainsi dépend du nombre 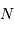 d'électrons par pixel à transférer, de l'inefficacité
d'électrons par pixel à transférer, de l'inefficacité 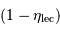 d'un transfert et du nombre total
d'un transfert et du nombre total 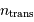 de transferts. Le bruit dû aux imperfections du transfert se monte à :
de transferts. Le bruit dû aux imperfections du transfert se monte à :
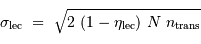
Le facteur 2 provient du fait que 2 pixels sont affectés : celui qui a perdu un électron, et celui qui l'a malencontreusement gagné.
Avec p.ex. un signal à hauteur de la moitié du puits quantique d'un pixel, de l'ordre de 50000 e-, une efficacité de transfert typiquement de 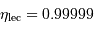 , et donc une inefficacité de
, et donc une inefficacité de 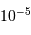 , et un millier de transferts en moyenne pour une colonne de 2k pixels, le bruit lié au transfert est de 32 e-/pixel.
, et un millier de transferts en moyenne pour une colonne de 2k pixels, le bruit lié au transfert est de 32 e-/pixel.
Amplification, quantification
Le processus d'amplification du signal, qui permet aux circuits électroniques de travailler avec de plus forts signaux, est également peu bruité. On peut le négliger dans la grande majorité des cas devant les autres sources de bruit.
La conversion du signal analogique vers un codage numérique est menée avec un gain tel que le bruit de numérisation (lié à la nature quantique du codage) soit également négligeable. Ce gain vaut typiquement quelques électrons par
ADU (analog to digital unit).
Bruit de lecture
La lecture de la caméra va être entachée des bruits du courant d'obscurité, du transfert de charge et d'amplification. Selon les conditions, l'un ou l'autre des bruits domine :
- Si le détecteur n'est pas refroidi, le courant d'obscurité et donc son bruit est important.
- Le bruit de transfert est d'autant plus élevé que la fréquence de lecture est rapide.
 Caractéristiques d'une caméra CCD
Caractéristiques d'une caméra CCD
Difficulté : ☆
Temps : 15 min
On s'intéresse à quelques caractéristiques d'une caméra CCD KAF-0400.
Un pixel présente une capacité de charges de 80000 électrons.
La numérisation se fait sur 14 bits. Le bruit de lecture annoncé vaut 13 électrons.
Question 1)
Déterminer le rapport signal à bruit maximal par pixel.
Identifier le signal maximal, le bruit minimal.
Question 2)
Déterminer le gain 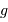 de la conversion ADU.
de la conversion ADU.
Déterminer l'entier maximal qui peut être codé sur 14 bits.
Question 3)
On montre que le bruit de quantification vaut 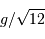 . Montrer qu'il est effectivement négligeable.
. Montrer qu'il est effectivement négligeable.
Il s'agit simplement d'une application numérique !
Champ plat
Le champ plat mesure la réponse du CCD d'une chaîne instrumentale à un éclairement uniforme. Cette réponse, idéalement uniforme, ne l'est bien sûr pas tout à fait dans la pratique. Les différences à une réponse uniforme proviennent du champ de variations de la réponse des pixels, des défauts de la galette CCD, et aussi des conditions d'éclairement qui peuvent être modulées par le montage instrumental en amont du détecteur.
Enregistrement du champ plat d'une matrice. Il est nécessaire de bien mesurer la réponse de la matrice CCD sur une source uniforme, afin d'identifier les gradients de réponse des pixels.
Crédit :
ASM
Détermination du champ plat
Obtenir un champ plat n'est pas toujours facile, car il faut disposer d'une source la plus uniforme possible. Différentes techniques permettent d'aboutir à un résultat performant :
- Observer un écran sur le dôme, éclairé par de multiples sources.
- Observer le ciel à l'aube ou au crépuscule.
- Calculer l'image médiane d'un très grand nombre de poses nocturnes.

La zone peinte en blanc sur le dôme peut servir à l'enregistrement de champ plat.
Crédit :
ASM
Signal d'obscurité
Comme son nom l'indique, le signal d'obscurité correspond au signal enregistré alors qu'aucune source n'éclaire le détecteur. Il correspond à la création de porteur de charges (typiquement 1 électron par pixel toutes les 10 secondes) par simple agitation thermique.
Obtenir une bonne image du courant d'obscurité nécessite de poser aussi longtemps que pour la pose scientifique. Ceci peut prendre du temps... mais n'a heureusement pas besoin d'être mené sur le ciel.
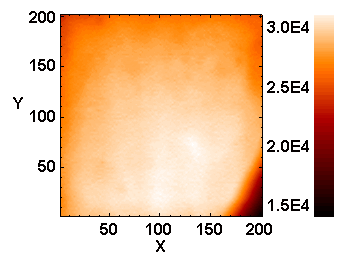
Le courant d'obscurité est modulé sur le champ de la caméra selon la technologie de fabrication des détecteurs. Des pixels abimés peuvent produire un grand nombre de charges parasites : on parle de pixels chauds.
Signal d'obscurité.
Crédit :
ASM
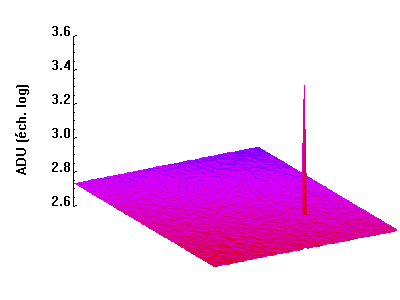
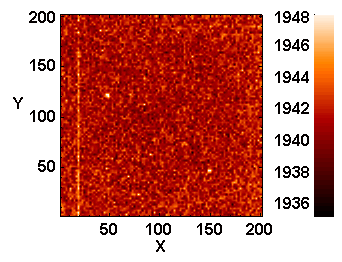
Le pixel chaud présente un très fort signal sur cette image de signal d'obscurité. Le signal numérique a été représenté en échelle logarithmique pour améliorer la dynamique de la représentation.
Crédit :
ASM
Traitement d'image
Les corrections d'obscurité et de champ plat redressent l'information photométrique d'une image.
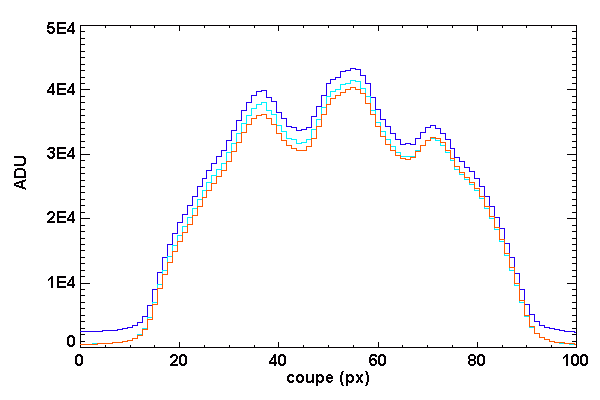
Coupe le long de 3 images de Jupiter observé dans le visible.
En bleu foncé sans correction du signal d'obscurité : on remarque que le fond de ciel n'est pas à zéro. En bleu ciel, après correction du signal d'obscurité : le signal du fond de ciel est ramené à valeur nulle. En rouge : après correction du champ plat.
Crédit :
ASM
 Objectifs
Objectifs
Deux étapes sont indispensables dans le traitement d'une image CCD. La correction d'un offset lié à divers signaux parasites dont le courant d'obscurité, et la correction de champ plat.
Le courant d'obscurité
Au signal astrophysique 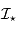 se superposent différentes contributions, additives, dont principalement le courant d'obscurité.
se superposent différentes contributions, additives, dont principalement le courant d'obscurité.
En raison du bruit thermique, le détecteur délivre un courant en l'absence de toute puissance lumineuse, appelé courant d'obscurité. Sa contribution 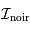 , additive, est à retrancher.
, additive, est à retrancher.
Carte de réponse
La réponse de la chaîne instrumentale, y compris la caméra, n'est pas uniforme.
Une pose sur une source uniforme fournit le champ plat : la réponse normalement uniforme à une excitation uniforme, en fait potentiellement déformée par les divers éléments, et modulée par la réponse non uniforme des pixels.
On note 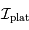 la réponse à cette excitation uniforme. Cet effet est multiplicatif.
la réponse à cette excitation uniforme. Cet effet est multiplicatif.
Séquence de traitement
On passe de l'image brute 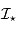 à l'image finale
à l'image finale 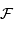 par soustraction des effets additifs et division par les effets multiplicatifs :
par soustraction des effets additifs et division par les effets multiplicatifs :
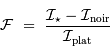
Idéalement, la réponse du champ plat est normalisée, de moyenne 1. En pratique, il est indispensable d'acquérir une image de champ plat avec le meilleur rapport signal à bruit. De toutes façons, l'étalonnage de la réponse 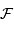 nécessite des sources de référence.
nécessite des sources de référence.
Correction élémentaire du champ plat
A l'aide de l'appliquette ci-jointe, assurer la correction du champ plat.
Correction du champ plat 
- Sélectionner la 1ère image. Si besoin, adapter l'échelle de couleur avec la touche auto.
- Sélection l'opération coupe, puis une ligne de coupe évitant les objets les plus brillants.
- Sélection l'opération division, puis la 1ère image et l'image de champ plat, et nommer l'image corrigée.
- Réaliser sur cette nouvelle image la coupe précédente. Comparer.
Correction élémentaire du courant d'obscurité
A l'aide de l'appliquette ci-jointe, assurer la correction du courant d'obscurité. La correspondance entre les noms de fichiers et les images est la suivante, selon le rang des lettres :
- f = flat : champ plat, j : image jovienne, d=dark : courant d'obscurité.
- s : SYMPA : projet de sismologie jovienne ; images enregistrées en 2004 au télescope de l'Observatoire San Pedro Martir au Mexique.
- A ou B : 2 familles d'images enregistrées par 2 voies différentes de l'instrument SYMPA.
- N : numéro de l'image jovienne.
Correction du courant d'obscurité 
- Procéder comme à l'appliquette précédente.
- Vérifier l'importance d'associer les bons fichiers (familles A ou B).
Rapport signal à bruit du signal d'obscurité
Le signal d'obscurité doit être enregistré avec un rapport signal à bruit meilleur que celui des images à traiter.
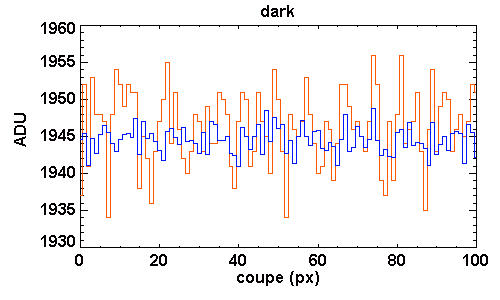
Coupe le long de 2 images d'obscurité, l'une élémentaire, l'autre résultant de la moyenne de 20 images élémentaires. L'amélioration du rapport
signal à bruit est bénéfique pour le traitement des images à suivre.
Crédit :
ASM
 Objectifs
Objectifs
Les étapes de correction des signaux de courant d'obscurité et de champ plat ne se font pas sans bruit. Le but de cette page est d'estimer les performances de ces opérations, et de montrer que les signaux de courant d'obscurité et de champ plat doivent être connus avec un rapport signal à bruit (bien) meilleur que celui du signal seul.
Courant d'obscurité
La correction consiste à soustraire au signal le signal d'obscurité. Ce dernier est acquis lors d'une pose longue, sans source. Cette soustraction s'exprime par :
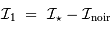
Les bruits des signaux d'entrée sont respectivement 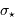 et
et 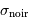 (le bruit de la source comprend le bruit de photons). Non corrélés, il s'additionnent quadratiquement pour donner le bruit de la différence :
(le bruit de la source comprend le bruit de photons). Non corrélés, il s'additionnent quadratiquement pour donner le bruit de la différence :
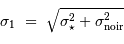
Le rapport signal à bruit s'écrit donc :
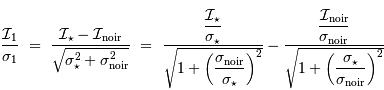
Ceci montre que le rapport signal à bruit après correction du courant d'obscurité est moindre qu'avant correction :
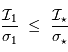
Cette correction reste néanmoins nécessaire pour corriger certains effets structurels de la caméra.
Le cas 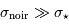 où le bruit de courant d'obscurité domine apparaît très inintéressant : la performance de la correction sera d'autant bruitée. En revanche, si le signal d'obscurité est bien moins bruité que le signal astrophysique, càd
où le bruit de courant d'obscurité domine apparaît très inintéressant : la performance de la correction sera d'autant bruitée. En revanche, si le signal d'obscurité est bien moins bruité que le signal astrophysique, càd
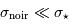 , on récupère :
, on récupère :
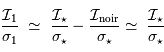
Le rapport signal à bruit est très peu dégradé. Il est donc indispensable d'acquérir une bonne image très peu bruitée du courant d'obscurité.
Champ plat
La correction de champ plat consiste à diviser le signal 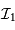 par le signal de champ plat normalisé (et éventuellement corrigé du courant d'obscurité). Le champ plat est acquis lors d'une pose sur une source la plus uniforme possible.
La division s'exprime :
par le signal de champ plat normalisé (et éventuellement corrigé du courant d'obscurité). Le champ plat est acquis lors d'une pose sur une source la plus uniforme possible.
La division s'exprime :
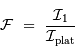
Les bruits en entrée sont respectivement 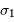 et
et 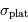 . Le bruit final dépend des bruits et signaux initiaux via :
. Le bruit final dépend des bruits et signaux initiaux via :
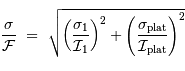
Pour s'en convaincre, il suffit de différencier logarithmiquement la relation définissant 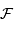 . On peut donc réécrire le rapport signal à bruit :
. On peut donc réécrire le rapport signal à bruit :
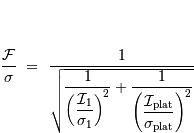
On remarque que cette correction dégrade nécessairement le rapport signal à bruit, car de toutes façons :
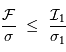
Il est inintéressant d'avoir un champ plat très bruité, car la performance sera limitée au rapport signal à bruit du champ plat dans ce cas. En revanche, si le champ plat est peu bruité 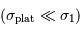 , on obtient :
, on obtient :
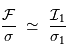
Il est donc indispensable d'acquérir une image de champ plat la moins bruitée possible. Ceci peut nécessiter une longue durée d'observation sur une source artificielle uniforme.
Enfin, on remarque dans cette opération qu'un signal bruité est moins dégradé qu'un signal peu bruité. En effet, corriger un signal peu bruité nécessite une correction de qualité meilleure encore.
Corrections
A l'aide de l'appliquette ci-jointe, assurer la correction du signal d'obscurité sur les images de Jupiter. La correspondance entre les noms de fichiers et les images est la suivante, selon le rang des lettres :
- f=flat : champ plat, j : image jovienne, d=dark : courant d'obscurité.
- s : SYMPA : projet de sismologie jovienne ; images enregistrées en 2004 au télescope de l'Observatoire San Pedro Martir au Mexique.
- e : image élémentaire ; s = image sommée
- N : numéro de l'image (facultatif)
Correction de l'image Jovienne 
Réaliser les opérations de corrections du courant d'obscurité et
du champ plat, et comparer les résultats par des coupes d'images.
Voir le mode d'emploi de l'appliquette donné
précédemment.
Rapport signal à bruit de différentes sources
Le tableau de l'appliquette ci-jointe donne les signaux moyens, par pixel, du courant d'obscurité (dark) et du champ plat (flat), ainsi que de diverses sources plus ou moins brillantes. On cherche à déterminer le rapport signal à bruit des observations. Le bruit de lecture est estimé à 20 e-.

- La 1ère étape consiste à tenir compte du bruit de lecture (pour lequel on n'a pas de signal spécifique, contrairement aux signaux d'obscurité et de champ plat). Calculer dans la colonne Be la contribution des bruits stellaires et de lecture.
- En déduire le rapport signal à bruit SNRe des sources avant toute correction.
- Déterminer le signal Ii corrigé du courant d'obscurité.
- Déterminer le bruit Bi tenant compte du signal lu et du courant d'obscurité.
- En déduire le rapport signal à bruit SNRi
- Déterminer le signal I corrigé du champ plat.
- Que vaut le rapport signal à bruit du signal de champ plat ? Le calculer indépendamment du tableau.
- En déduire le rapport signal à bruit final SNR, fonction du rapport signal à bruit SNRi et de celui de champ plat (les inverses des carrés des rapports s'additionnent pour cette correction).
En fonction de ce qui précède, comparer l'évolution des rapports signaux à bruits des diverses sources.
- Quelle étape est la plus bruyante, en fonction de la luminosité de la source ?
- Quels types de sources sont les mieux corrigés ?
T'as de beaux yeux, tu sais
L'oeil humain est un instrument très évolué : focale variable, diaphragme ajustable, vision stéréoscopique pour la perception du relief et des distances, transmission correcte dans le visible....
Quelques éléments de l'instrument oeil : diaphragme d'ouverture, monture, protection amovible...
Crédit :
ASM
Réponse spectrale de l'oeil
La courbe de réponse spectrale de l'oeil humain est centrée sur le maximum du spectre solaire, et décroît très rapidement vers le bleu et le rouge.
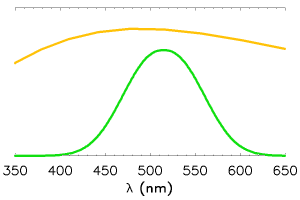
Spectre solaire perçu au travers de l'atmosphère (en orange) et courbe de sensibilité spectrale typique de l'oeil humain (en vert). La correspondance des maxima n'est certes pas un hasard, mais le fruit de l'évolution.
Crédit :
ASM
L'oeil
L'oeil est un instrument très perfectionné, mais malheureusement non adapté à l'observation d'objets très lointains, et donc de petite taille angulaire et de luminosité réduite.
Résolution angulaire
Ouverte au maximum, après de longues minutes d'adaptation au noir le plus complet, la pupille atteint un diamètre maximal de l'ordre de 6 mm. La tache de diffraction qui en résulte ne permet pas de résoudre, en lumière jaune, des détails angulaires plus fins que
20".
Résolution temporelle
L'oeil humain construit de l'ordre de 20 images par seconde. Cette cadence n'est pas "réglable" : impossible de poser pour scruter un objet fixe mais faiblement lumineux, comme le fait une plaque photo ou tout autre détecteur.
Résolution spectrale
L'oeil peut distinguer un très grand nombre de couleurs, dans un domaine spectral de 400 à 700 nm principalement. Mais l'impression des couleurs reste toute relative, et dépend de nombreux paramètres, parmi lesquels l'intensité lumineuse.
La réponse de l'oeil humain dans le bleu évolue très fortement, et très défavorablement, avec l'age.
- Question 1
Aide :
Identifier le signal maximal, le bruit minimal.
Solution :
Le rapport maximal est fixé par le signal maximal, 80000, et le bruit minimal. Les 13 électrons de lecture sont négligeables devant le bruit de photoélectrons.
Il vaut donc environ 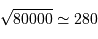 .
.
- Question 2
Aide :
Déterminer l'entier maximal qui peut être codé sur 14 bits.
Solution :
Un signal numérisé sur 14 bits est limité à 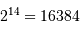 .
Le gain vaut 80000 / 16384 = 4.9 électrons/ADU.
.
Le gain vaut 80000 / 16384 = 4.9 électrons/ADU.
- Question 3
Aide :
Il s'agit simplement d'une application numérique !
Solution :
Le bruit de quantification vaut 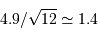 électrons. Il est effectivement négligeable.
électrons. Il est effectivement négligeable.
- Question 4
Aide :
Le bruit en entrée de l'amplificateur vaut le bruit en sortie divisé par le gain 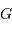 de l'amplificateur.
de l'amplificateur.
Solution :
Le bruit en sortie vaut, par application de la définition intégrale et avec les hypothèses simplificatrices :
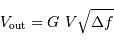
Le bruit en entrée vaut donc :
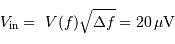
Traduit en électron, cela donne, avec un facteur de conversion
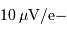 , 2 électrons.
, 2 électrons.
Ce bruit est négligeable devant le bruit de lecture.









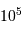 photo-électrons pour les caméras actuelles avec des pixels de côté de l'ordre de 10 micromètres).
photo-électrons pour les caméras actuelles avec des pixels de côté de l'ordre de 10 micromètres).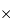 4k pixels, soit 16 millions de pixels; la taille est le seul domaine où la plaque photographique proposait de meilleures performances. Les pixels ont des côtés de typiquement 10 micromètres.
4k pixels, soit 16 millions de pixels; la taille est le seul domaine où la plaque photographique proposait de meilleures performances. Les pixels ont des côtés de typiquement 10 micromètres.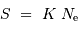
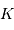 exprimé en ADU par électron.
exprimé en ADU par électron.



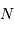 d'électrons par pixel à transférer, de l'inefficacité
d'électrons par pixel à transférer, de l'inefficacité 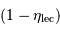 d'un transfert et du nombre total
d'un transfert et du nombre total 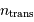 de transferts. Le bruit dû aux imperfections du transfert se monte à :
de transferts. Le bruit dû aux imperfections du transfert se monte à :
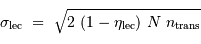
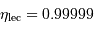 , et donc une inefficacité de
, et donc une inefficacité de 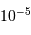 , et un millier de transferts en moyenne pour une colonne de 2k pixels, le bruit lié au transfert est de 32 e-/pixel.
, et un millier de transferts en moyenne pour une colonne de 2k pixels, le bruit lié au transfert est de 32 e-/pixel.
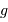 de la conversion ADU.
de la conversion ADU.
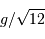 . Montrer qu'il est effectivement négligeable.
. Montrer qu'il est effectivement négligeable.
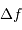 :
:
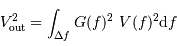
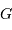 est constant sur la bande passante, et que le bruit
est constant sur la bande passante, et que le bruit 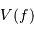 est blanc, avec
est blanc, avec 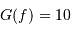 ,
, 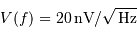 et
et 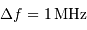 .
Calculer le bruit en sortie d'amplificateur, en déduire le bruit équivalent en entrée d'amplificateur, puis l'exprimer en nombre d'électrons, sachant que le facteur de conversion de l'étage de sortie du CCD vaut
.
Calculer le bruit en sortie d'amplificateur, en déduire le bruit équivalent en entrée d'amplificateur, puis l'exprimer en nombre d'électrons, sachant que le facteur de conversion de l'étage de sortie du CCD vaut 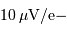 . Conclure.
. Conclure.
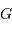 de l'amplificateur.
de l'amplificateur.




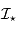 se superposent différentes contributions, additives, dont principalement le courant d'obscurité.
se superposent différentes contributions, additives, dont principalement le courant d'obscurité.
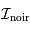 , additive, est à retrancher.
, additive, est à retrancher.
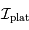 la réponse à cette excitation uniforme. Cet effet est multiplicatif.
la réponse à cette excitation uniforme. Cet effet est multiplicatif.
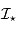 à l'image finale
à l'image finale 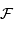 par soustraction des effets additifs et division par les effets multiplicatifs :
par soustraction des effets additifs et division par les effets multiplicatifs :
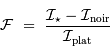
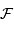 nécessite des sources de référence.
nécessite des sources de référence.

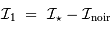
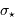 et
et 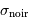 (le bruit de la source comprend le
(le bruit de la source comprend le 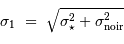
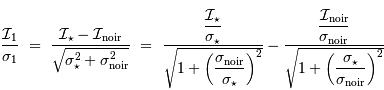
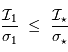
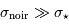 où le bruit de courant d'obscurité domine apparaît très inintéressant : la performance de la correction sera d'autant bruitée. En revanche, si le signal d'obscurité est bien moins bruité que le signal astrophysique, càd
où le bruit de courant d'obscurité domine apparaît très inintéressant : la performance de la correction sera d'autant bruitée. En revanche, si le signal d'obscurité est bien moins bruité que le signal astrophysique, càd
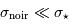 , on récupère :
, on récupère :
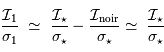
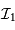 par le signal de champ plat normalisé (et éventuellement corrigé du courant d'obscurité). Le champ plat est acquis lors d'une pose sur une source la plus uniforme possible.
La division s'exprime :
par le signal de champ plat normalisé (et éventuellement corrigé du courant d'obscurité). Le champ plat est acquis lors d'une pose sur une source la plus uniforme possible.
La division s'exprime :
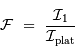
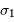 et
et 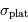 . Le bruit final dépend des bruits et signaux initiaux via :
. Le bruit final dépend des bruits et signaux initiaux via :
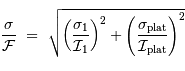
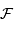 . On peut donc réécrire le rapport signal à bruit :
. On peut donc réécrire le rapport signal à bruit :
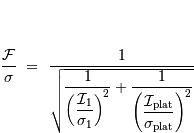
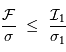
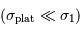 , on obtient :
, on obtient :
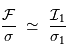


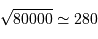 .
.
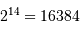 .
Le gain vaut 80000 / 16384 = 4.9 électrons/ADU.
.
Le gain vaut 80000 / 16384 = 4.9 électrons/ADU.
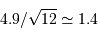 électrons. Il est effectivement négligeable.
électrons. Il est effectivement négligeable.
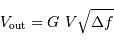
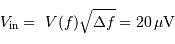
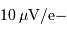 , 2 électrons.
, 2 électrons.