Collecter le signal, c'est assurer que les photons arrivent nombreux et en bon ordre aux différents foyers d'un télescope. Qualités optique et mécanique se conjuguent pour accomplir cette tâche.
Le miroir primaire est le ... premier miroir vu par les photons. Il présente généralement un profil parabolique. Le deuxième, s'il y en a un, est appelé ... secondaire.
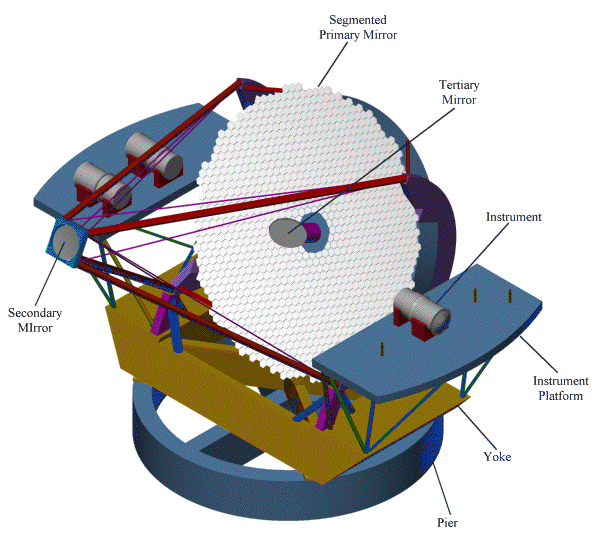
Les 2 télescopes Keck, plus grands collecteurs dans le visible depuis le début des années 1990, ont des miroirs segmentés (càd en plusieurs morceaux), et illuminent les foyers Cassegrain et Nasmyth. Ce dernier, après passage du faisceau sur l'axe en altitude, est découplé du télescope.
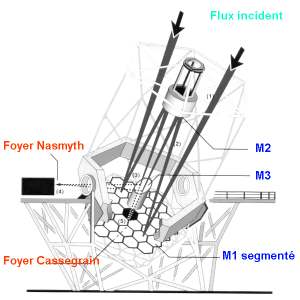
Une configuration classique est la combinaison de 2 miroirs, l'un parabolique, l'autre hyperbolique convexe, dans la configuration Cassegrain. Les miroirs ne sont plus nécessairement monoblocs ; c'est le cas du télescope optique le plus grand en service actuellement, le télescope Keck.
Dans le domaine radio, il est nécessaire d'avoir une antenne de grande taille :
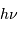par photon est très faible dans le domaine radio.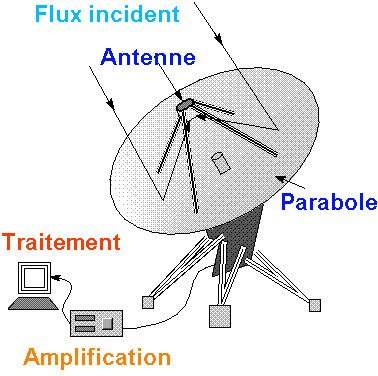
Le domaine des courtes longueurs d'onde présente de nombreuses particularités. Entre autres :
.
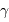PrérequisOptique géométrique. Formation d'image au foyer primaire d'un télescope.
ObjectifsQuelques notions sur les collecteurs de photons en astronomie.
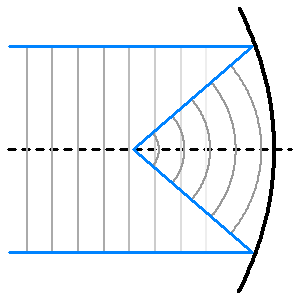
Le signal d'un objet très lointain, non résolu spatialement, est une onde plane. Observer cette onde plane, c'est la focaliser en un point. Une surface mathématique sait faire cette opération : le paraboloïde de révolution (révolution d'une parabole autour de son axe).
Mathématiquement, la parabole conjugue l'infini à un point ; optiquement, elle permet de transformer une onde plane en onde sphérique. Ceci n'est rigoureusement vrai que pour un rayon parallèle à l'axe optique. L'aberration de sphéricité apparaît pour les rayons inclinés sur l'axe.
Les lois de l'optique permettent de caractériser les qualités de la collecte.
Les collecteurs de photons s'appuient sur de multiples configurations optiques. On note principalement :
PrérequisOptique géométrique. Formation d'image au foyer primaire d'un télescope. Montures des télescopes.
ObjectifsAperçu des diverses configurations optiques pour un télescope.
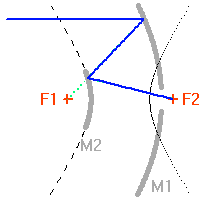
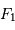, transformant une onde plane en onde sphérique. L'hyperbole échange les 2 foyers 
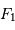et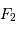 
: l'onde sphérique converge alors en 
.
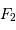Plusieurs configurations optiques permettent de réaliser pratiquement la convergence d'une onde plane en un foyer. Selon l'usage, astronomie amateur ou professionnelle, elles diffèrent, par leur performances et leurs coûts.
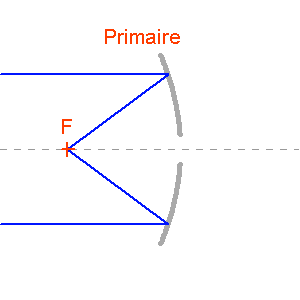
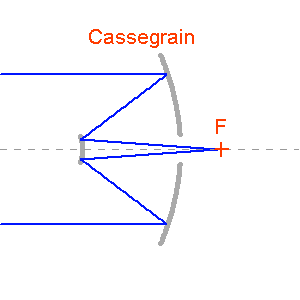
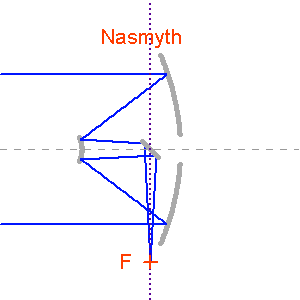
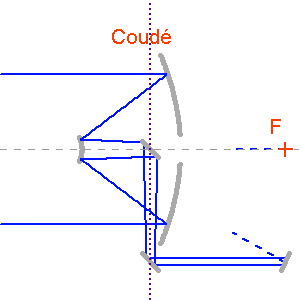
Un télescope professionnel, usuellement de type Cassegrain ou Ritchey-Chrétien, présentera plusieurs combinaison de foyers.
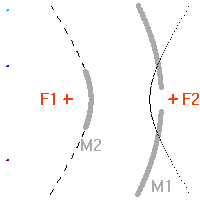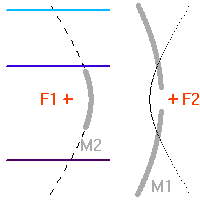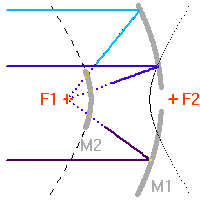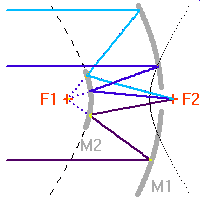
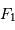, transformant une onde plane en onde sphérique. L'hyperbole échange les 2 foyers 
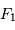et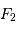 
: l'onde sphérique converge alors en 
.
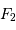La transformation d'une onde plane en onde sphérique, puis de l'onde sphérique en une autre onde sphérique convergeant au foyer du télescope, est une application directe des propriétés des coniques.
VLT 
Pour un télescope en monture azimutale, telles les 4 unités du VLT, plusieurs trains optiques permettent d'illuminer les différents foyers : Cassegrain, Nasmyth, coudé.
L'appliquette ci-dessous décompose différents éléments d'une des unités du VLT.
Focale équivalenteDifficulté : ☆ Temps : 15 min
La figure ci-jointe, proposée en appliquette, montre un montage de type Cassegrain. Le diamètre du miroir primaire vaut 128 cm.
Positionner graphiquement la lentille équivalente du télescope, et déterminer ensuite sa focale équivalente.
[2 points]
Calculer le nombre d'ouverture du télescope.
[1 points]
La forme des miroirs doit s'approcher au mieux de la forme idéale (parabolique, hyperbolique, plane...). A grande comme à petite échelle, aucun défaut ne doit excéder une limite, dont la valeur dépend des performances souhaitées.
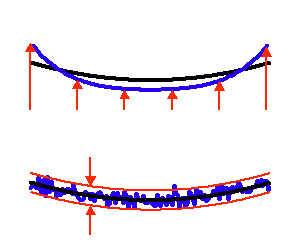
Plutôt que de confier la forme idéale du collecteur à une position statique et rigide, l'optique active préfère inclure une chaîne de correction commandant la forme idéale du miroir au moyen d'actuateurs positionnant idéalement chaque sous-élément du miroir.
Cette technique est employée p.ex. pour les miroirs de 8.2 m du VLT. Si leur forme idéale devait découler de leur seule rigidité, ces miroirs auraient une épaisseur supérieure à 2 m : solution inadaptée. Les miroirs sont minces (18 cm) ; leur faible épaisseur leur assure une certaine souplesse, et quelle que soit leur position, des actuateurs les repositionnent pour une forme idéale.
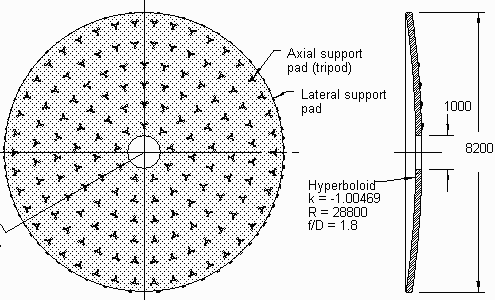
Dans le domaine radio, caractérisé par des longueurs d'onde relativement grandes, un grillage peut suffire à constituer un bon miroir. Il est vu par l'onde tel une surface pleine, et sa forme rapportée à la longueur d'onde considérée est suffisamment précise.
ObjectifsL'étude technologique des qualités optiques des éléments des collecteurs astronomiques s'appuie sur de multiples domaines non ici explorés. On s'intéresse essentiellement à la forme géométrique idéale des collecteurs, en laissant de côté : les aberrations, les propriétés thermomécaniques des miroirs et de leurs supports, les propriétés de réflexion des surfaces ; la transmission dans les verres des lentilles...
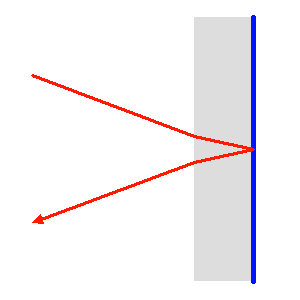
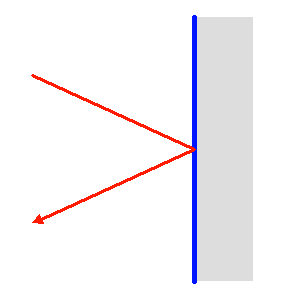
Un miroir optique diffère d'un miroir usuel. Un miroir usuel est constitué d'une plaque de verre protégeant une feuille métallique réfléchissante. Le faisceau optique traverse par 2 fois cette vitre, avant et après la réflexion métallique.
Un miroir astronomique est constitué d'un support vitreux, précisément taillé, recouvert d'une très fine couche métallique réfléchissante (aluminium, argent ou or principalement, selon le domaine de longueurs d'onde utilisé), éventuellement protégée d'une mince couche d'oxyde. Le faisceau optique ne traverse pas le verre.
Le substrat en verre est typiquement du zérodur, verre se caractérisant par un très faible coefficient de dilatation thermique.
La qualité des optiques de toute la chaîne de détection est essentielle. Elle se traduit par la fonction d'étalement du point, qui rend compte de l'image d'un objet ponctuel à l'infini.
Cette qualité, pour un miroir, se résume souvent à un paramètre : à grande ou à petit échelle, le miroir ne doit pas s'écarter de sa forme idéale de plus d'une fraction de longueur d'onde (typiquement de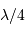 
pour un dioptre usuel à 
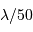pour une optique d'interféromètre).
On appelle optique active un système restituant la forme idéale des surfaces collectrices non de façon statique, avec des miroirs très rigides, mais dynamique, avec des miroirs minces positionnés par des actuateurs. L'optique active corrige les déformations lentes d'origine thermique et mécanique.
L'optique adaptative corrige en temps réel les défauts du front d'onde induits par la turbulence. Voir les pages dédiées à l'optique adaptative.
Les diamètres collecteurs ont régulièrement augmenté au cours du temps, pour collecter plus, et plus précisément, de photons. Divers projets de télescopes optiques de miroir primaire de 30 à 50 m sont dans les cartons. Des structures de telles dimensions existent déjà, mais dans le domaine radio, avec des longueurs d'onde centimétriques et non submicrométriques.
Le projet CELT illustre les caractéristiques des futurs projets. Le projet OWL de l'ESO, préparant la classe des télescopes de 100 m, n'a pas abouti, car il supposait un trop radical changement d'échelle. Il a été remplacé par un projet de télescope de 39 mètres de diamètre, l'Extremely Large Telescope (ELT) de l'Observatoire Européen Austral, dont la première lumière est prévue en 2024.
ObjectifsDévoiler les grandes lignes des projets de grands observatoires.
Certains besoins scientifiques (pas tous) nécessitent la collecte de flux de plus en plus faible, et donc des collecteurs encore plus grands que ceux de la classe 10 m entrés en action dans les années 1990.
Les télescope de cette classe 10 m ont montré des changements importants par rapport à leurs prédécesseurs, induits simplement par leur taille.
Ces principes sont conservés pour les projets de télescope de la classe 30 m, avec en plus la généralisation des miroirs segmentés.
Si le principe des très grands télescopes est mûr, leur réalisation pratique pose de nombreux problèmes. Par exemple :
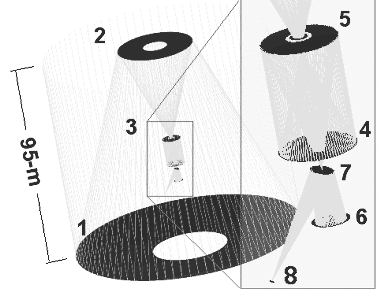
Une solution alternative aux très grands télescopes pourrait consister à réaliser une surface collectrice avec plusieurs pupilles reconstituant une seule surface collectrice, mais non entièrement pavée ; un système optique apporte la densification de pupilles, et conduit au principe de l'hypertélescope. La réalisation pratique d'un hypertélescope n'est pas prévue dans un futur proche, un certain nombre de points durs techniques subsistant encore.
HypertélescopeDifficulté : ☆☆☆ Temps : 60 min
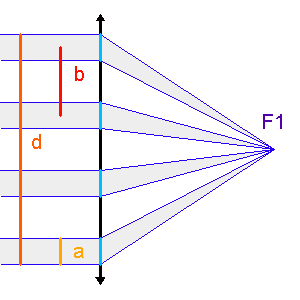
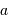mesure le diamètre d'une sous-pupille, 
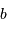l'écartement entre 2 sous-pupilles et 
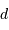le diamètre total.
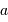mesure le diamètre d'une sous-pupille ; 
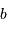leur écartement.
La première figure donne le schéma
de principe d'un hypertélescope. L'équivalent du miroir primaire
est constitué de sous-pupilles, reconstituant de façon incomplète
une surface collectrice correspondant à une immense parabole.
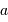mesure le diamètre d'une sous-pupille ; 
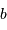leur écartement.
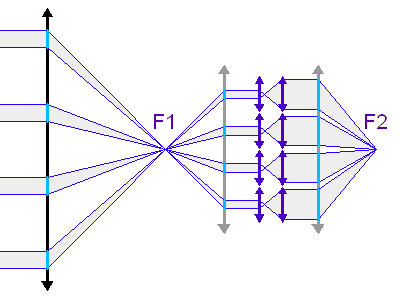
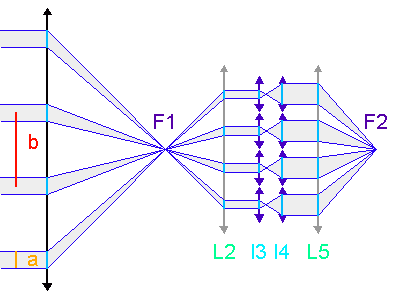
La deuxième figure présente le montage du densificateur de pupille. Les lentilles L2 et L5 sont supposées identiques, si bien que le grossissement du système constitué de ces lentilles vaut -1 ; le grossissement angulaire du système afocal constitué des lentilles l3 et l4 est noté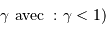 
.
Cet exercice est à résoudre sans gros calcul ! Pour simplifier l'approche, on travaille sur une seule dimension, comme le montre la figure (sans chercher à reconstituer la surface collectrice).
On s'intéresse juste à l'optique en amont de F1. Quels paramètres
dimensionnent la taille angulaire de la tache image en F1 d'une
sous-pupille, de l'ensemble des sous-pupilles ? Mener l'analogie avec un réseau d'interférence composé de fentes de largeur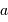 
séparées d'une distance 
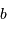, s'étalant sur une longueur totale 
.
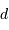Déterminer l'action du système (l3, l4), en comparant les situations en F1 et F2.
Quel est l'intérêt du système ? Que se passe-t-il lorsque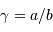 
?
Qu'a-t-on gagné, qu'a-t-on perdu avec cette opération ?
pages_collecter/elt-sexercer.html
Réfléchir au rôle de la diffraction par une sous-pupille, à celui des interférences entres sous-pupilles.
Mener l'analogie avec un réseau.
L'analogie avec un réseau de diffraction est immédiate. Une
sous-pupille se comportant comme une fente individuelle d'un
réseau de diffraction. Chaque sous-pupille diffracte le faisceau
pour une tache image individuelle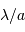 
; les
interférences entre les sous-faisceaux conduisent à une taille
angulaire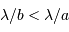 
.
Pour une comparaison aisée, imaginer que L2 et L5 ont les mêmes diamètre et focale que L1.
La recombinaison des faisceaux par L5 conduit à un système qui aurait des caractéristiques identiques à L1, mais en remplaçant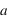 
par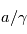 
, c'est-à-dire, de façon équivalente, en remplaçant 
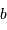par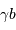 
. Tout se passe comme si on avait un gruyère avec moins de trous.
En exagérant la taille des lentilles L2 et L5, jusqu'à celle de L1, on peut comparer directement les situations de
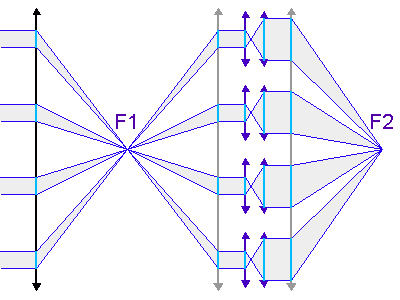
Mener un raisonnement géométrique s'appuyant sur la figure.
S'intéresser à la localisation de l'énergie dans les pics d'interférence.
Lorsque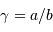 
, tout se passe comme si l'on avait réuni des collecteurs de diamètre plus important et qu'il n'y avait plus de trous dans le miroir équivalent. La pupille a été densifiée.
S'intéresser à la tache de diffraction.
S'intéresser au champ accessible, dimensionné par une tache de diffraction élémentaire
Que devient la tache de diffraction d'une sous-pupille ?
Le gain en termes de formation d'image est clair : on a reconstitué un plus grand miroir, et donc les images sont plus piquées (la fonction d'étalement du point est moins... étalée). Mais, comme la tache de diffraction d'une
sous-pupille a été divisée par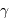 
. Il en est de même du champ : le champ accessible par l'instrument a été réduit. Il y a toujours des compromis à faire.