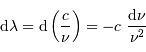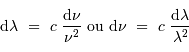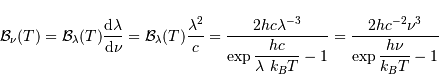Spectres de corps noirs
L'observation de spectres stellaires, à basse
résolution spectrale montre que l'allure
de ces spectres suit effectivement celle d'un corps noir.
Spectres de corps noirs
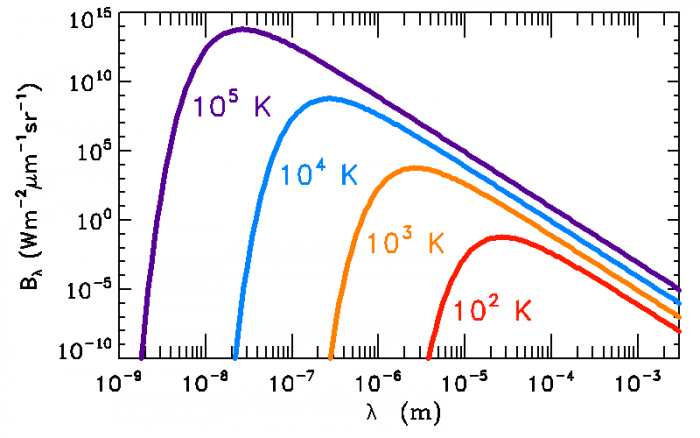
Spectres de corps noirs à différentes températures
Crédit :
ASM
Spectres stellaires
Cela n'est vrai que pour l'allure du spectre : à plus haute résolution,
il apparaît clairement que se superposent à l'enveloppe du corps noir
des raies en absorption. Si le spectre de corps noir ne dépend que de la
température d'équilibre du corps, les raies signent la présence des
éléments constitutifs de l'atmosphère stellaire.
Le spectre des étoiles chaudes s'écarte significativement de la courbe du corps noir, en raison de l'ionisation de l'hydrogène par des photons de longueur d'onde inférieure à 360 nm.
Spectre stellaire
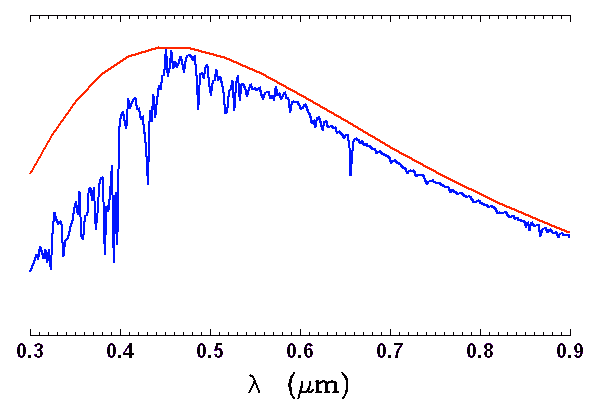
Spectre stellaire (type G2) à basse résolution. Il se superpose approximativement
à un spectre de corps noir de température 5700 K, sauf dans le domaine UV.
Crédit :
ASM
Spectre stellaire
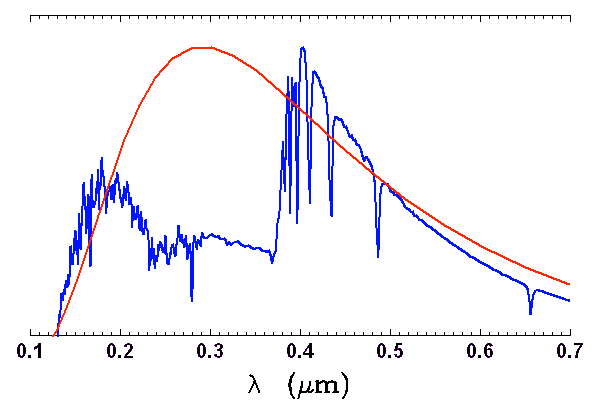
Spectre d'une étoile chaude (type G1) à basse résolution. L'absorption intense en deçà de 360 nm, due à l'ionisation de l'hydrogène, ecarte le spectre de l'enveloppe du corps noir.
Crédit :
ASM
 Objectifs
Objectifs
- Définir le rayonnement du corps noir
- Le corps est finalement une entité physique idéale, dont le rayonnement ne
se caractérise plus que par sa température d'équilibre
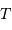
- Les définitions des grandeurs énergétiques utiles sont rappelées à la page de photométrie énergétique.
Courbes de lumière de corps noirs
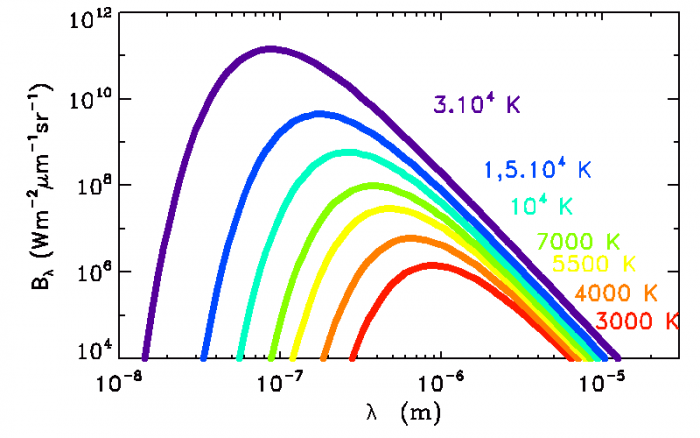
Luminance monochromatique du corps noir, pour des températures
correspondant à divers types stellaires
Crédit :
ASM
Le dénominateur de la loi de Planck est caractéristique d'une loi
statistique de Bose-Einstein, à laquelle obéit un gaz de photons. Comme
tout vecteur d'interaction fondamentale (l'interaction
électromagnétique), le photon est un boson, une particule de spin entier.
La fonction 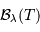 dépend de la température comme de la
longueur d'onde. Elle est notée ainsi, et non
dépend de la température comme de la
longueur d'onde. Elle est notée ainsi, et non 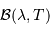 ,
pour mettre en évidence la variable spectrale, ici la longueur d'onde.
Cette dépendance spectrale peut également s'exprimer en fonction non de la
longueur d'onde, mais de la fréquence. La loi de Planck se réécrit alors
dans ce cas (justification donnée en
exercice).
,
pour mettre en évidence la variable spectrale, ici la longueur d'onde.
Cette dépendance spectrale peut également s'exprimer en fonction non de la
longueur d'onde, mais de la fréquence. La loi de Planck se réécrit alors
dans ce cas (justification donnée en
exercice).
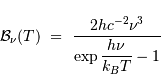
L'unité de 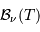 est alors :
est alors :
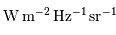 .
.
Courbe de rayonnement
A l'aide de l'appliquette ci-dessous, vous pouvez tracer un spectre de corps noir en fonction de sa température.

 Luminances spectrales
Luminances spectrales
Difficulté : ☆
Temps : 20 min
Question 1)
On considère la luminance du corps noir, dans un domaine spectral de
largeur 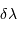 autour de la longueur d'onde
autour de la longueur d'onde 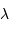 .
Exprimer les fréquence et intervalle de fréquence correspondant.
.
Exprimer les fréquence et intervalle de fréquence correspondant.
La relation entre fréquence et longueur d'onde du rayonnement s'écrit :
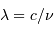
Question 2)
Exprimer la luminance du corps noir de 2 manières
différentes, en fonction de ce qui précède.
La luminance correspond à la luminance spectrale intégrée sur un
intervalle spectral
La conservation de l'énergie conduit à égaler les expressions trouvées
pour la luminance, fonction de 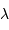 ou
ou 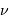 .
.
Rappel
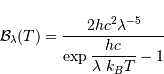
- Question 1
Aide :
La relation entre fréquence et longueur d'onde du rayonnement s'écrit :
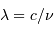
Aide :
La relation entre 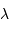 et
et 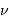 donne celle entre les intervalles
spectraux
donne celle entre les intervalles
spectraux 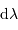 et
et 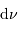 , par différentiation.
, par différentiation.
Solution :
La relation entre fréquence et longueur d'onde du rayonnement s'exprime
: 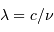 . On en déduit :
. On en déduit :
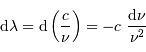
Le signe négatif rappelle que les
échelles en longueur d'onde et fréquence sont inversées. Par la suite,
avec une définition adéquate des bornes de l'intervalle, on écrit :
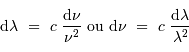
- Question 2
Aide :
La luminance correspond à la luminance spectrale intégrée sur un
intervalle spectral
Aide :
La conservation de l'énergie conduit à égaler les expressions trouvées
pour la luminance, fonction de 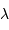 ou
ou 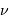 .
.
Aide :
Rappel
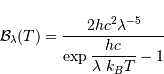
Solution :
La luminance, intégrée sur l'intervalle spectral,
s'écrit donc de 2 façons différentes, qui doivent rendre compte de la
même énergie dans l'intervalle spectral considéré :
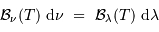
d'où
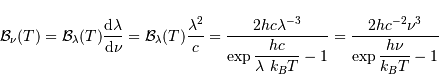
La correspondance est établie.



 :
:
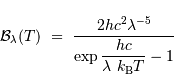
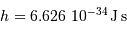 , la constante de Boltzmann
, la constante de Boltzmann 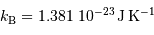 , et
, et 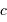 la célérité de la lumière dans le vide. Ceci indique que la loi de Planck est à l'intersection, respectivement, de la physique quantique, statistique et relativiste.
la célérité de la lumière dans le vide. Ceci indique que la loi de Planck est à l'intersection, respectivement, de la physique quantique, statistique et relativiste.
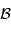 s'exprime en
s'exprime en 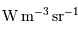 , ou en unité
dérivée
, ou en unité
dérivée 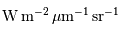 ;
; 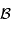 est une
est une

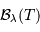 dépend de la température comme de la
longueur d'onde. Elle est notée ainsi, et non
dépend de la température comme de la
longueur d'onde. Elle est notée ainsi, et non 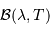 ,
pour mettre en évidence la variable spectrale, ici la longueur d'onde.
Cette dépendance spectrale peut également s'exprimer en fonction non de la
longueur d'onde, mais de la fréquence. La loi de Planck se réécrit alors
dans ce cas (justification donnée en
,
pour mettre en évidence la variable spectrale, ici la longueur d'onde.
Cette dépendance spectrale peut également s'exprimer en fonction non de la
longueur d'onde, mais de la fréquence. La loi de Planck se réécrit alors
dans ce cas (justification donnée en
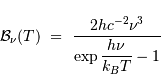
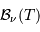 est alors :
est alors :
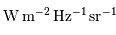 .
.

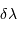 autour de la longueur d'onde
autour de la longueur d'onde 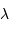 .
Exprimer les fréquence et intervalle de fréquence correspondant.
.
Exprimer les fréquence et intervalle de fréquence correspondant.
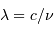
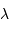 et
et 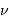 donne celle entre les intervalles
spectraux
donne celle entre les intervalles
spectraux 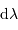 et
et 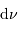 , par différentiation.
, par différentiation.
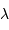 ou
ou 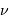 .
.
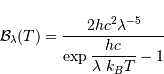
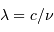 . On en déduit :
. On en déduit :