Apprendre

Prérequis

Diffraction de Fraunhofer. Diffraction par une fente rectiligne.

Objectifs

Déterminer et dimensionner le rôle de la diffraction dans la formation d'image.

Tache image pour un collecteur de section circulaire

Définition

La demi-largeur angulaire de la tache centrale de diffraction obtenue à la longueur d'onde 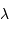$\lambda$ pour un collecteur de diamètre 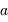vaut :

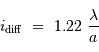
$i _{\mathrm{diff}} \ = \ 1.22\ {\lambda \over a}$

Le facteur 1.22 est d'origine géométrique (dans le cas d'une fente rectiligne de largeur 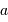, le facteur est 1) ; c'est la première valeur qui annule la fonction de Bessel qui rend compte de la diffraction par une pupille circulaire.

Il est physiquement impossible de distinguer des détails plus petits que cette tache image : la diffraction fixe la résolution ultime d'un collecteur unique.

Pour comparer la tache de diffraction au diamètre angulaire des objets étudiés, il est utile de connaître l'ordre de grandeur :

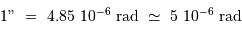
$1"\ = \ 4.85 \ 10^{-6}\ \mathrm{rad}\ \simeq\ 5\ 10^{-6}\ \mathrm{rad}$

et aussi

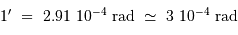
$1'\ = \ 2.91 \ 10^{-4}\ \mathrm{rad}\ \simeq\ 3\ 10^{-4}\ \mathrm{rad}$

De l'intérêt d'un collecteur de grand diamètre

La relation entre la taille angulaire de la tache image et le diamètre du collecteur montre directement l'intérêt d'augmenter ce dernier : cela permet d'avoir des images angulairement mieux résolues.