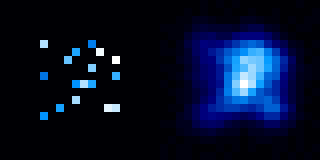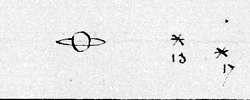
Saturne, et ses satellites, observés par
J.D. Cassini en 1673, confondus avec des étoiles.
Crédit :
Bibliothèque de l'Observatoire de Paris
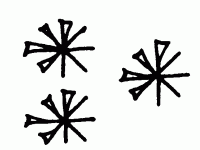
Le mot étoile codé en écriture cunéiforme.
Crédit :
ASM

Mizar, dans la Grande Ourse : diffraction, turbulence, surexposition, réflexions parasites s'ajoutent et s'emmêlent.
Crédit :
CDS
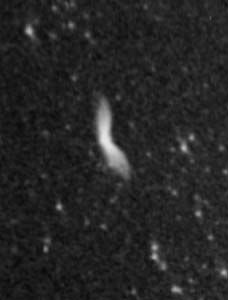
Le défaut de coma apparaît en tout point éloigné du centre optique. L'image d'un tel point s'allonge ; elle apparaît telle une petite comète, d'où le nom de cette aberration optique.
Crédit :
D. Césari
L'image d'un point
L'astrophysique nous apprend que les étoiles sont des sphères gazeuses, tellement lointaines qu'il est impossible dans la plupart des cas de les résoudre spatialement. Pourquoi alors les représente-t-on et les voit-on avec diverses formes tellement différentes d'un point ou d'un cercle, mais le plus souvent proches du symbole  ?
?
En fait, plusieurs phénomènes se conjuguent pour aboutir à ces formes
et les expliquer :
- Les aberrations optiques diverses, qui déforment l'image géométrique perçue : coma, défaut de mise au point.
- La diffraction, qui fait que l'image d'un point ne peut pas être un point
- La turbulence atmosphérique, qui brouille l'information spatiale
- Les propriétés des récepteurs.

Exemple de fonction d'étalement du point de l'instrument NAOS. Avec correction d'optique adaptative, la FEP se rapproche d'une figure d'Airy.
Crédit :
LESIA
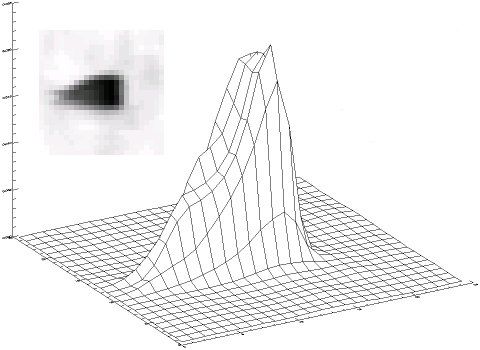
Fonction d'étalement du point de la voie exoplanète du satellite CoRoT.
Crédit :
CNES
Fonction d'étalement du point
L'image d'un objet ponctuel, non ponctuelle, est donnée par la fonction de transfert de la chaîne de détection. Cette fonction de transfert, dans ce cas précis, s'appelle fonction d'étalement du point, soit FEP en français ou PSF en anglais (point spread function).
Connaître ou estimer la fonction d'étalement du point est une étape indispensable pour le traitement d'image. Autre exemple : la FEP d'une image obtenue par le satellite CoRoT.
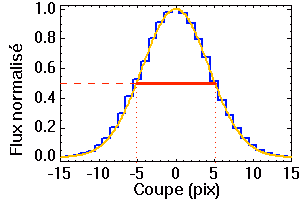
Définition de la largeur à mi-hauteur.
Crédit :
ASM
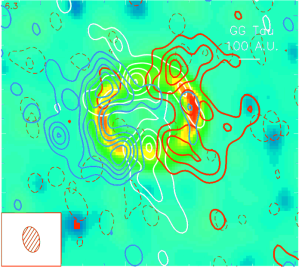
La tache image est explicitement indiquée sur l'
image de la
source GG Tauri enregistrée dans la raie de
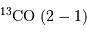
. Cette source correspond à un système stellaire binaire en formation. Le flux millimétrique à 1.3 mm codé en fausse couleur montre une structure en anneau.
Crédit :
IRAM
Largeur à mi-hauteur
On rend compte d'une fonction d'étalement du point simple par sa largeur à mi-hauteur.
Souvent, les images obtenues dans les longueurs d'onde millimétriques ou radio
mentionnent explicitement l'extension à mi-hauteur de la tache image élémentaire.

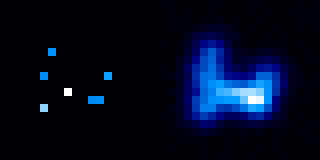
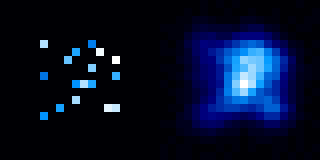
Simulation de champs stellaires. L'étalement de l'image de plusieurs sources ponctuelles bien distinctes peut conduire à l'apparence d'une source étendue.
Crédit :
ASM
FEP et résolution spatiale
La résolution spatiale dépend intimement de la FEP : distinguer les détails d'un champ s'avère impossible aux échelles plus petites que la largeur à mi-hauteur de la FEP.
 Objectifs
Objectifs
La fonction de transfert, l'image d'un objet ponctuel, transcrit la qualité de la formation d'image.

Fragment d'image, et estimation de sa fonction d'étalement du point.
Les différentes images des sources stellaires correspondent à la convolution de l'image idéale stellaire par la
FEP.
Crédit :
ASM
Fonction de transfert/fonction d'étalement du point
La fonction de transfert de la chaîne de collecte du signal, ou fonction d'étalement du point, rend compte de l'image non ponctuelle d'un objet ponctuel. Cette fonction de transfert relate toutes les modifications apportées à l'image idéale.
Par définition, l'image d'une source ponctuelle est la fonction de transfert, au bruit près.
L'image d'une source non ponctuelle est son image géométrique idéale convoluée par la fonction de transfert. Au mieux, la fonction de transfert rend compte de la diffraction. Mais elle inclut aussi tous les autres défauts de la chaîne de détection.
Résolution, et largeur à mi-hauteur
Le lien entre la fonction de transfert et la résolution est immédiat : il n'est pas possible d'obtenir de détails plus fins que la fonction de transfert.
Il est souvent suffisant de rendre compte de la fonction de transfert, si elle présente la symétrie circulaire, par sa largeur à mi-hauteur.
Contributions à la fonction d'étalement du point
Les pages suivantes décrivent la contribution de la diffraction à la fonction de transfert. Les aberrations optiques ne sont pas abordées. Le rôle de la turbulence atmosphérique est traité dans une section à part.
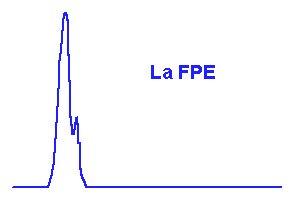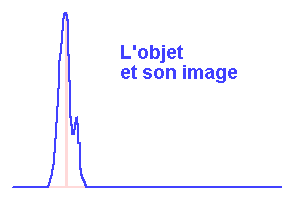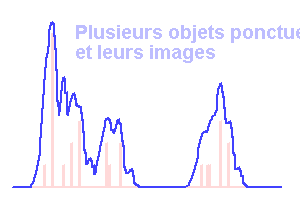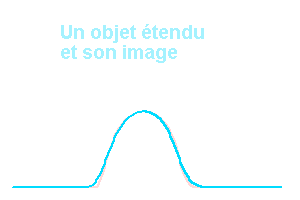
FPE, objets et images.
Crédit :
ASM
La fonction d'étalement du point à l'oeuvre
L'animation ci-dessous décompose, dans un cas unidimensionnel, la transformation d'un objet en son image via la FPE.



 ?
?




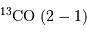 . Cette source correspond à un système stellaire binaire en formation. Le flux millimétrique à 1.3 mm codé en fausse couleur montre une structure en anneau.
. Cette source correspond à un système stellaire binaire en formation. Le flux millimétrique à 1.3 mm codé en fausse couleur montre une structure en anneau.