Que l'observation astrophysique serait facile si l'image d'un point était un point !
Dans le meilleur des cas, l'image d'une étoile est une tache de diffraction, mais le plus souvent, c'est une structure spatialement et temporellement bien plus complexe.
Le but de cette section est de comprendre et d'interpréter la structure spatiale d'une image simple.

Représentation des Pléiades, à l'époque néo-babylonienne, en 200 avant JC. Les étoiles ont une forme... d'étoile
!
Crédit :
ASM
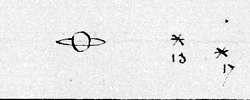
Saturne, et ses satellites, observés par
J.D. Cassini en 1673, confondus avec des étoiles.
Crédit :
Bibliothèque de l'Observatoire de Paris
Le mot étoile codé en écriture cunéiforme.
Crédit :
ASM

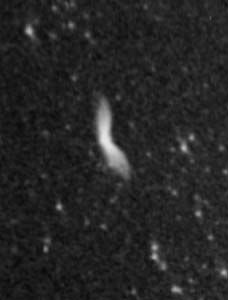
Mizar, dans la Grande Ourse : diffraction, turbulence, surexposition, réflexions parasites s'ajoutent et s'emmêlent.
Crédit :
CDS
Le défaut de coma apparaît en tout point éloigné du centre optique. L'image d'un tel point s'allonge ; elle apparaît telle une petite comète, d'où le nom de cette aberration optique.
Crédit :
D. Césari
L'image d'un point
L'astrophysique nous apprend que les étoiles sont des sphères gazeuses, tellement lointaines qu'il est impossible dans la plupart des cas de les résoudre spatialement. Pourquoi alors les représente-t-on et les voit-on avec diverses formes tellement différentes d'un point ou d'un cercle, mais le plus souvent proches du symbole  ?
?
En fait, plusieurs phénomènes se conjuguent pour aboutir à ces formes
et les expliquer :
- Les aberrations optiques diverses, qui déforment l'image géométrique perçue : coma, défaut de mise au point.
- La diffraction, qui fait que l'image d'un point ne peut pas être un point
- La turbulence atmosphérique, qui brouille l'information spatiale
- Les propriétés des récepteurs.

Exemple de fonction d'étalement du point de l'instrument NAOS. Avec correction d'optique adaptative, la FEP se rapproche d'une figure d'Airy.
Crédit :
LESIA
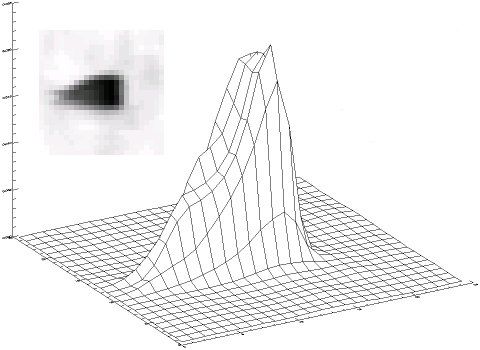
Fonction d'étalement du point de la voie exoplanète du satellite CoRoT.
Crédit :
CNES
Fonction d'étalement du point
L'image d'un objet ponctuel, non ponctuelle, est donnée par la fonction de transfert de la chaîne de détection. Cette fonction de transfert, dans ce cas précis, s'appelle fonction d'étalement du point, soit FEP en français ou PSF en anglais (point spread function).
Connaître ou estimer la fonction d'étalement du point est une étape indispensable pour le traitement d'image. Autre exemple : la FEP d'une image obtenue par le satellite CoRoT.
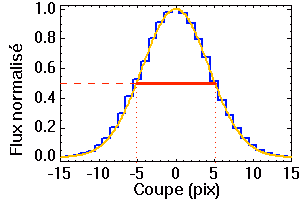
Définition de la largeur à mi-hauteur.
Crédit :
ASM
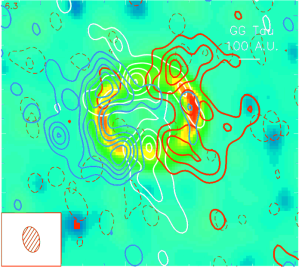
La tache image est explicitement indiquée sur l'
image de la
source GG Tauri enregistrée dans la raie de
. Cette source correspond à un système stellaire binaire en formation. Le flux millimétrique à 1.3 mm codé en fausse couleur montre une structure en anneau.
Crédit :
IRAM
Largeur à mi-hauteur
On rend compte d'une fonction d'étalement du point simple par sa largeur à mi-hauteur.
Souvent, les images obtenues dans les longueurs d'onde millimétriques ou radio
mentionnent explicitement l'extension à mi-hauteur de la tache image élémentaire.

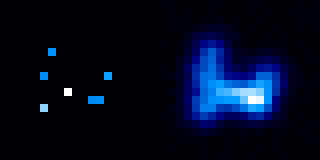
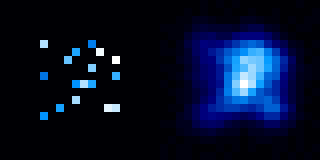
Simulation de champs stellaires. L'étalement de l'image de plusieurs sources ponctuelles bien distinctes peut conduire à l'apparence d'une source étendue.
Crédit :
ASM
FEP et résolution spatiale
La résolution spatiale dépend intimement de la FEP : distinguer les détails d'un champ s'avère impossible aux échelles plus petites que la largeur à mi-hauteur de la FEP.
 Objectifs
Objectifs
La fonction de transfert, l'image d'un objet ponctuel, transcrit la qualité de la formation d'image.

Fragment d'image, et estimation de sa fonction d'étalement du point.
Les différentes images des sources stellaires correspondent à la convolution de l'image idéale stellaire par la
FEP.
Crédit :
ASM
Fonction de transfert/fonction d'étalement du point
La fonction de transfert de la chaîne de collecte du signal, ou fonction d'étalement du point, rend compte de l'image non ponctuelle d'un objet ponctuel. Cette fonction de transfert relate toutes les modifications apportées à l'image idéale.
Par définition, l'image d'une source ponctuelle est la fonction de transfert, au bruit près.
L'image d'une source non ponctuelle est son image géométrique idéale convoluée par la fonction de transfert. Au mieux, la fonction de transfert rend compte de la diffraction. Mais elle inclut aussi tous les autres défauts de la chaîne de détection.
Résolution, et largeur à mi-hauteur
Le lien entre la fonction de transfert et la résolution est immédiat : il n'est pas possible d'obtenir de détails plus fins que la fonction de transfert.
Il est souvent suffisant de rendre compte de la fonction de transfert, si elle présente la symétrie circulaire, par sa largeur à mi-hauteur.
Contributions à la fonction d'étalement du point
Les pages suivantes décrivent la contribution de la diffraction à la fonction de transfert. Les aberrations optiques ne sont pas abordées. Le rôle de la turbulence atmosphérique est traité dans une section à part.
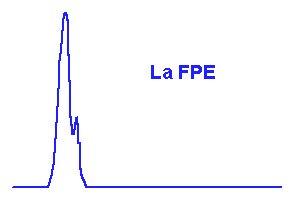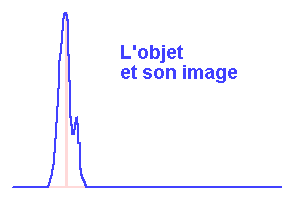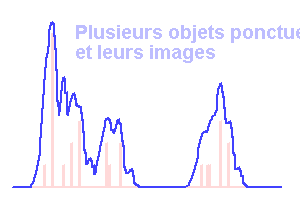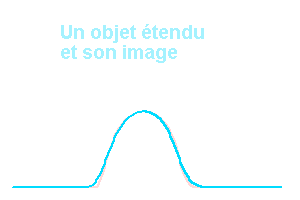
FPE, objets et images.
Crédit :
ASM
La fonction d'étalement du point à l'oeuvre
L'animation ci-dessous décompose, dans un cas unidimensionnel, la transformation d'un objet en son image via la FPE.

Image d'une étoile de l'amas ouvert NGC 188. Cet amas d'étoiles a servi pour l'étalonnage de la fonction d'étalement du point du télescope spatial Hubble. La tache image rend essentiellement compte de la figure de diffraction d'une source ponctuelle.
Crédit :
HST



Différentes tailles de collecteur, et taches de diffraction associées : l'extension de la tache de diffraction est inversement proportionnelle au diamètre du collecteur.
Crédit :
ASM
Influence du secondaire

Le front d'onde incident, avec l'occultation par le miroir secondaire, et la figure de diffraction associée. A la figure de diffraction du miroir primaire se superpose celle de l'occultation secondaire.
Crédit :
ASM
Influence du miroir secondaire
Le plus souvent, le miroir secondaire occulte le faisceau incident.
Le front d'onde initial n'est pas seulement découpé par le miroir primaire, il est aussi amputé de sa partie centrale. La tache de diffraction d'un télescope possédant un miroir secondaire sur son axe optique est moins lumineuse mais plus étendue que celle du miroir primaire considéré seul. La perte de flux lumineux est due à l'occultation par le miroir secondaire d'une partie du faisceau.
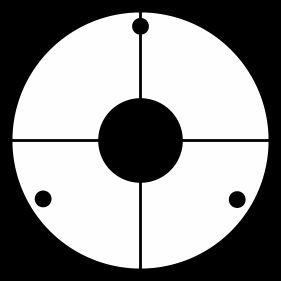
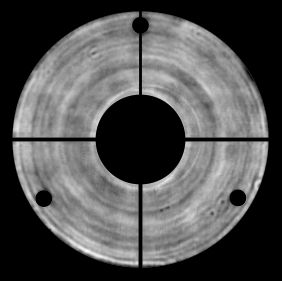
Pupille du télescope HST (théorique et observée), avec obstruction centrale du miroir secondaire, et support de celui-ci par une araignée à 4 branches.
Crédit :
IRAM
Influence de l'araignée
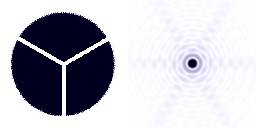
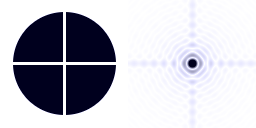

Le support du miroir secondaire, également appelé araignée, qui occulte le faisceau primaire, rajoute sa signature à la figure de diffraction.
Crédit :
ASM
Influence du support du miroir secondaire
L'araignée, le support du miroir secondaire, occulte également la pupille. Sa signature apparaît clairement pour une source brillante.
Étoile ou galaxie ?

Champ galactique avec des étoiles au premier plan. Les objets étendus, dont celui dans le coin inférieur droit, ne semblent pas présenter d'aigrettes de diffraction, contrairement aux objets ponctuels.
Crédit :
HST
Objet ponctuel ou non
Sur une image, certains objets semblent soumis à la diffraction, avec de belles aigrettes de diffraction, alors que d'autres non. Les premiers sont des objets non résolus (typiquement une étoile), alors que les seconds sont étendus (typiquement une galaxie). Les contributions des différents points sources d'un objet étendu, non superposées, sont diluées et ne se distinguent pas.
 Prérequis
Prérequis
Diffraction de Fraunhofer. Diffraction par une fente rectiligne.
 Objectifs
Objectifs
Déterminer et dimensionner le rôle de la diffraction dans la formation d'image.
Tache image pour un collecteur de section circulaire
Le facteur 1.22 est d'origine géométrique (dans le cas d'une fente rectiligne de largeur 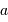 , le facteur est 1) ; c'est la première valeur qui annule la fonction de Bessel qui rend compte de la diffraction par une pupille circulaire.
, le facteur est 1) ; c'est la première valeur qui annule la fonction de Bessel qui rend compte de la diffraction par une pupille circulaire.
Il est physiquement impossible de distinguer des détails plus petits que cette tache image : la diffraction fixe la résolution ultime d'un collecteur unique.
Pour comparer la tache de diffraction au diamètre angulaire des objets étudiés, il est utile de connaître l'ordre de grandeur :
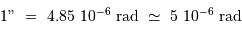
et aussi
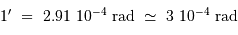
De l'intérêt d'un collecteur de grand diamètre
La relation entre la taille angulaire de la tache image et le diamètre du collecteur montre directement l'intérêt d'augmenter ce dernier : cela permet d'avoir des images angulairement mieux résolues.

Diffraction d'une onde mécanique
L'appliquette ci-jointe montre la diffraction d'une vague de surface par une ouverture étroite.

Influence du support du miroir secondaire
Le support du miroir secondaire, appelé araignée, occulte le faisceau primaire, et rajoute sa signature à la figure de diffraction, surtout pour les objets brillants.

Taches images
L'appliquette ci-dessous calcule la tache image de divers collecteurs.
Visualiser l'influence, avec un seul collecteur (avec circulaire comme choix de pupille) :
- du diamètre du collecteur,
- de la longueur d'onde (identifier la pleine échelle de la tache image, exprimée en unité angulaire),
- de l'éventuelle occultation par un miroir secondaire,
Visualiser l'influence, avec un collecteur et une occultation du secondaire (avec circ+ obst. second. comme choix de pupille) :
- de l'éventuelle occultation par un miroir secondaire,
- de la taille relative de cette occultation
Visualiser l'influence, avec plusieurs collecteurs (avec 2 circulaires ou bien croix d'Angel):
- du rapport entre leur diamètre et leur éloignement,
- de la configuration des collecteurs.
Ciel profond

Champ de galaxies.
Crédit :
HST
 Diffraction or not diffraction ?
Diffraction or not diffraction ?
Difficulté : ☆
Temps : 10 min
L'appliquette ci-jointe montre l'étoile double Mizar, dont les 2 composantes sont séparées de 14.4", observées dans le rouge à 800 nm, par un télescope de la classe 1-m.

Question 1)
Déterminer l'échelle de l'image, en "/pixel.
Établir l'échelle en se repérant par rapport au système double.
Question 2)
Déterminer le rayon des anneaux concentriques entourant chaque étoile.
Travailler avec l'outil cercle
Question 3)
Ces anneaux peuvent-ils être dus à la diffraction par le miroir primaire, secondaire (ces anneaux se situent à 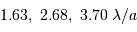 ) ?
) ?
Calculer la tache de diffraction.
 Dans quel sens ?
Dans quel sens ?
Difficulté : ☆
Temps : 20 min

Radiotélescope de Nançay : vue grand angle de l'ensemble. Le miroir plan orientable, à gauche, vise dans la direction méridienne ; le faisceau est renvoyé vers le miroir sphérique, à droite, qui le focalise au centre.
Crédit :
Observatoire de Paris

Radiotélescope de Nançay : l'antenne sphérique
Crédit :
Observatoire de Paris

Radiotélescope de Nançay : les 3 cornets de l'ancien chariot focal (en service jusqu'en 2000).
Crédit :
Observatoire de Paris
Les figures ci-jointes montrent le miroir primaire et l'ancien foyer (utilisé jusqu'en 2000) du grand radiotélescope de Nançay (Observatoire de Paris).
Question 1)
L'antenne principale a une taille de 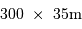 .
Estimer le profil de la tache angulaire de diffraction, pour les trois longueurs d'onde de travail 9, 18 et 21 cm (raie de couplage spin-orbite de l'hydrogène atomique).
.
Estimer le profil de la tache angulaire de diffraction, pour les trois longueurs d'onde de travail 9, 18 et 21 cm (raie de couplage spin-orbite de l'hydrogène atomique).
[2 points]
Question 3)
Discuter de la forme et de l'orientation de ces cornets.
[1 points]
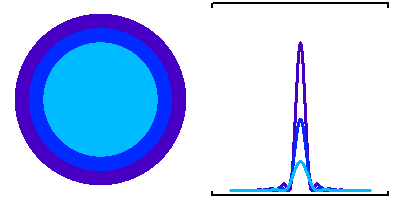
Différentes tailles de collecteur, et taches de diffraction associées.
Le flux reçu par unité d'élément d'image varie comme la puissance quatrième du diamètre collecteur.
Crédit :
ASM
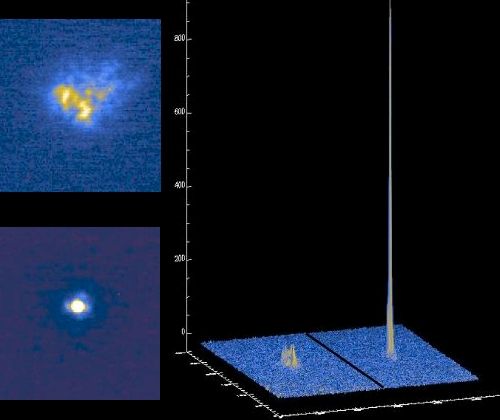
Image enregistrée sans ou avec optique adaptative.
Crédit :
ESO
De l'intérêt d'arriver à la tache de diffraction
Il est utile de s'attacher à récupérer une forte densité de flux sur les pixels, comme le montre cet exemple de traitement par optique adaptative.
Critère de Rayleigh

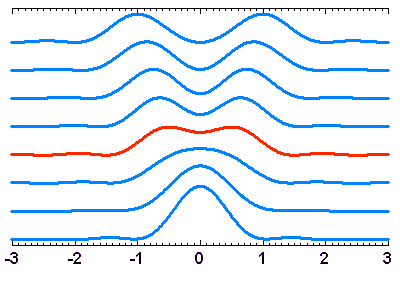
Le critère de Rayleigh ; la résolution des 2 sources (images, et coupes de ces images) nécessite une séparation de l'ordre de
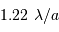
.
L'abscisse du profil en coupe est directement donnée en unité
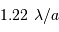
.
Crédit :
ASM
Le critère de Rayleigh
Les schémas ci-joints illustrent le critère de Rayleigh, qui définit la condition pour distinguer 2 objets de magnitude identique angulairement voisins.
 Prérequis
Prérequis
Diffraction de Fraunhofer.
 Objectifs
Objectifs
Montrer le lien entre la diffraction et la résolution ultime d'un système optique.
Critère de Rayleigh
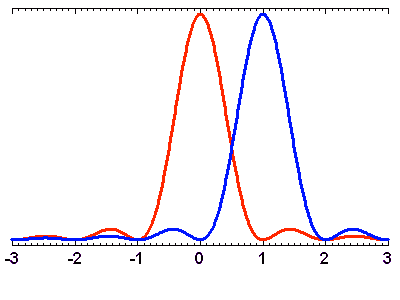
Le critère de Rayleigh ; l'abscisse est ici directement en unité
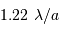
Crédit :
ASM
Critère de Rayleigh
Le critère de Rayleigh permet de préciser à quelle condition
on peut distinguer 2 sources ponctuelles : il faut que le premier zéro
de la figure de diffraction de l'une corresponde au maximum de l'autre.
 Bonnes résolutions
Bonnes résolutions
Difficulté : ☆
Temps : 10 min
On cherche à résoudre différents objets, en lumière visible. Déterminer le diamètre minimal du collecteur nécessaire, la résolution angulaire étant limitée par la diffraction, dans les cas suivants.
Question 1)
Un cratère de 20 km sur la Lune (distante de 380 000 km).
Estimer la taille angulaire du cratère, et la comparer à la résolution limitée par la seule diffraction : 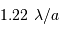
Question 2)
Une étoile double, dont les composantes sont séparées de 0.2".
Une histoire d'anneaux
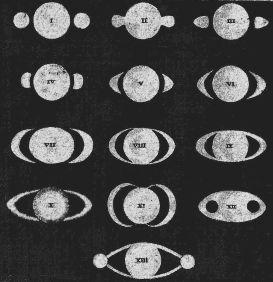
Diverses interprétations rendant compte des observations des anneaux de Saturne
(compilation d'observations de Galilée, Hévélius, Gassendi) : 2 satellites, des protubérances, des anses...
Crédit :
Bibliothèque de l'Observatoire de Paris
Cratères lunaires

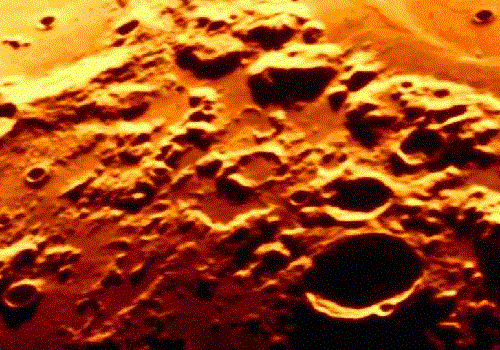
La Lune observée avec une lunette de 70 mm, et avec la caméra grand champ du télescope
CFH.
Crédit :
CFHT
Résolution angulaire et qualité d'image
L'apparence d'un objet dépend intimement de la finesse des détails les plus fins. Ainsi, l'identité des anneaux de Saturne n'a été dévoilée que lorsque des observations de qualité suffisante ont permis de trancher parmi les multiples interprétations alors discutées.
Le gain en résolution angulaire permet une meilleure identification des images ;
par exemple pour la Lune observée avec un petit collecteur, ou bien un grand collecteur corrigé des premiers ordres de la turbulence.
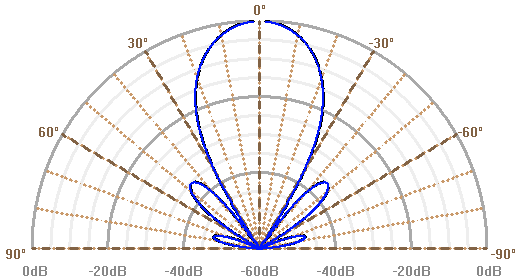
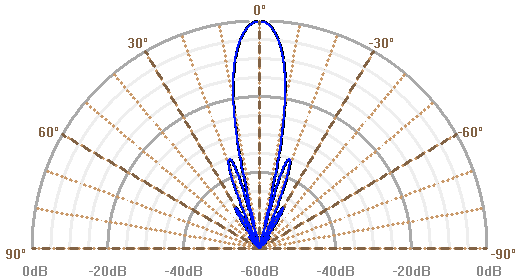
Lobes d'antenne, en diagramme polaire. L'amplitude du lobe est donnée en échelle logarithmique, mesurée en dB d'atténuation par rapport à la réponse dans l'axe.
Crédit :
ASM
Résolution angulaire et longueur d'onde
A grande longueur d'onde, la diffraction empêche une vision spatialement bien résolue, sauf à avoir un collecteur de très grande taille. Pour une antenne radio unique, circulaire de diamètre correspondant à un nombre limité de longueurs d'onde, le lobe d'antenne apparaît très étendu.
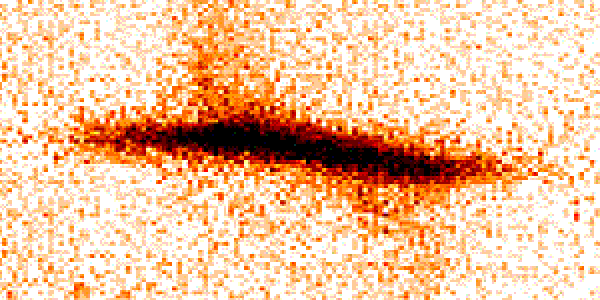
L'objet NGC7782, vu par le spectroimageur UVES du VLT (couleur en vidéo inverse). La pixélisation apparaît clairement.
Crédit :
ESO
Résolution angulaire et taille d'un élément d'image
Il est important, pour enregistrer une image en respectant sa résolution angulaire, d'avoir des éléments d'image ou pixels convenablement dimensionnés.
Vers la haute résolution angulaire
La quête de résolution angulaire de plus en plus fine nécessite des bases de collecte d'observation de plus en plus étendues. Comme la taille d'un élément collecteur est limitée (en 2018 : à 8 m en mono-pupille pour les télescopes du VLT, Gemini Nord et Sud, Subaru ; 10 m en pupille segmentée pour les 2 télescopes Keck; bientôt 39 mètres pour l'ELT européen de l'ESO), on se tourne vers l'interférométrie.
La pixélisation
La résolution angulaire ne dépend pas uniquement des conditions de collecte du signal, avec un collecteur de diamètre plus ou moins grand ; elle dépend aussi de la façon dont l'image est finalement enregistrée.
L'enregistrement du signal, aujourd'hui quasi uniquement sous forme numérique, doit être adapté à la résolution.
Afin que la taille finie des pixels ne limite pas la résolution, le critère de Shannon énonce qu'il faut au moins 2 pixels par élément de résolution.
Par exemple, si la résolution visée est de 0.4", un pixel doit couvrir 0.2".
S'il est plus gros, sa taille va limiter la résolution.
S'il est plus petit, le signal sera suréchantillonné spatialement, sans gain d'information spatiale.
Résolution angulaire variable

Animation montrant l'aspect de la galaxie M31 à diverses résolutions spatiales, balayant les différents aspects avec un appareil très peu résolvant, jusqu'à un bon télescope.
Crédit :
ASM
Résolution angulaire
L'aspect de galaxie M31 (d'Andromède) dépend de la résolution angulaire instrumentale. Plus elle est élevée, plus les détails observables sont fins.
Taille du pixel variable
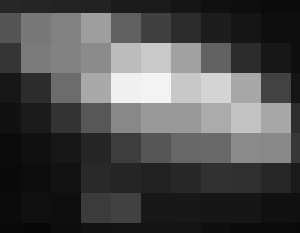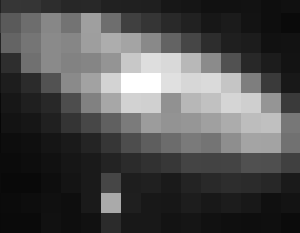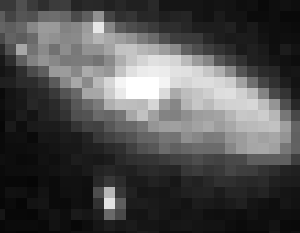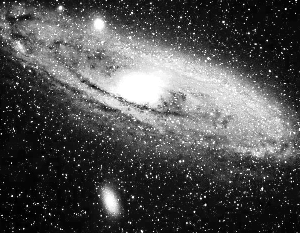
Animation montrant la galaxie M31, à divers niveaux de pixélisation. Plus la taille du
pixel est petite, meilleure est la résolution angulaire, donc la résolution spatiale.
Crédit :
ASM
Résolution angulaire et taille d'un élément d'image
La résolution est également limitée par la pixélisation, qui conditionne la FEP.
 Choix d'une caméra
Choix d'une caméra
Difficulté : ☆
Temps : 20 min
Dans le cadre du développement d'un instrument, on cherche à choisir la caméra optimale, càd celle qui réalisera les performances demandées, pour un coût minimal. Un constructeur propose
des caméras de taille 1k 1k (1000 px par 1000 px), 1k
1k (1000 px par 1000 px), 1k 2k,
2k
2k,
2k 2k, et 2k
2k, et 2k 4k, avec pixels carrés de 20, 15 ou 9 micromètres de côté.
4k, avec pixels carrés de 20, 15 ou 9 micromètres de côté.
Question 1)
Le collecteur présente un diamètre de 3.6 m, pour une ouverture f/3.3
En déduire la focale équivalente, puis le lien entre la taille physique 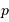 du pixel et le champ
du pixel et le champ 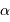 qu'il couvre.
qu'il couvre.
Revoir la relation entre ouverture, focale et diamètre.
Si 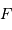 est la focale, alors
est la focale, alors 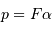
Question 2)
Le champ doit couvrir 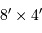 , avec une résolution de
, avec une résolution de 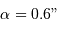 .
En déduire la caméra appropriée.
.
En déduire la caméra appropriée.
Déterminer la taille angulaire d'un pixel.
 Saturne et ses anneaux
Saturne et ses anneaux
Difficulté : ☆☆
Temps : 15 min

Géométrie simplifiée.
Crédit :
ASM
L'identification de la nature des anneaux de Saturne ne fut pas sans peine. Le but de l'exercice est de déterminer la résolution angulaire nécessaire permettant de le faire.
A l'opposition, Saturne s'approche à 8.5 UA de la Terre. Le rayon planétaire vaut 60 000 km, les rayons interne et externe des principaux anneaux respectivement 90 000 et 140 000 km. On suppose que les anneaux sont observés sous grand incidence (l'incidence maximale est de l'ordre de 26 deg), pour être dans un cas favorable (lorsque la Terre passe dans le plan des anneaux... on ne les voit simplement pas). Néanmoins, pour simplifier les calculs, on s'intéresse au seul problème 1-D portant sur la seule variable radiale, selon la géométrie de la figure jointe.
Question 1)
Refaire à l'échelle schéma de Saturne et de ses anneaux. Déterminer le plus petit élément bien contrasté à observer pour pouvoir identifier les anneaux.
[1 points]
Question 2)
La résolution devant être au-moins d'un facteur 2 plus précis que la taille du plus petit élément à identifier, déterminer la résolution nécessaire.
[2 points]
- Question 1
Aide :
Établir l'échelle en se repérant par rapport au système double.
Solution :
Le seul repère donné est la séparation des 2 composantes. Une mesure seule est entachée d'erreur. Plusieurs mesures, avec l'outil ligne donnent en pixels : 60.4 ; 59.5 ; 59.8 ; 58.2 ; 59.5 ... soit de l'ordre de  .
.
On en déduit l'échelle 0.24"/pix, ou 4.13 pix/".
- Question 2
Aide :
Travailler avec l'outil cercle
Solution :
Les mesures, avec l'outil cercle, donnent en pixels, pour l'anneau entourant la composante faible 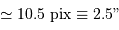 pour les anneaux entourant la composante brillante
pour les anneaux entourant la composante brillante 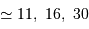 , soit respectivement 2.6, 4.1 et 7.3".
, soit respectivement 2.6, 4.1 et 7.3".
- Question 3
Aide :
Calculer la tache de diffraction.
Solution :
La tache de diffraction vaut 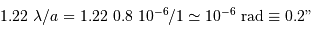 .
.
Elle est bien inférieure aux anneaux mesurés. Ils ne peuvent pas être dus à la diffraction par le miroir primaire. Ils ne semblent pas être liés à la diffraction par le miroir secondaire (de diamètre caractéristique 10 cm dans ce cas, pour coïncider au premier anneau), car leurs rayons ne progressent pas de la bonne manière. De toutes façons, la diffraction ne peut pas expliquer le fort contraste du grand anneau entourant la composante brillante ; par conséquent, des réflexions parasites sont suspectées.

 !
!
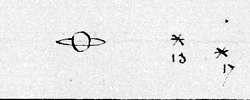



 ?
?




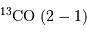 . Cette source correspond à un système stellaire binaire en formation. Le flux millimétrique à 1.3 mm codé en fausse couleur montre une structure en anneau.
. Cette source correspond à un système stellaire binaire en formation. Le flux millimétrique à 1.3 mm codé en fausse couleur montre une structure en anneau.


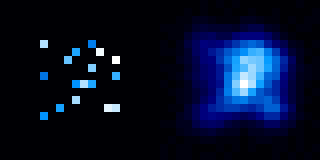













 pour un collecteur de diamètre
pour un collecteur de diamètre  vaut :
vaut :
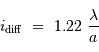
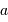 , le facteur est 1) ; c'est la première valeur qui annule la
, le facteur est 1) ; c'est la première valeur qui annule la 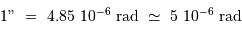
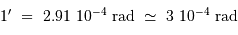


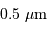 , il faut un collecteur de taille au-moins égale à
, il faut un collecteur de taille au-moins égale à
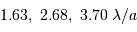 ) ?
) ?



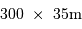 .
Estimer le profil de la tache angulaire de diffraction, pour les trois longueurs d'onde de travail 9, 18 et 21 cm (raie de couplage spin-orbite de l'hydrogène atomique).
.
Estimer le profil de la tache angulaire de diffraction, pour les trois longueurs d'onde de travail 9, 18 et 21 cm (raie de couplage spin-orbite de l'hydrogène atomique).
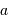
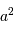
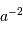
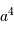




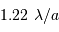 .
L'abscisse du profil en coupe est directement donnée en unité
.
L'abscisse du profil en coupe est directement donnée en unité 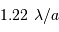 .
.
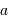
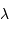
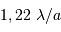

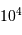

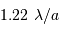
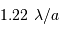







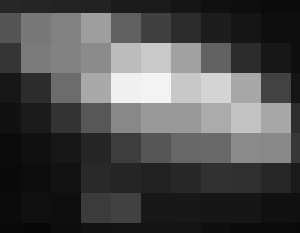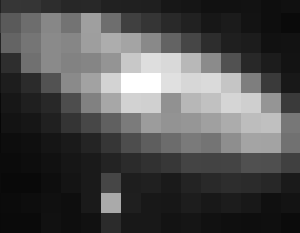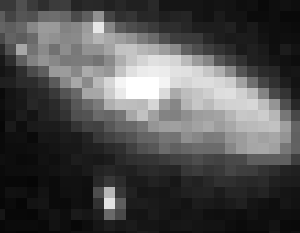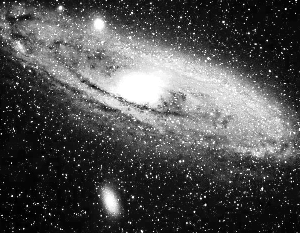
 1k (1000 px par 1000 px), 1k
1k (1000 px par 1000 px), 1k 2k,
2k
2k,
2k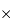 2k, et 2k
2k, et 2k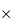 4k, avec pixels carrés de 20, 15 ou 9 micromètres de côté.
4k, avec pixels carrés de 20, 15 ou 9 micromètres de côté.
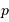 du pixel et le champ
du pixel et le champ 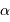 qu'il couvre.
qu'il couvre.
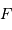 est la focale, alors
est la focale, alors 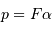
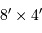 , avec une résolution de
, avec une résolution de 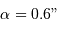 .
En déduire la caméra appropriée.
.
En déduire la caméra appropriée.

 .
.
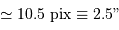 pour les anneaux entourant la composante brillante
pour les anneaux entourant la composante brillante 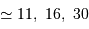 , soit respectivement 2.6, 4.1 et 7.3".
, soit respectivement 2.6, 4.1 et 7.3".
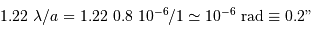 .
.
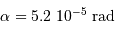 , soit environ 11".
, soit environ 11".
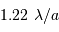 ; soit le diamètre :
; soit le diamètre :
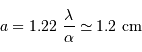
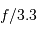 pour un collecteur de 3.6 m représente une focale de
pour un collecteur de 3.6 m représente une focale de
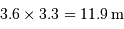 .
.
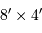 , ou
, ou 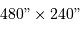 , devient, traduit en pixel,
, devient, traduit en pixel,
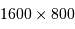 .
.
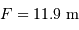 , la résolution de 0.3", cad
, la résolution de 0.3", cad 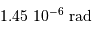 , correspond à une dimension physique de
, correspond à une dimension physique de 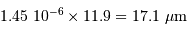 .
.
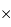 2k, avec des pixels de
2k, avec des pixels de 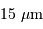 .
.