
|
Difficulté : ☆ Temps : 30 min
On considère l'étoile double AR Lacertae, dont on a observé la courbe de lumière et les vitesses radiales des deux composantes. La période du système vaut 1.983 j.
Commenter la forme des deux minima. Les températures des 2 étoiles peuvent-elles être identiques ?
[3 points]
Justifier que l'inclinaison est proche de 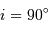 et que les orbites sont circulaires.
et que les orbites sont circulaires.
[3 points]
Représenter schématiquement les positions de l'étoile compagnon sur l'orbite relative en fonction des phases d'éclipse observées sur la courbe de lumière.
[2 points]
A l'aide de l'appliquette, estimer la durée de la phase de totalité, celle de l'éclipse principale dans son ensemble, ainsi que la profondeur (en magnitude) du minimum primaire.
[2 points]
Difficulté : ☆ Temps : 30 min
On se propose d'analyser la courbe de lumière de AR Lacertae pour en déduire les paramètres physiques des deux composantes : rayons, températures, éclats apparents et luminosités intrinsèques...
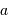 mesurant la séparation des deux étoiles,
mesurant la séparation des deux étoiles, 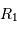 le rayon de la plus grosse,
le rayon de la plus grosse, 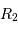 celui de la plus petite, déterminer
celui de la plus petite, déterminer 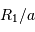 et
et 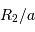 à partir de la figure.
à partir de la figure.
[2 points]
Préciser laquelle des deux étoiles est la plus chaude.
[1 points]
Déterminer le rapport des luminosités 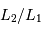 des deux étoiles. Commenter.
des deux étoiles. Commenter.
Aide [2 points]
L'étude spectroscopique de l'étoile 1 indique que son type spectral est K0 et sa classe de luminosité IV (sous-géante). Sa magnitude absolue peut donc être estimée à 3. Déterminer la luminosité 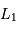 de l'étoile 1 et celle
de l'étoile 1 et celle 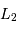 de l'autre composante en unité solaire (la magnitude absolue visuelle
de l'autre composante en unité solaire (la magnitude absolue visuelle 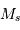 du Soleil vaut 4.8).
du Soleil vaut 4.8).
Aide [1 points]