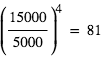Maxima
En supposant la brillance de chaque disque uniforme, dans les cas où l'éclipse est totale, la comparaison du maximum principal et du maximum secondaire de la courbe de lumière permet de déterminer le rapport des températures des deux étoiles.
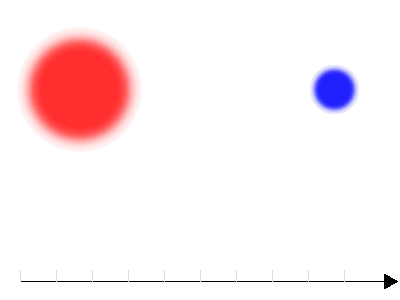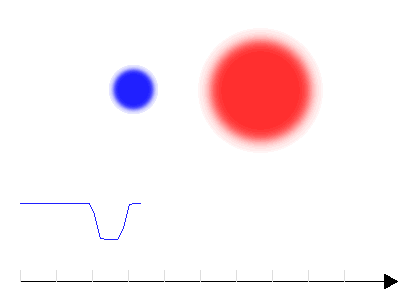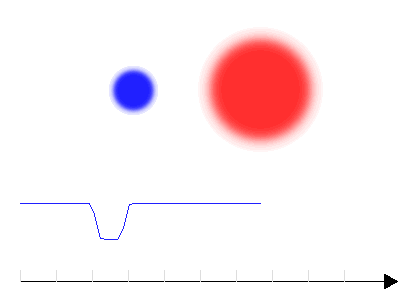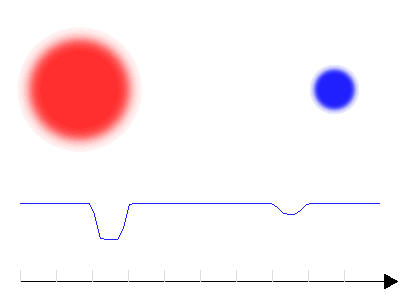
Courbe de lumière d'une binaire à éclipse avec 2 composantes présentant un fort contraste en température
Crédit :
ASM
Courbe de lumière
Lorsque le contraste en température est marqué, les minima des deux éclipses diffèrent sensiblement ; la baisse de flux est plus forte lorsque la composante chaude est occultée.
Forme des minima, températures rayons stellaires

L'allure des minima apporte des renseignements comparatifs sur les 2 composantes.
La première appliquette explicite les arguments permettant de comparer les tailles : lorsque la plus petite étoile du couple disparaît, le flux est uniformément bas.

La deuxième appliquette explicite les arguments permettant de comparer les températures : lorsque c'est l'étoile la plus chaude du couple qui disparaît, le minimum est plus profond.
 Système binaire et températures
Système binaire et températures
Difficulté : ☆
Temps : 30 min
Une des composantes d'une binaire à éclipse a une température effective de 15000 K, l'autre de 5000 K. La plus froide est une géante de rayon 4 fois plus grand que celui de la plus chaude.
Question 1)
Quel est le rapport des luminosités des deux étoiles ?
Question 2)
Quelle est l'étoile éclipsée au minimum primaire ?
Question 3)
Le minimum principal correspond-il à une éclipse totale ou à une éclipse annulaire ?
Question 4)
Quel est le rapport de profondeur entre les minima ?
 AR Lacertae : forme de la courbe de lumière
AR Lacertae : forme de la courbe de lumière
Difficulté : ☆
Temps : 30 min
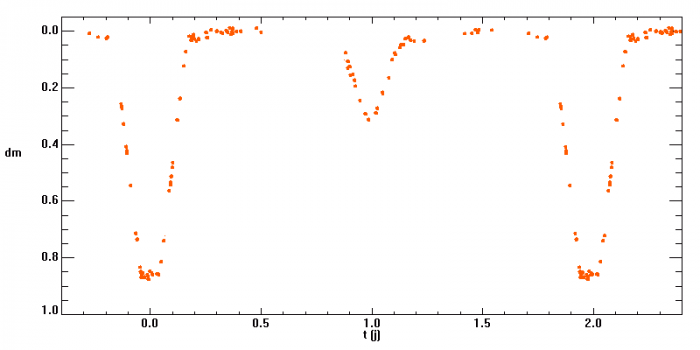
Courbe de lumière de AR Lacertae.
Crédit :
ASM
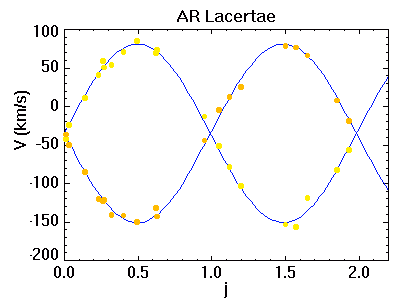
Courbe de vitesse radiale de AR Lacertae
Crédit :
ASM
On considère l'étoile double AR Lacertae, dont on a observé la courbe de lumière et les vitesses radiales des deux composantes. La période du système vaut 1.983 j.

Question 1)
Commenter la forme des deux minima. Les températures des 2 étoiles peuvent-elles être identiques ?
[3 points]
Question 2)
Justifier que l'inclinaison est proche de 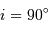 et que les orbites sont circulaires.
et que les orbites sont circulaires.
[3 points]
Question 3)
Représenter schématiquement les positions de l'étoile compagnon sur l'orbite relative en fonction des phases d'éclipse observées sur la courbe de lumière.
[2 points]
Question 4)
A l'aide de l'appliquette, estimer la durée de la phase de totalité, celle de l'éclipse principale dans son ensemble, ainsi que la profondeur (en magnitude) du minimum primaire.
[2 points]
 AR Lacertae : mesure des paramètres physiques
AR Lacertae : mesure des paramètres physiques
Difficulté : ☆
Temps : 30 min
On se propose d'analyser la courbe de lumière de AR Lacertae pour en déduire les paramètres physiques des deux composantes : rayons, températures, éclats apparents et luminosités intrinsèques...
Question 2)
Préciser laquelle des deux étoiles est la plus chaude.
[1 points]
Question 3)
Déterminer le rapport des luminosités 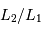 des deux étoiles. Commenter.
des deux étoiles. Commenter.
[2 points]
Question 4)
L'étude spectroscopique de l'étoile 1 indique que son type spectral est K0 et sa classe de luminosité IV (sous-géante). Sa magnitude absolue peut donc être estimée à 3. Déterminer la luminosité 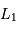 de l'étoile 1 et celle
de l'étoile 1 et celle 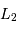 de l'autre composante en unité solaire (la magnitude absolue visuelle
de l'autre composante en unité solaire (la magnitude absolue visuelle 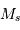 du Soleil vaut 4.8).
du Soleil vaut 4.8).
[1 points]
- Question 1
Aide :
Voir le rayonnement du corps noir
Solution :
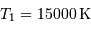 ,
, 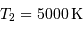 , donc
, donc 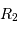 le rayon de la plus froide est égal à 4
le rayon de la plus froide est égal à 4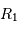 .
.
D'après la loi de rayonnement du corps noir, on a : 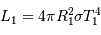 et
et 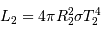 .
.
D'où :
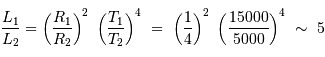
- Question 2
Aide :
voir la page loi de Stefan.
Solution :
La surface occultée est toujours égale à celle de la plus petite étoile (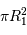 ). Conséquence de la loi de rayonnement du corps noir, le minimum principal correspond donc à l'occultation de l'étoile la plus chaude, ici en l'occurrence, la plus petite...
). Conséquence de la loi de rayonnement du corps noir, le minimum principal correspond donc à l'occultation de l'étoile la plus chaude, ici en l'occurrence, la plus petite...
- Question 3
Solution :
La plus petite étoile est occultée, il s'agit donc d'une éclipse totale
- Question 4
Aide :
Voir le paragraphe sur les mesures de température
Solution :
Le rapport des profondeurs est de 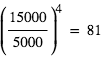
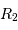 est le rayon de la plus petite étoile, les deux minima se produisent lorsque la même aire
est le rayon de la plus petite étoile, les deux minima se produisent lorsque la même aire 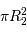 est occultée. Lorsque l'aire occultée appartient à l'étoile la plus chaude, de température
est occultée. Lorsque l'aire occultée appartient à l'étoile la plus chaude, de température 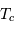 , la courbe de lumière passe par son minimum principal. De même, lorsque la surface occultée appartient à l'étoile la plus froide, de température
, la courbe de lumière passe par son minimum principal. De même, lorsque la surface occultée appartient à l'étoile la plus froide, de température 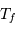 , la courbe de lumière passe par son minimum secondaire. Ainsi, si
, la courbe de lumière passe par son minimum secondaire. Ainsi, si 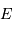 est l'éclat apparent correspondant à la phase où les deux étoiles sont visibles simultanément et sans occultation,
est l'éclat apparent correspondant à la phase où les deux étoiles sont visibles simultanément et sans occultation, 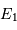 l'éclat du minimum principal et
l'éclat du minimum principal et 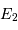 celui du minimum secondaire, on a :
celui du minimum secondaire, on a :
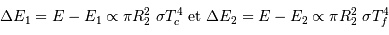
![{\Delta E_1 \over \Delta E_2} = \frac{E-E_1}{E-E_2} = \left[ \frac{T_c}{T_f}\right]^4](../pages_eclipses/equations_binaires-temperatures/equation9.png)
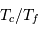 .
.




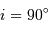 et que les orbites sont circulaires.
et que les orbites sont circulaires.
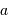 mesurant la séparation des deux étoiles,
mesurant la séparation des deux étoiles, 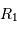 le rayon de la plus grosse,
le rayon de la plus grosse, 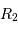 celui de la plus petite, déterminer
celui de la plus petite, déterminer 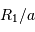 et
et 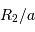 à partir de la figure.
à partir de la figure.
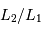 des deux étoiles. Commenter.
des deux étoiles. Commenter.
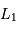 de l'étoile 1 et celle
de l'étoile 1 et celle 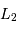 de l'autre composante en unité solaire (la magnitude absolue visuelle
de l'autre composante en unité solaire (la magnitude absolue visuelle 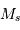 du Soleil vaut 4.8).
du Soleil vaut 4.8).
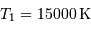 ,
, 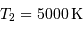 , donc
, donc 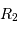 le rayon de la plus froide est égal à 4
le rayon de la plus froide est égal à 4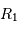 .
.
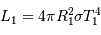 et
et 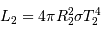 .
.
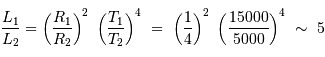
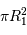 ). Conséquence de la loi de rayonnement du corps noir, le minimum principal correspond donc à l'occultation de l'étoile la plus chaude, ici en l'occurrence, la plus petite...
). Conséquence de la loi de rayonnement du corps noir, le minimum principal correspond donc à l'occultation de l'étoile la plus chaude, ici en l'occurrence, la plus petite...