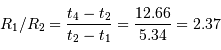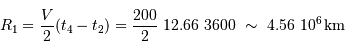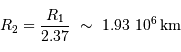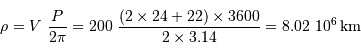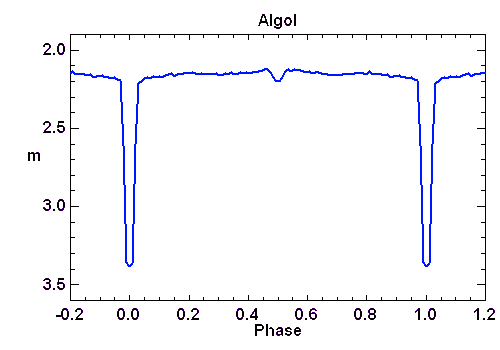
Courbe de lumière d'Algol.
Crédit :
ASM
La courbe de lumière d'Algol
Algol, dont le nom vient de l'arabe Al Guhl esprit changeant est l'étoile 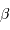 de la constellation de Persée (
de la constellation de Persée (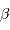 Persei). Son comportement est connu depuis plusieurs siècles car ses variations d'éclat sont spectaculaires et particulièrement visibles à l'oeil nu.
Persei). Son comportement est connu depuis plusieurs siècles car ses variations d'éclat sont spectaculaires et particulièrement visibles à l'oeil nu.
Sa luminosité totale diminue en effet en quelques heures jusqu'au tiers de sa valeur habituelle, puis remonte pour rester quasiment stable pendant deux jours et demi. Puis le cycle recommence... Algol est un couple de binaires à éclipse, dont la plus brillante est de type spectral B (blanc bleuté), et la plus faible est de type K (jaune orangé).
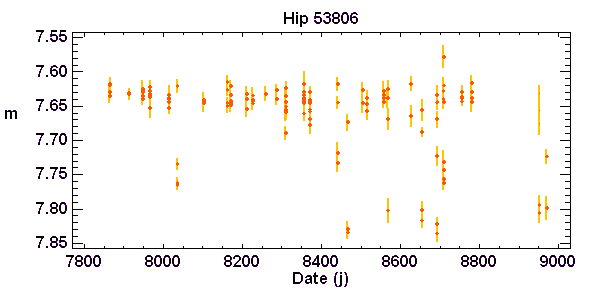
Magnitude d'une binaire à éclipse de type Algol en fonction du temps. Observations du satellite européen Hipparcos
Crédit :
Hipparcos/ASM
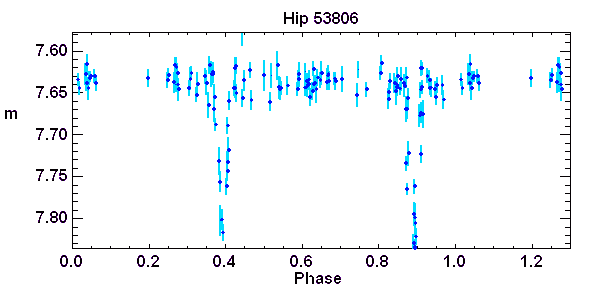
Courbe de lumière d'une binaire à éclipse de type Algol. Observations du satellite européen Hipparcos
Crédit :
Hipparcos/ASM
Binaires à éclipse de type Algol
Les observations de la courbe de lumière donne la magnitude totale du système en fonction du temps. La périodicité de la série temporelle est analysée, pour conduire à la courbe de lumière en fonction de la phase.
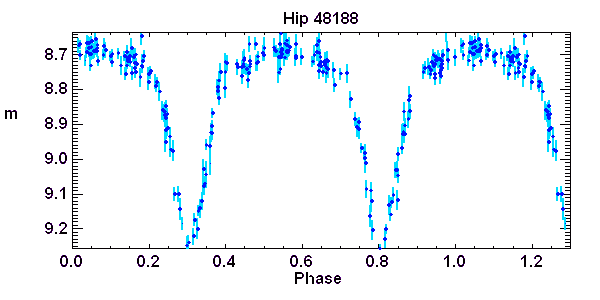
Courbe de lumière d'une étoile de type Beta Lyrae. Observations du satellite européen Hipparcos
Crédit :
Hipparcos/ASM
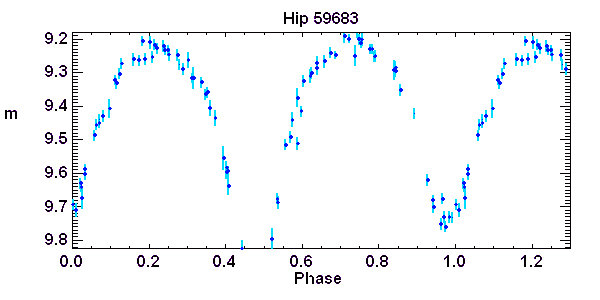
Courbe de lumière d'une étoile de type W Ursae. Observations du satellite européen Hipparcos
Crédit :
Hipparcos/ASM
Binaires à éclipse serrées
classes de binaires correspondent à des couples très serrées, présentant alors des périodes très courtes, bien plus rapides que le type Algol, telles les variables de type Beta Lyrae ou
W Ursae Majoris. Ces dernières, moins massives, sont le plus souvent tellement proches l'une de l'autre qu'elles remplissent leur lobe de Roche, et échangent de la matière.

Image du disque solaire en lumière visible montrant l'assombrissement du disque dans les régions proches du limbe.
Crédit :
ASM
Assombrissement centre bord
Le profil des courbes de lumière, arrondi, dévoile que les étoiles ne sont pas des disques de brillance uniforme. En effet, comme pour le Soleil, les régions visibles proches du limbe sont sondées à des altitudes plus élevées, où la température est plus froide.
Courbe de lumière
Les variations de la magnitude en fonction du temps donnent la courbe de lumière. L'étude de la forme de cette courbe permet en principe de reconstituer les paramètres de l'orbite. On notera cependant que ces couples d'étoiles étant serrés, la courbe de lumière peut parfois être déformée par les interactions entre les deux composantes : par exemple des effets de réflexion de lumière entre les deux étoiles ou des déformations des étoiles elles-mêmes qui, sous l'effet des forces de marées, ne sont plus sphériques.
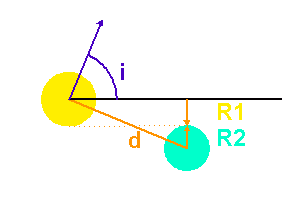
Paramètres de l'éclipse.
Crédit :
ASM
Occultation
L'occultation sera partielle ou totale selon les diamètres relatifs des étoiles et l'inclinaison du plan de l'orbite par rapport à la ligne de visée : il y a en effet éclipse (partielle ou totale) lorsque la distance 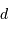 entre les étoiles est telle que
entre les étoiles est telle que
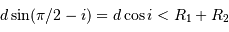
où 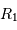 et
et 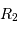 sont les rayons de chaque étoile.
sont les rayons de chaque étoile.
Dans le cas où 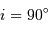 , les deux éclipses sont centrales, l'une étant totale (quand la plus grosse passe devant la plus petite), l'autre étant annulaire. On remarquera par ailleurs que lorsqu'il y a éclipse totale les minima de la courbe de lumière montrent un plateau, qui correspond à la durée effective de totalité de l'éclipse ou de l'occultation.
, les deux éclipses sont centrales, l'une étant totale (quand la plus grosse passe devant la plus petite), l'autre étant annulaire. On remarquera par ailleurs que lorsqu'il y a éclipse totale les minima de la courbe de lumière montrent un plateau, qui correspond à la durée effective de totalité de l'éclipse ou de l'occultation.
Orbite circulaire
On reconnaît que l'orbite est circulaire quand les deux éclipses se produisent exactement toutes les demi-périodes. Dans ce cas, il est alors possible de déterminer l'inclinaison et les rayons relatifs des étoiles 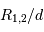 .
.
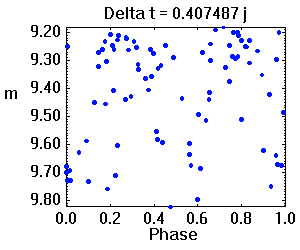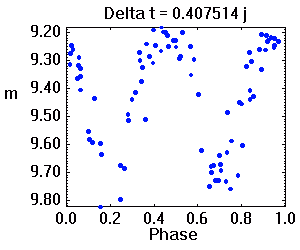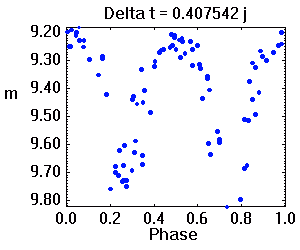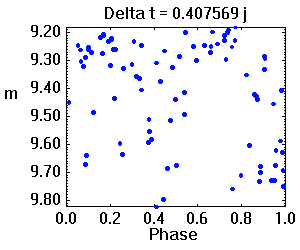
Tracé de la courbe de lumière repliée sur diverses périodes. La période adéquate assure une moindre dispersion des valeurs.
Crédit :
ASM
De la série temporelle à la phase
L'animation ci-jointe montre l'évolution de la série temporelle à la phase orbitale, par balayage de la période. La période adéquate est celle qui assure une moindre dispersion des valeurs.

Courbe de lumière d'une binaire à éclipse de type Algol.
Crédit :
ASM
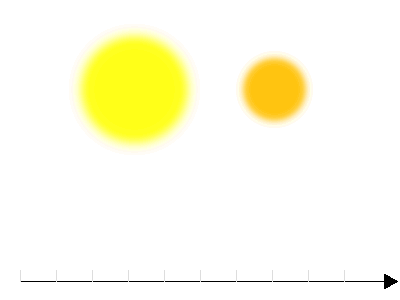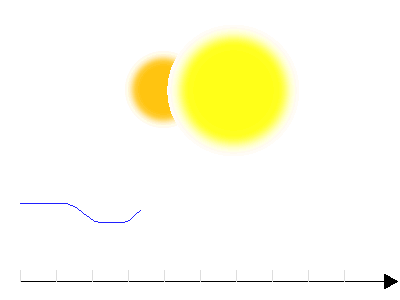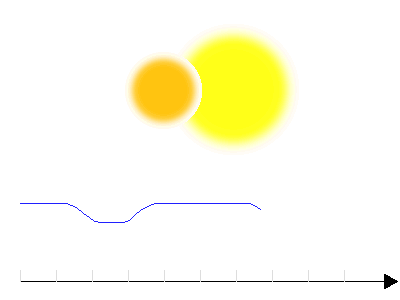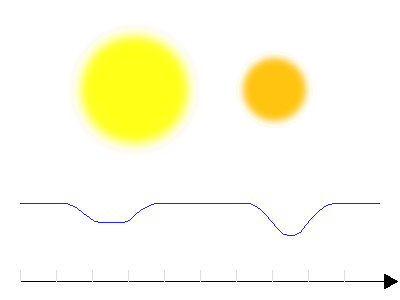
Courbe de lumière d'une binaire à éclipse de type W Ursae Majoris
Crédit :
ASM
Courbe de lumière
Les binaires de type Algol sont nettement séparées, alors que celles de type W Ursae Majoris sont très proches. Les membres d'un couple W Ursae Majoris présentent un profil déformé par le champ gravitationnel du compagnon ; la courbe de lumière présente des formes très arrondies.
 Système binaire et courbe de lumière
Système binaire et courbe de lumière
Difficulté : ☆
Temps : 30 min

Courbe de lumière schématique : variation de l'éclat en fonction du temps.
Crédit :
ASM
On observe un système binaire à éclipse 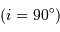 dont les orbites sont circulaires. La courbe de lumière correspond à la figure ci-dessus. Soient
dont les orbites sont circulaires. La courbe de lumière correspond à la figure ci-dessus. Soient 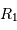 et
et 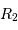 les rayons des deux étoiles,
les rayons des deux étoiles, 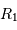 étant le rayon de la plus grosse. On notera
étant le rayon de la plus grosse. On notera 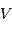 la vitesse relative du mouvement orbital de la plus petite par rapport à la plus grosse.
la vitesse relative du mouvement orbital de la plus petite par rapport à la plus grosse.
Question 2)
La période P du mouvement orbital est de 2 jours et 22 heures. La durée de chaque éclipse est par ailleurs de 18h00min, et la totalité dure 7h19min. En déduire le rapport des rayons 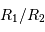 .
.
Question 4)
Montrer que, d'après la figure, l'étoile la plus chaude est la plus petite.
A quoi correspond le minimum arrondi ?
 Durée d'une éclipse
Durée d'une éclipse
Difficulté : ☆☆
Temps : 30 min
Cet exercice s'intéresse à mesurer la durée d'une éclipse dans un système stellaire binaire. Pour simplifier, on suppose l'orbite circulaire. Les observables sont : la période orbitale 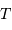 et la durée du transit
et la durée du transit 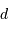 .
.
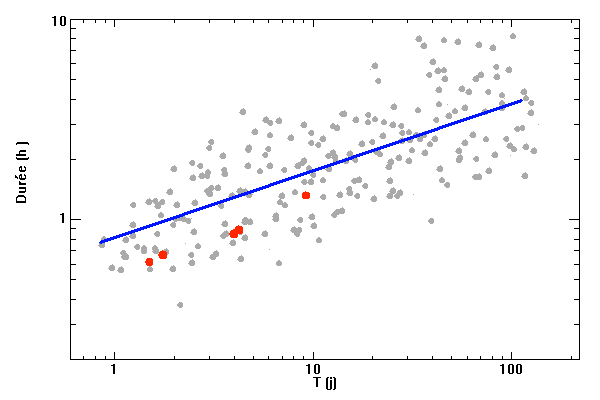
Durée d'un transit, fonction de la période orbitale du système double. Les points gris rapportent des événements de binaires à éclipses. Les points rouges rapportent des transits exoplanétaires observés par CoRoT.
Crédit :
ASM
Question 1)
Montrer que la durée d'un transit est inversement proportionnelle à la vitesse orbitale.
[1 points]
On fera l'hypothèse que les étoiles ont un rayon moyen voisin du rayon solaire.
Question 2)
Montrer que la durée 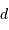 d'un transit varie comme
d'un transit varie comme 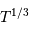 .
.
[1 points]
S'intéresser à la vitesse orbitale.
Question 3)
Expliquer la dispersion des points sur la courbe jointe.
[1 points]
S'intéresser aux rayons stellaires.
Question 4)
Pourquoi les planètes découvertes par CoRoT ont-elles des durées de transit légèrement inférieures ?
[1 points]
Comparer les tailles des objets.
- Question 1
Aide :
Ecrire une relation entre 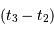 ,
, 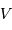 ,
, 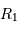 et
et 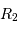 ; puis entre
; puis entre 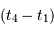 ,
, 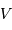 ,
, 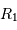 et
et 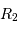 .
.
Solution :
Le trajet de la petite étoile pour aller de la position 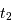 à la position
à la position 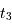 est égal à
est égal à 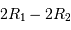 . De la même façon, le trajet de la petite étoile pour aller de la position
. De la même façon, le trajet de la petite étoile pour aller de la position 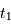 à la position
à la position 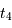 est égal à
est égal à 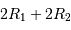 . Si l'on assimile la corde de l'arc de cercle de la trajectoire à une droite, ce qui revient à dire que l'orbite est grande vis à vis des rayons des étoiles, on obtient :
. Si l'on assimile la corde de l'arc de cercle de la trajectoire à une droite, ce qui revient à dire que l'orbite est grande vis à vis des rayons des étoiles, on obtient :
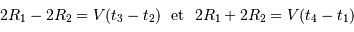
D'où 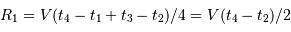 et
et 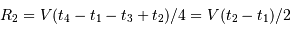
- Question 2
Solution :
On a 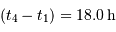 et
et 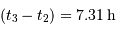 , d'où
, d'où 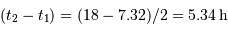 et
et 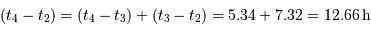 et donc, d'après le résultat de la question précédente :
et donc, d'après le résultat de la question précédente :
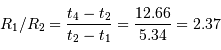
- Question 3
Solution :
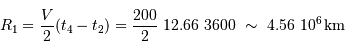
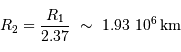
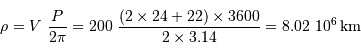
- Question 4
Aide :
A quoi correspond le minimum arrondi ?
Aide :
Voir la loi de rayonnement du corps noir.
Solution :
La même aire est occultée à chaque éclipse, que la petite étoile passe devant ou derrière la plus grosse.
En vertu de la loi de rayonnement du corps noir, c'est lorsque l'étoile la plus chaude est occultée que le minimum est le plus profond.
C'est lorsque la plus petite étoile est éclipsée que le fond du minimum est plat durant un certain laps de temps ; lorsque la plus grande est éclipsée, l'assombrissement du centre au bord arrondit la courbe de lumière. Ici, c'est donc la plus petite étoile qui est la plus chaude.

 de la constellation de Persée (
de la constellation de Persée ( Persei). Son comportement est connu depuis plusieurs siècles car ses variations d'éclat sont spectaculaires et particulièrement visibles à l'oeil nu.
Persei). Son comportement est connu depuis plusieurs siècles car ses variations d'éclat sont spectaculaires et particulièrement visibles à l'oeil nu.






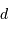 entre les étoiles est telle que
entre les étoiles est telle que
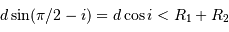
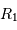 et
et 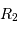 sont les rayons de chaque étoile.
sont les rayons de chaque étoile.
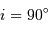 , les deux éclipses sont centrales, l'une étant totale (quand la plus grosse passe devant la plus petite), l'autre étant annulaire. On remarquera par ailleurs que lorsqu'il y a éclipse totale les minima de la courbe de lumière montrent un plateau, qui correspond à la durée effective de totalité de l'éclipse ou de l'occultation.
, les deux éclipses sont centrales, l'une étant totale (quand la plus grosse passe devant la plus petite), l'autre étant annulaire. On remarquera par ailleurs que lorsqu'il y a éclipse totale les minima de la courbe de lumière montrent un plateau, qui correspond à la durée effective de totalité de l'éclipse ou de l'occultation.
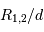 .
.




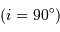 dont les orbites sont circulaires. La courbe de lumière correspond à la figure ci-dessus. Soient
dont les orbites sont circulaires. La courbe de lumière correspond à la figure ci-dessus. Soient 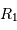 et
et 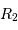 les rayons des deux étoiles,
les rayons des deux étoiles, 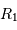 étant le rayon de la plus grosse. On notera
étant le rayon de la plus grosse. On notera 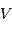 la vitesse relative du mouvement orbital de la plus petite par rapport à la plus grosse.
la vitesse relative du mouvement orbital de la plus petite par rapport à la plus grosse.
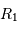 et
et 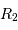 en fonction des dates
en fonction des dates 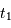 ,
, 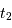 ,
, 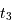 et
et 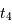 et de la vitesse relative des deux étoiles.
et de la vitesse relative des deux étoiles.
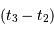 ,
, 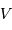 ,
, 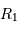 et
et 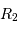 ; puis entre
; puis entre 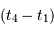 ,
, 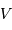 ,
, 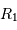 et
et 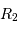 .
.
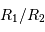 .
.
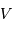 est de 200 km/s. Calculer
est de 200 km/s. Calculer 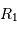 ,
, 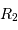 et la distance
et la distance 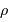 entre les deux étoiles.
entre les deux étoiles.
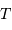 et la durée du transit
et la durée du transit 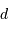 .
.

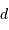 d'un transit varie comme
d'un transit varie comme 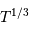 .
.
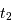 à la position
à la position 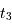 est égal à
est égal à 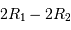 . De la même façon, le trajet de la petite étoile pour aller de la position
. De la même façon, le trajet de la petite étoile pour aller de la position 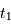 à la position
à la position 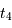 est égal à
est égal à 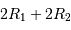 . Si l'on assimile la corde de l'arc de cercle de la trajectoire à une droite, ce qui revient à dire que l'orbite est grande vis à vis des rayons des étoiles, on obtient :
. Si l'on assimile la corde de l'arc de cercle de la trajectoire à une droite, ce qui revient à dire que l'orbite est grande vis à vis des rayons des étoiles, on obtient :
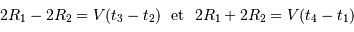
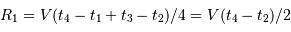 et
et 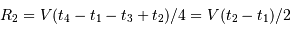
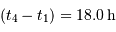 et
et 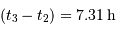 , d'où
, d'où 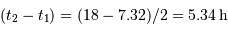 et
et 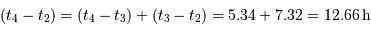 et donc, d'après le résultat de la question précédente :
et donc, d'après le résultat de la question précédente :