
La surface de Io, recouverte de volcans géants et de dépôts de soufre.
Crédit :
NASA
Le volcanisme sur Io
Io, satellite de Jupiter, possède pratiquement les mêmes masse, diamètre et rayon orbital que la Lune. Sa surface est couverte de volcans (actifs et inactifs) et de lacs de lave. L'activité volcanique est telle que les dépôts volcaniques s'accumulent au rythme d'environ 1 mm d'épaisseur par année sur toute la surface d'Io. De tous les objets du système solaire, Io est celui dont la surface se renouvelle le plus rapidement.
D'où vient l'énergie dissipée par le volcanisme ?
Les volcans d'Io expulsent du gaz à plus de 1 km/s, 20 fois plus vite que ne le fait un volcan terrestre. Ce volcanisme d'Io puise sa source dans l'effet de marée. A cause de la proximité de Io et de la masse de la planète, Jupiter étant 318 fois plus massif que la Terre, les renflements de marée que subit le satellite ont une amplitude de plusieurs kilomètres.
Si, comme la Lune, Io a ses périodes de rotation et de révolution
synchronisées, son mouvement est de plus fortement perturbé par 2 autres lunes de Jupiter, Europe et Ganymède, avec lesquels son orbite est résonante.
Sous l'effet de
l'attraction des autres satellites, Io est tantôt
en avance, tantôt en retard par rapport à sa révolution moyenne, ce qui
a pour effet de déplacer le bourrelet de marée, et conduit à une forte dissipation d'énergie :
la variabilité et le déplacement des renflements de marée dégradent par friction suffisamment d'énergie pour faire fondre partiellement l'intérieur du satellite et engendrer ainsi une activité volcanique.
Forces de marée de la Terre sur la Lune
La Terre étant 81 fois plus massive que la Lune, l'effet de marée de la Terre sur la Lune est important : cette marée a synchronisé la rotation propre de la lune et sa révolution autour de la Terre. C'est pour cette raison que nous voyons toujours la même face de la Lune.
Sous l'action du champ de marée terrestre, la Lune a été déformée et le bourrelet de déformation est en moyenne aligné dans l'axe Terre-Lune.
Rotation synchrone
Si la Lune ne tournait pas autour de la Terre de façon à présenter toujours la même face, ce bourrelet se déplacerait et créerait des frottements. La période de rotation propre de la Lune a diminué, et s'est ajustée à celle de révolution autour de la Terre, de telle façon que la Lune présente toujours la même face à la Terre. Ces frottements sont nuls lorsque le bourrelet ne se déplace plus.
 Remarque
Remarque
Ce qui est vrai pour la Lune est aussi vrai pour la Terre : les effets de la marée lunaire continuent de freiner la rotation de la Terre. La journée s'allonge de 2 microsecondes par an.
A l'instar de la Lune, tous les gros satellites du système solaire présentent une rotation synchrone avec celle de leur planète.

Animation montrant la rotation synchrone. L'égalité des périodes de révolution et de rotation conduit le satellite à toujours présenter la même face à sa planète. La rotation de la Terre est indiquée par le rayon vecteur rouge.
Crédit :
ASM
Rotation synchrone
Animation montrant la rotation synchrone. La lune présente ainsi toujours la même face à la Terre
Animation montrant la libration. Les périodes de libration et de révolution sont très voisines.
Crédit :
ASM
Libration et nutation
Animation montrant comment la libration modifie légèrement la rotation synchrone. La libration mesure l'oscillation de la Lune autour de sa position moyenne.
 Sphère d'influence
Sphère d'influence
Difficulté : ☆☆
Temps : 30 min
La sphère d'influence d'une planète de masse 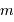 orbitant sur une orbite circulaire de rayon
orbitant sur une orbite circulaire de rayon 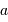 autour de son étoile de masse
autour de son étoile de masse 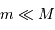 peut-être définie comme la zone à l'intérieur de laquelle un satellite reste piégé autour de la planète (à l'extérieur de cette sphère, le satellite est capturé en orbite autour de l'étoile). Pour déterminer le rayon de cette sphère, on cherche dans le référentiel tournant avec la planète la position d'équilibre entre les 2 corps
peut-être définie comme la zone à l'intérieur de laquelle un satellite reste piégé autour de la planète (à l'extérieur de cette sphère, le satellite est capturé en orbite autour de l'étoile). Pour déterminer le rayon de cette sphère, on cherche dans le référentiel tournant avec la planète la position d'équilibre entre les 2 corps 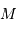 et
et 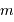 . On note
. On note 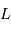 cette position (1er point de Lagrange).
cette position (1er point de Lagrange).
Question 2)
Montrer, en identifiant les différents termes, que la relation suivante définit l'état d'équilibre du satellite dans le référentiel
barycentrique :
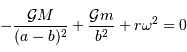
[3 points]
Identifier les champs gravitationnels et le terme lié au référentiel tournant.
Faire un schéma.
Ecrire le principe fondamental de la dynamique dans le référentiel barycentrique.
Question 3)
Développer cette relation en ne retenant que les termes d'ordre 0 ou 1 (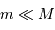 et
et 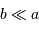 ). En déduire que :
). En déduire que :
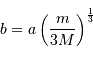
[3 points]



 orbitant sur une orbite circulaire de rayon
orbitant sur une orbite circulaire de rayon 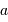 autour de son étoile de masse
autour de son étoile de masse 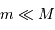 peut-être définie comme la zone à l'intérieur de laquelle un satellite reste piégé autour de la planète (à l'extérieur de cette sphère, le satellite est capturé en orbite autour de l'étoile). Pour déterminer le rayon de cette sphère, on cherche dans le référentiel tournant avec la planète la position d'équilibre entre les 2 corps
peut-être définie comme la zone à l'intérieur de laquelle un satellite reste piégé autour de la planète (à l'extérieur de cette sphère, le satellite est capturé en orbite autour de l'étoile). Pour déterminer le rayon de cette sphère, on cherche dans le référentiel tournant avec la planète la position d'équilibre entre les 2 corps 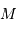 et
et 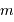 . On note
. On note 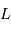 cette position (1er point de Lagrange).
cette position (1er point de Lagrange).
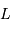 à la planète étant notée
à la planète étant notée 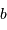 , déterminer les distances de
, déterminer les distances de 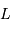 à l'étoile et de
à l'étoile et de 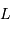 au barycentre
au barycentre 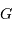 du système (planète-étoile) en fonction de
du système (planète-étoile) en fonction de 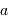 et
et 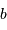 . On note
. On note 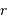 cette dernière distance.
cette dernière distance.
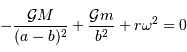
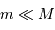 et
et  ). En déduire que :
). En déduire que :
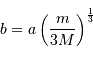
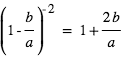 dans le terme d'interaction gravitationnelle et négliger
dans le terme d'interaction gravitationnelle et négliger 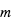 devant
devant 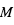 dans le terme de rotation.
dans le terme de rotation.
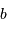 pour la Terre (
pour la Terre (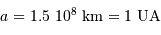 ) et
comparer à la distance Terre-Lune (380 000 km). Calculer
) et
comparer à la distance Terre-Lune (380 000 km). Calculer 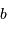 pour le
Soleil qui orbite autour du centre
galactique (
pour le
Soleil qui orbite autour du centre
galactique (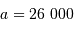 années de lumière, masse
années de lumière, masse 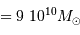 ), et comparer à la
distance moyenne entre deux étoiles (distance Soleil-Proxima du
Centaure = 4.2 AL), ainsi qu'à la distance du
nuage de Oort
(de l'ordre de
), et comparer à la
distance moyenne entre deux étoiles (distance Soleil-Proxima du
Centaure = 4.2 AL), ainsi qu'à la distance du
nuage de Oort
(de l'ordre de 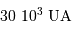 ).
).
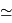 63 000 UA.
63 000 UA.