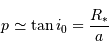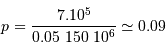Fraction d'un champ stellaire observée par le satellite CoRoT. Au total, plusieurs milliers de cibles sont suivies simultanément.
Crédit :
CoRoT/CNES
Détecter et identifier un transit nécessite une grande précision photométrique, telle que l'apporte CoRoT, la première mission dédiée à ce thème de recherche.
Crédit :
CoRoT/CNES
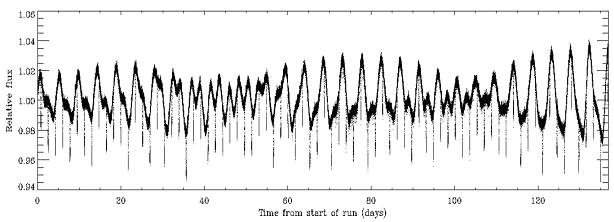
Les transits, ici événements très fins de profondeur relative 4%, se superposent à un flux stellaire éminemment variable.
Crédit :
CoRoT/CNES
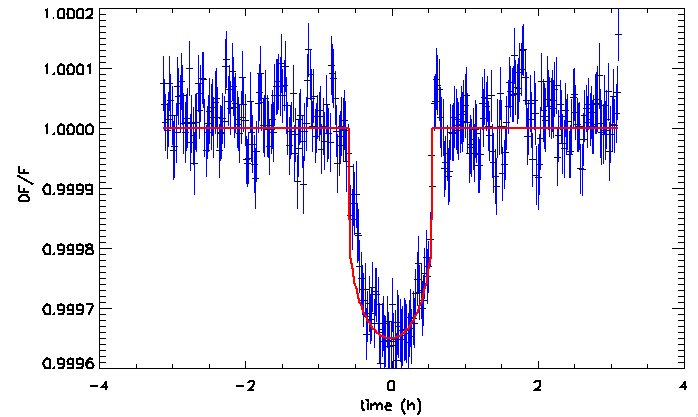
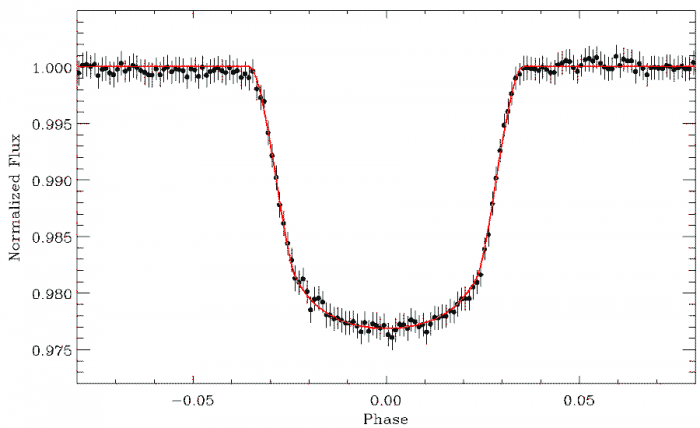
Transit profond de seulement 0.4% observé par CoRoT (planète CoRoT-Exo-7b, de rayon égal à 1.8 fois celui de la Terre).
Crédit :
CoRoT/CNES
Observer beaucoup d'étoiles
La probabilité de détection d'une planète étant faible, un programme de détection par transits doit nécessairement suivre simultanément un
grand nombre de cibles, ce que permet la photométrie.
Observer longtemps
Un transit seul n'apporte pas d'information, et peut être confondu avec un événement non planétaire. Les séquences d'observation de CoRoT durent 5 mois, et la répétition de trois événements est attendue.
Observer précisément
Distinguer un transit planétaire des multiples autres sources possibles de
variation du flux stellaire n'est pas toujours simple.
Les planètes les moins massives détectées, par transit et donc sans l'ambiguïté du facteur de projection 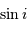 , ont été observées par le satellite CoRoT puis Kepler.
, ont été observées par le satellite CoRoT puis Kepler.
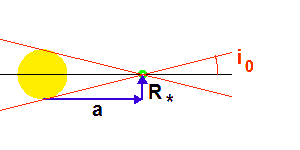
Le rayon planétaire étant négligé devant le rayon stellaire, l'angle séparant le plan orbital de l'axe de visée doit être inférieur à une valeur limite pour qu'il y ait occultation.
Crédit :
ASM
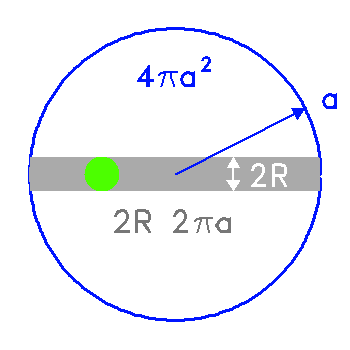
La probabilité de transit
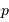
est obtenue par le rapport de l'aire balayée par la planète à l'aire de la sphère de rayon égal au demi-grand axe planétaire :
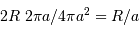
.
Crédit :
ASM
Précision photométrique
Le deuxième facteur limitant est photométrique. En effet, depuis le sol il est difficile d'obtenir une précision photométrique meilleure que 1 % (c'est-à-dire 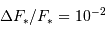 ) en raison de l'agitation atmosphérique. Les observations depuis l'espace, en revanche, permettent d'atteindre une précision aussi bonne que
) en raison de l'agitation atmosphérique. Les observations depuis l'espace, en revanche, permettent d'atteindre une précision aussi bonne que 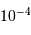 , et donc de détecter des planètes de type tellurique.
, et donc de détecter des planètes de type tellurique.
Limite de détection par la méthode des transits
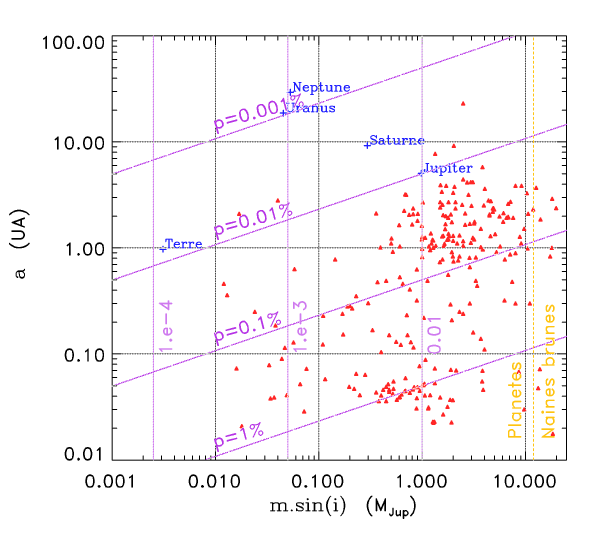
La détection des planètes les moins massives nécessite une
excellente précision photométrique. La probabilité de détection
décroît fortement avec l'évolution du demi-grand axe.
Crédit :
ASM
Observation de transits
Il s'ensuit que, pour être efficace, les projets de détection
d'exoplanètes par transit doivent observer un très grand nombre de
cibles, avec la meilleure précision
photométrique possible. De plus, pour éviter tout effet
stroboscopique, il faut observer continûment. L'espace est l'endroit idéal pour ceci, comme l’ont démontré les mission CoRoT et Kepler.
Confirmation des observations
Plusieurs artefacts observationnels peuvent imiter la signature
d'un transit planétaire. Les plus courants sont l'observation d'un
système stellaire double, ou d'une binaire à éclipses présente
dans le champ d'observation de l'étoile principale. Dans ces deux
cas, la baisse de flux peut être faible et confondue avec celle
d'une hypothétique planète. Une vérification a posteriori s'impose
pour déterminer les éventuels faux positifs, menée le plus souvent
en vélocimétrie Doppler, et parfois par imagerie en optique adaptative.
 Limitation de la méthode du transit
Limitation de la méthode du transit
Difficulté : ☆☆
Temps : 30 min
Avant les missions spatiales CoRoT et Kepler, peu de transits avaient été observés ; leur nombre a ensuite explosé. L'exercice se propose de déterminer la probabilité 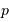 d'un tel événement, fonction du rayon de l'étoile
d'un tel événement, fonction du rayon de l'étoile 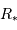 et du rayon orbital de la planète
et du rayon orbital de la planète 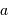 , et d'établir
, et d'établir
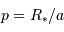 .
.

Crédit :
ASM
Question 1)
L'angle  de visée est défini comme l'angle entre la normale au plan de révolution de l'orbite et la ligne de visée.
Exprimer l'angle maximum
de visée est défini comme l'angle entre la normale au plan de révolution de l'orbite et la ligne de visée.
Exprimer l'angle maximum 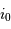 pour lequel une éclipse peut être observée, en fonction de
pour lequel une éclipse peut être observée, en fonction de 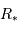 et
et 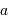 , en supposant le rayon planétaire négligeable.
, en supposant le rayon planétaire négligeable.
Faire un schéma, basé sur la figure de l'énoncé.
Question 2)
En vous aidant des propriétés de symétrie du système, déterminer de quelle(s) variable(s) dépend 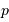 .
.
Question 3)
La probabilité 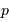 de détecter un transit est égale à la probabilité que la ligne de visée ne se trouve pas dans le demi-cône d'axe perpendiculaire au plan de l'orbite et de demi-angle au sommet
de détecter un transit est égale à la probabilité que la ligne de visée ne se trouve pas dans le demi-cône d'axe perpendiculaire au plan de l'orbite et de demi-angle au sommet 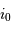 .
Calculer la mesure de l'angle solide d'un hémisphère et d'un cône de demi-angle au sommet
.
Calculer la mesure de l'angle solide d'un hémisphère et d'un cône de demi-angle au sommet 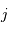 .
.
Définition de la mesure d'un angle solide (unité stéradian):
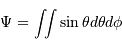
avec 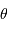 et
et 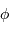 les angles d'Euler.
les angles d'Euler.
Dans le cas étudié, il y a symétrie de révolution autour de l'axe de
révolution du système.
Question 4)
Exprimer 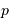 en fonction de
en fonction de 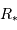 et
et 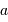 .
.
La probabilité 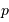 mesure la non-appartenance au cône précédemment
défini.
mesure la non-appartenance au cône précédemment
défini.
Question 5)
Application numérique pour le cas l'exoplanète 51 Peg.
Données : 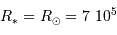 km, et
km, et 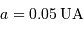 .
.
- Question 1
Aide :
Faire un schéma, basé sur la figure de l'énoncé.
Solution :
Le triangle étoile-diamètre planétaire permet d'écrire, le rayon de la planète étant supposé très petit :
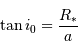
- Question 2
Solution :
Le problème est à symétrie de révolution. La position de la ligne de visée autour de l'étoile ne joue aucun rôle, la seule variable pertinente est l'angle  .
.
- Question 3
Aide :
Définition de la mesure d'un angle solide (unité stéradian):
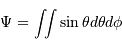
avec 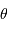 et
et 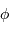 les angles d'Euler.
les angles d'Euler.
Dans le cas étudié, il y a symétrie de révolution autour de l'axe de
révolution du système.
Solution :
Mesure de l'angle solide d'un hémisphère :
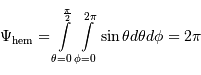
Mesure de l'angle solide d'un cône de demi-angle au sommet 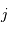 :
:
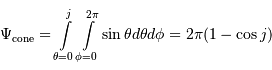
- Question 4
Aide :
La probabilité 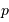 mesure la non-appartenance au cône précédemment
défini.
mesure la non-appartenance au cône précédemment
défini.
Solution :
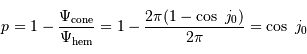
Les angles 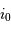 et
et 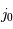 sont complémentaires :
sont complémentaires : 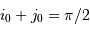 . On en tire :
. On en tire :
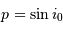
Comme de plus le rayon stellaire est petit devant le rayon de la trajectoire de l'exoplanète, l'angle 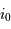 est petit, et l'on peut le confondre avec son sinus ou sa tangente.
est petit, et l'on peut le confondre avec son sinus ou sa tangente.
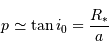
- Question 5
Solution :
Application numérique directe :
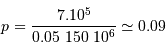




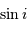 , ont été observées par le satellite CoRoT puis Kepler.
, ont été observées par le satellite CoRoT puis Kepler.


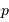 est obtenue par le rapport de l'aire balayée par la planète à l'aire de la sphère de rayon égal au demi-grand axe planétaire :
est obtenue par le rapport de l'aire balayée par la planète à l'aire de la sphère de rayon égal au demi-grand axe planétaire : 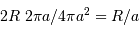 .
.
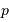 d'un tel événement vaut
d'un tel événement vaut 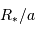 ,
, 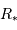 étant le rayon stellaire, et
étant le rayon stellaire, et 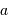 le demi-grand axe de l'orbite planétaire. Ce résultat est démontré par un calcul complet en
le demi-grand axe de l'orbite planétaire. Ce résultat est démontré par un calcul complet en 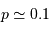 pour
pour 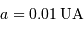 , c'est-à-dire pour les planètes détectées à ce jour qui sont sur les orbites les plus serrées. Cette probabilité décroît avec l'augmentation du demi-grand axe.
, c'est-à-dire pour les planètes détectées à ce jour qui sont sur les orbites les plus serrées. Cette probabilité décroît avec l'augmentation du demi-grand axe.
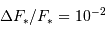 ) en raison de l'
) en raison de l'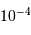 , et donc de détecter des planètes de type
, et donc de détecter des planètes de type 
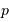 d'un tel événement, fonction du rayon de l'étoile
d'un tel événement, fonction du rayon de l'étoile 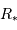 et du rayon orbital de la planète
et du rayon orbital de la planète 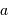 , et d'établir
, et d'établir 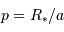 .
. de visée est défini comme l'angle entre la normale au plan de révolution de l'orbite et la ligne de visée.
Exprimer l'angle maximum
de visée est défini comme l'angle entre la normale au plan de révolution de l'orbite et la ligne de visée.
Exprimer l'angle maximum 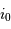 pour lequel une éclipse peut être observée, en fonction de
pour lequel une éclipse peut être observée, en fonction de 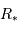 et
et 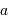 , en supposant le rayon planétaire négligeable.
, en supposant le rayon planétaire négligeable.
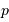 .
.
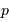 de détecter un transit est égale à la probabilité que la ligne de visée ne se trouve pas dans le demi-cône d'axe perpendiculaire au plan de l'orbite et de demi-angle au sommet
de détecter un transit est égale à la probabilité que la ligne de visée ne se trouve pas dans le demi-cône d'axe perpendiculaire au plan de l'orbite et de demi-angle au sommet 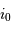 .
Calculer la mesure de l'angle solide d'un hémisphère et d'un cône de demi-angle au sommet
.
Calculer la mesure de l'angle solide d'un hémisphère et d'un cône de demi-angle au sommet 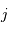 .
.
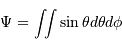
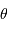 et
et 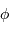 les angles d'Euler.
les angles d'Euler.
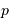 en fonction de
en fonction de 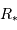 et
et 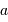 .
.
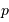 mesure la non-appartenance au cône précédemment
défini.
mesure la non-appartenance au cône précédemment
défini.
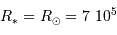 km, et
km, et 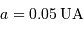 .
.
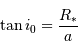
 .
.
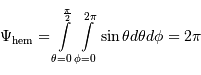
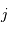 :
:
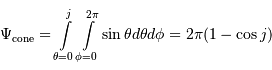
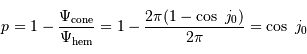
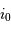 et
et 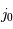 sont complémentaires :
sont complémentaires : 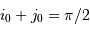 . On en tire :
. On en tire :
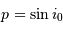
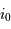 est petit, et l'on peut le confondre avec son sinus ou sa tangente.
est petit, et l'on peut le confondre avec son sinus ou sa tangente.