Détection par transit
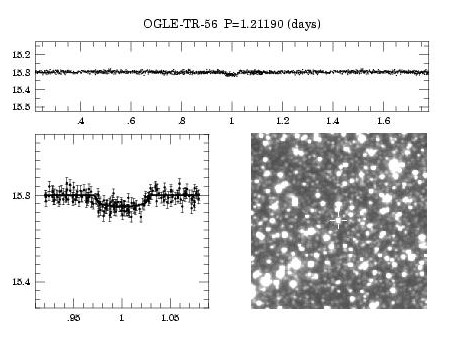
Occultation détectée par la campagne d'observation OGLE (Optical Gravitational Lensing Experiment ; Warsaw Telescope (1.3 m) installé à l'Observatoire de Las Campanas au Chili). L'aperçu de la courbe de lumière, et le zoom autour du transit montre combien la signature de ce dernier est ténue. Le champ stellaire localise la cible, de faible magnitude (V = 16).
Le temps est donné en unité de la période orbitale.
Crédit :
OGLE
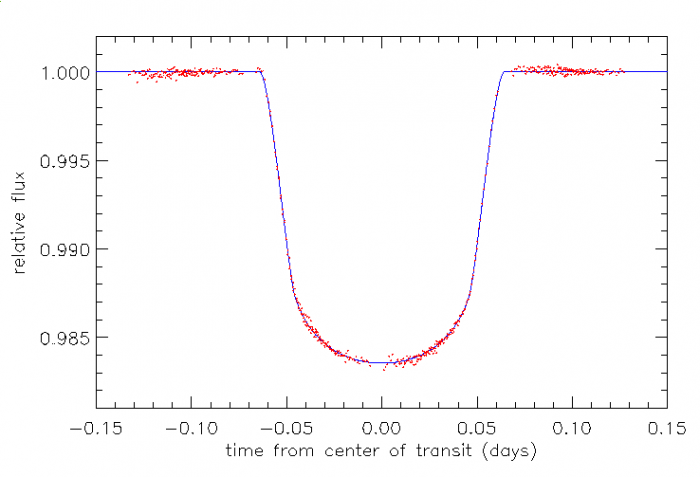
Occultation de
HD209458 par sa planète, vue par le télescope spatial Hubble. Le profil d'assombrissement du centre au bord de l'étoile occasionne la concavité du fond du transit.
Crédit :
HST
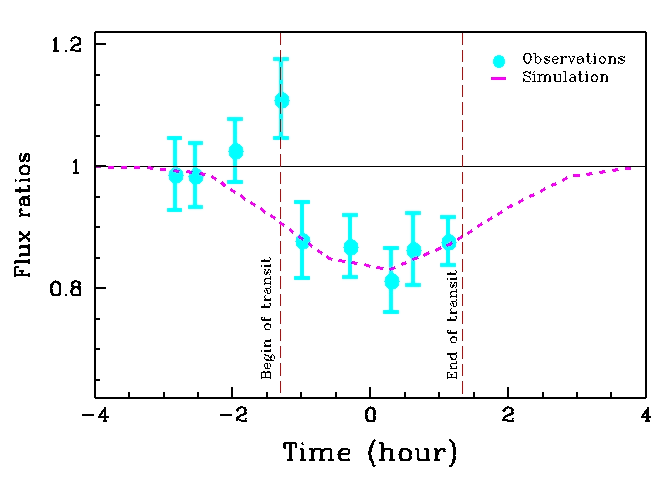
Occultation de HD209458 par sa planète, vue dans le filtre étroit de la raie Lyman alpha de l'hydrogène. L'augmentation du flux est due à la composante planétaire, et dénote vraisemblablement une atmosphère planétaire étendue.
Crédit :
HST
Transit
Le passage répété d'une planète devant son étoile provoque une diminution périodique de la luminosité de l'étoile. La forme de la figure de transit dépend du diamètre relatif de la
planète par rapport à celui de l'étoile, de l'inclinaison du système
par rapport à la ligne de visée, de l'épaisseur et de la composition de
l'éventuelle atmosphère de la planète.
Mesures orbitales
On retire des observations : la période orbitale, le demi-grand axe, et surtout l'inclinaison de l'orbite (voisine de 90°). Cette dernière n'est pas mesurable par la méthode des vitesses radiales.
L'atmosphère planétaire
Potentiellement, la comparaison des mesures spectroscopiques de l'étoile avant et pendant le transit peut donner accès à la composition de l'atmosphère planétaire.
Le transit de l'étoile HD 209458 a conduit à la détection d'une atmosphère planétaire étendue, qui explique l'allure de la courbe d'occultation dans la raie Lyman alpha de l'hydrogène.
Transit d'une planète devant son étoile

Crédit :
ASM
Méthode de détection d'éléments chimiques dans une atmosphère
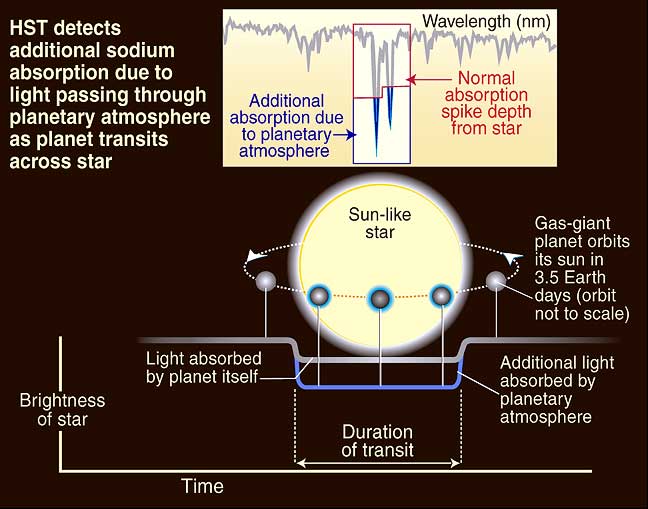
Crédit :
HST
Baisse de flux
Le passage récurrent d'une planète devant son étoile parente provoque une diminution périodique du flux reçu de l'étoile si le système est observé sous un angle adéquat, i.e. si la planète traverse la ligne de visée de l'observateur.
La diminution relative du flux émis par l'étoile dans la direction de l'observateur lors du transit de la planète est :
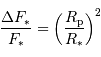
où 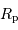 est le rayon de la planète et
est le rayon de la planète et 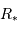 celui de l'étoile. On suppose ici que le flux était uniforme à la surface de l'étoile (le détail du calcul est traité en exercice).
celui de l'étoile. On suppose ici que le flux était uniforme à la surface de l'étoile (le détail du calcul est traité en exercice).
Ordres de grandeurs
Les systèmes les plus facilement détectables, avec une planète de type Jupiter chaud, ont un rayon de l'ordre de 10 à 20% du rayon stellaire d'une étoile froide de la séquence principale. Ils induisent des baisses de flux de l'ordre de quelques pourcents.
La variation relative de flux pour un système de type Soleil-Jupiter est de 1%, et de 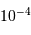 pour un système tel que Soleil-Terre.
pour un système tel que Soleil-Terre.
Sondage atmosphérique
Une information essentielle pourra également être apportée par cette méthode : la présence ou non d'une atmosphère autour de la planète, reliée à la pente de l'extinction du flux, progressive en présence d'une atmosphère. Cette détection est extrêmement importante, car on peut connaître la composition de cette atmosphère en comparant les mesures spectroscopiques de l'étoile avant et pendant le transit.
Il est en principe possible de rechercher des signes d'activités exobiologiques en détectant des composants gazeux dont l'abondance est un indice de la présence d'organismes vivants... mais hors de portée des moyens actuels.
Occultations
Animation reliant la courbe de lumière à l'évolution temporelle de la géométrie du système. L'inclinaison du plan orbital planétaire est un paramètre crucial.
La signature photométrique diffère selon que l'inclinaison est
très proche ou
voisine de 90 degrés, ou
trop éloignée.

Transit planétaire, avec une inclinaison proche de 90 degrés. La signature photométrique reste ténue. Le rapport des luminosités stellaire et planétaire est tel que l'occultation de la planète par l'étoile reste n'est pas observable.
Crédit :
ASM

Transit planétaire. L'inclinaison, voisine de 90 deg, ne conduit qu'à une occultation partielle, et donc une très faible signature photométrique.
Crédit :
ASM

Pas de transit planétaire, l'inclinaison différant trop de 90 deg. Aucune occultation, et donc aucune signature photométrique.
Crédit :
ASM
 Transit de HD 209458
Transit de HD 209458
Difficulté : ☆
Temps : 20 min
HD 209458 est une des nombreuses étoiles hébergeant une exoplanète. On cherche à caractériser le transit de cette dernière. Les notations sont les mêmes que celles des pages précédentes.
Question 1)
Retrouver l'expression de la diminution relative de luminosité 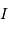 :
:
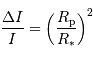
On suppose le flux (équivalent à une luminosité, ou puissance, surfacique) stellaire 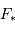 uniforme :
uniforme :
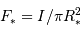 .
.
Estimer la différence de luminosité avec et sans éclipse, fonction de la
surface stellaire visible, variable, et du flux surfacique, fixe.
Question 3)
Calculer la masse volumique 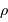 de l'exoplanète, sachant que sa masse
de l'exoplanète, sachant que sa masse 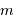 vaut
vaut 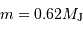 . Quelle remarque vous inspire ce résultat ?
. Quelle remarque vous inspire ce résultat ?





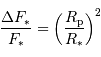
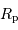 est le rayon de la planète et
est le rayon de la planète et 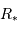 celui de l'étoile. On suppose ici que le flux était uniforme à la surface de l'étoile (le détail du calcul est traité en
celui de l'étoile. On suppose ici que le flux était uniforme à la surface de l'étoile (le détail du calcul est traité en 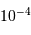 pour un système tel que Soleil-Terre.
pour un système tel que Soleil-Terre.
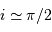 . La masse
. La masse 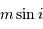 est donc dans ce cas égale à la masse réelle
est donc dans ce cas égale à la masse réelle 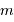 . Le transit permet également de déterminer le rayon de la planète, le rayon de l'étoile étant estimé par une autre méthode.
. Le transit permet également de déterminer le rayon de la planète, le rayon de l'étoile étant estimé par une autre méthode.


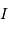 :
:
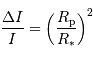
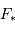 uniforme :
uniforme :
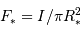 .
.
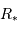
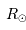
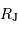
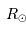

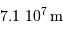
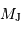
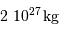
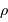 de l'exoplanète, sachant que sa masse
de l'exoplanète, sachant que sa masse 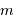 vaut
vaut 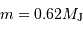 . Quelle remarque vous inspire ce résultat ?
. Quelle remarque vous inspire ce résultat ?
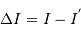 avec
avec 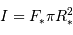 , et
, et 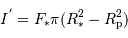 . Donc :
. Donc :
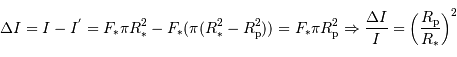
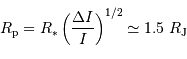
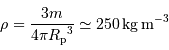
 ). C'est une géante gazeuse. Et si l'on trouvait un océan suffisamment grand, la planète y flotterait ...
). C'est une géante gazeuse. Et si l'on trouvait un océan suffisamment grand, la planète y flotterait ...