
Le modèle du corps noir |
Le FDC est un rayonnement issu d'un univers dense et chaud lequel peut être modélisé par un corps noir. Afin de comprendre les propriétés de ce reliquat des premiers temps, il faut connaître les propriétés des corps noirs et de leur rayonnement.
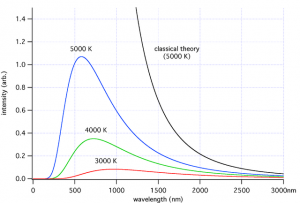
La branche de la physique qui étudie les propriétés liées à la température des corps et aux échanges d’énergie entre eux (échanges de chaleur, émissions de rayonnement) s’appelle la thermodynamique. Un corps noir y est défini comme un corps en équilibre thermodynamique qui absorbe tout le rayonnement électromagnétique qu’il reçoit, contrairement à un miroir par exemple. Noir ne signifie pas qu'il est invisible comme un trou noir mais qu'il absorbe toute la lumière. En raison de sa température, un corps noir émet un rayonnement dit thermique qui est caractérisé par sa température. Le nombre de photons produits en fonction de leur longueur d'onde est une fonction qui a une forme de cloche asymétrique. Le pic de ce rayonnement est directement lié à sa température par la loi de Wien :
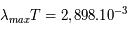 m.K
m.K
Ainsi le corps humain, qui est à une température d’environ 37°C (soit environ 37+273 = 310 K) émet un rayonnement principalement dans l’infrarouge à 9,3 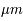 (d’où les jumelles à infrarouge utilisées pour repérer des êtres humains la nuit). La température étant inversement proportionnelle à la longueur d'onde du pic d'émission, plus un corps est chaud, plus son rayonnement a lieu vers les hautes énergies, c’est à dire vers les petites longueurs d’onde. Ainsi au fur et à mesure que l’on chauffe un morceau de fer il apparaîtra d’abord rouge, puis orange, et enfin bleu, diminuant sans cesse de longueur d'onde. Passée une certaine température, le pic se trouvera dans l'ultra-violet et l'oeil ne verra que la queue de distribution des photons des grandes longueurs d'onde.
(d’où les jumelles à infrarouge utilisées pour repérer des êtres humains la nuit). La température étant inversement proportionnelle à la longueur d'onde du pic d'émission, plus un corps est chaud, plus son rayonnement a lieu vers les hautes énergies, c’est à dire vers les petites longueurs d’onde. Ainsi au fur et à mesure que l’on chauffe un morceau de fer il apparaîtra d’abord rouge, puis orange, et enfin bleu, diminuant sans cesse de longueur d'onde. Passée une certaine température, le pic se trouvera dans l'ultra-violet et l'oeil ne verra que la queue de distribution des photons des grandes longueurs d'onde.
Les poussières dans le milieu interstellaire sont un exemple de corps noir dont la température est de quelques centaines de Kelvin. Elles émettent principalement à des longueurs d'onde dans l'InfraRouge. Les étoiles dont la température superficielle peut prendre des valeurs entre quelques milliers et quelques dizaines de milliers de Kelvin sont aussi des corps noirs (voir figure). Leurs pics d'émission se situent entre 1000 et 100 nm. A noter que l'atmosphère des étoiles crée des raies d'émission et d'absorption dans le spectre d'une étoile, ce qui l'éloigne du corps noir parfait. Cependant, elles restent de meilleurs corps noir que le corps humain ou le fer.
La loi de rayonnement du corps noir, découverte par Max Planck à la toute fin du XIXe siècle, relie l'énergie rayonnée par unité de volume, 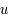 , ou le nombre de photon par unité de volume à la fréquence,
, ou le nombre de photon par unité de volume à la fréquence, 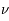 , des photons pour un corps noir d'une température
, des photons pour un corps noir d'une température 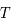 . Elle englobe la relation de Rayleigh-Jeans qui décrivait cette loi pour les grandes longueurs d'onde, au-delà du pic central de rayonnement. Elle est historiquement importante car la compréhension physique de la partie des courtes longueurs d'onde a requis l'ajout d'un concept nouveau en physique, le quantum d'énergie qui sera développé ultérieurement pour la mécanique quantique. Le loi de Planck est la suivante :
. Elle englobe la relation de Rayleigh-Jeans qui décrivait cette loi pour les grandes longueurs d'onde, au-delà du pic central de rayonnement. Elle est historiquement importante car la compréhension physique de la partie des courtes longueurs d'onde a requis l'ajout d'un concept nouveau en physique, le quantum d'énergie qui sera développé ultérieurement pour la mécanique quantique. Le loi de Planck est la suivante :
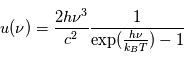
où 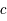 est la vitesse de la lumière (300 000 km/s),
est la vitesse de la lumière (300 000 km/s), 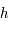 la constante de Planck (
la constante de Planck (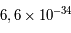 J.s) et
J.s) et 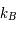 la constante de Boltzmann (
la constante de Boltzmann (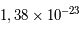 J/K).
J/K).