L'information recherchée dans un signal s'exprime de diverses façons.
Cette section présente les grands principes en oeuvre
et les techniques instrumentales associées, pour traiter au mieux les photons selon :
- Leur direction d'origine
- Leur quantité.
- Leur couleur.
- Et toute combinaison de ces 3 propriétés, sans oublier éventuellement leurs variations temporelles.
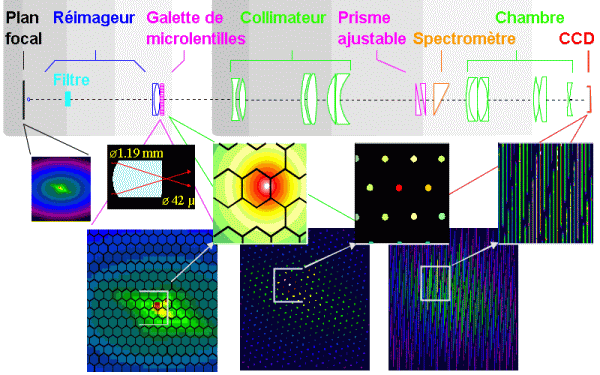
Principe de la spectrométrie intégrale de champ.
Crédit :
CFHT
L'information portée par les photons peut être traitée de diverses façons, ainsi que le montrent les illustrations suivantes.
L'amas des Hyades
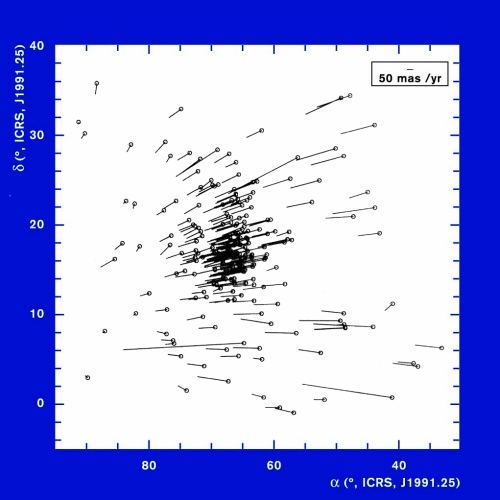
Le mouvement propre des étoiles de l'amas des Hyades a pu être reconstruit par le satellite Hipparcos.
Crédit :
ESA
Cartographie grand champ

Le ciel profond vu par le télescope spatial. Remarquer la corrélation entre la couleur et la luminosité des objets.
Crédit :
HST
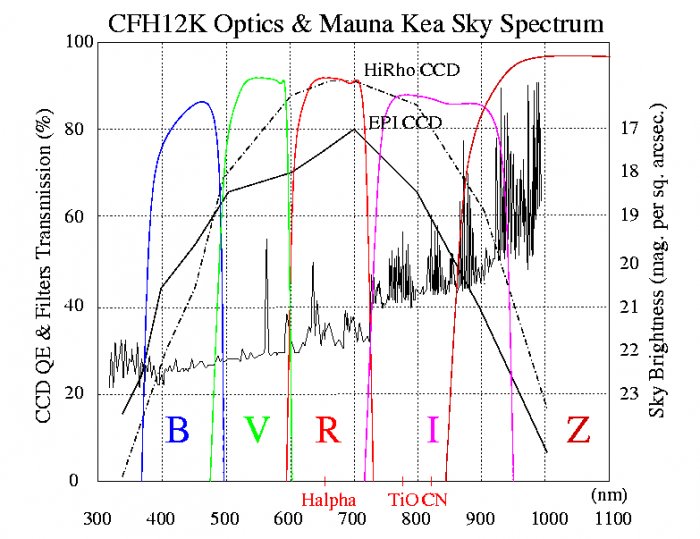
Système de filtres BVRI normalisés permettant de mesurer précisément les
magnitudesassociées.
Crédit :
CFHT

Assemblage de filtres pour des mesures dans le système BVRI
Crédit :
ESO/Cyril Cavadore
- Astrométrie : Mesure de position et mouvement. Le satellite Hipparcos a relevé la position, à la milliseconde d'arc près, de 120 000 étoiles (jusqu'à la magnitude 12).
- Imagerie : Cartographie, pour une étude morphologique, statistique, sans ou à très faible résolution spectrale, ou bien dans des filtres très précis.
- Photométrie : Mesure de flux lumineux dans un système de bandes spectrales
- Spectrométrie : Identification des photons selon leur couleur.
Ex. : observation du spectre IR de Procyon.
- Spectroimagerie : Les photons sont traités pour recueillir simultanément les informations spatiale et spectrale qu'ils véhiculent.
Spectro 2-D
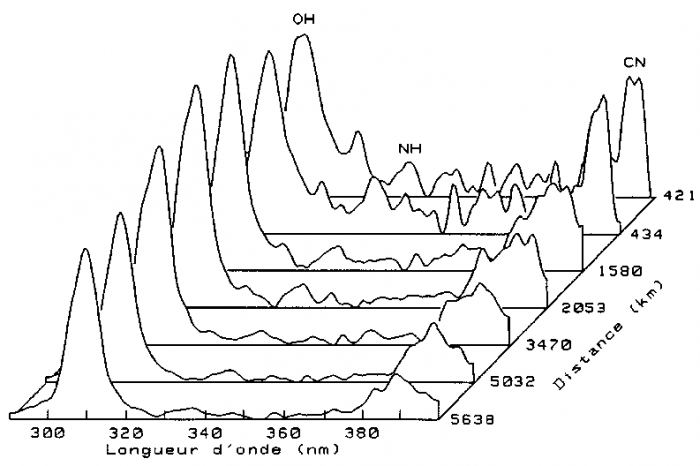
Chaque point de la fente source est dispersée, dans une direction perpendiculaire à celle de la fente. Une dimension du CCD traduit la variable spatiale, l'autre la variable spectrale.
Crédit :
ESO
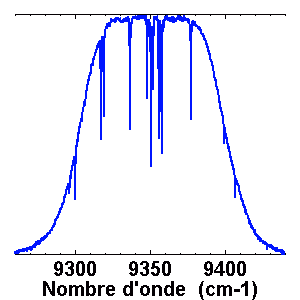
Procyon, aux alentours de
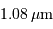
. Ce domaine spectral est sélectionné par un filtre étroit. Noter l'unité spectrale, inverse de la longueur d'onde.
Crédit :
CFHT/ASM
 Objectifs
Objectifs
Distinguer différents principes instrumentaux.
Différents principes
- Astrométrie : Repérages de positions, pour la mesure de distance et de mouvement. La mesure des parallaxes des étoiles du proche voisinage solaire est une étape indispensable pour la détermination des distances interstellaires, et le point de départ obligé d'un juste arpentage de l'Univers.
- Imagerie :
L'imagerie, ce n'est pas que de belles images d'intérêt cosmico-esthétique, mais le support de diverses activités : relevés statistiques, morphologie, activité... Aujourd'hui se développe l'imagerie grand champ, à base de
mosaïques de CCD.
- Photométrie : Mesure de flux lumineux, dans des bandes spectrales bien définies (p.ex. le système BVRI utilisé dans le visible et le proche infrarouge).
Les mesures photométriques nécessitent d'excellentes conditions atmosphériques. Les différents éléments de la chaîne d'acquisition (transparence atmosphérique, efficacité de l'instrumentation et du détecteur) interdisent toute mesure absolue directe. Un étalonnage sur une source connue est nécessaire : source céleste bien référencée, ou source d'étalonnage interne à l'instrument.
- Bolométrie : Mesure de flux lumineux,
l'énergie des photons incidents (essentiellement les domaines X et IR)
étant convertie en agitation thermique dans le détecteur, dont la résistance électrique varie avec la température. Les bolomètres n'ont intrinsèquement aucune sélectivité spectrale.
- Spectrométrie :
Différents types de spectromètres sont utilisés
en astronomie : spectromètre à résonance,
spectromètre interférentiel
(spectromètre par transformée
de Fourier, Fabry-Pérot, spectromètre à réseau), spectromètre hétérodyne.
Selon différents
critères (largeur spectrale admissible, résolution spectrale) l'une ou l'autre des
techniques s'impose.
- Spectroimagerie : La spectroimagerie permet l'obtention de l'information spectrale pour toute une région spatiale. Selon les techniques (spectrométrie
multi-objets, spectro intégrale de champ), cette région est un ensemble
de différentes cibles ponctuelles, un objet étendu...
Quels principes, pour quelle mesure ?
La liste qui précède est austère. Les pages qui suivent illustrent comment ces techniques sont mises en pratique, et dans quel but.

Le champ stellaire analysé, autour de l'étoile HD 49933 (abondamment observée par une mission spatiale du CNES).
Crédit :
CDS
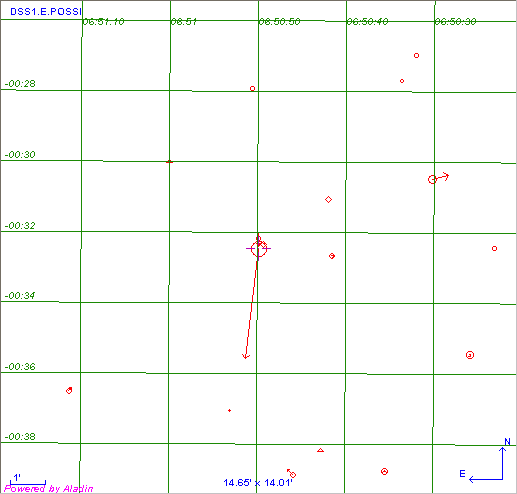
La carte des étoiles précédemment répertoriées, avec de plus leur mouvement propre.
Crédit :
CDS
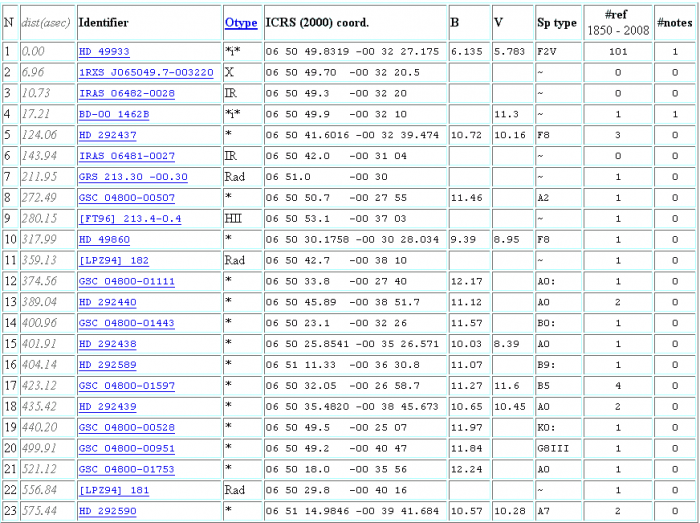
Le catalogue des étoiles précédemment répertoriées.
Crédit :
CDS
Un exemple : environnement d'une étoile
Les données astrométriques permettent une foultitude de choses, comme par exemple de précisément caractériser un champ autour d'un objet. Les figures ci-jointes décrivent de diverses manières l' environnement d'une étoile,
une carte, ou par
les coordonnées.
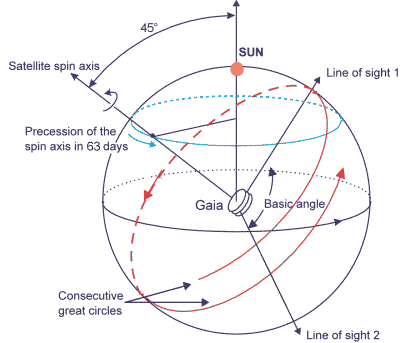
Le satellite Gaia, au point de
Lagrange L2, est animé d'un mouvement de rotation régulier, avec un axe (spin axis) orienté à 45 deg par rapport à la direction du Soleil. Il observe simultanément 2 régions du ciel (line of sight 1 et 2). Le mouvement de rotation induit le balayage de 2 grands cercles. La précession du mouvement de rotation induit l'évolution de ces grands cercles, pour observer tout le ciel.
Crédit :
ESA

Le montage de Gaia repose sur une structure octogonale très stable, pour la définition de l'angle entre les 2 lignes de visée astrométriques. Une 3ème ligne de visée est utilisée pour des mesures spectrométriques. La collecte du signal sur chaque ligne de visée implique 3 miroirs : les miroirs primaire et tertiaire se situent dans un même plan, et font face au miroir secondaire et au détecteur. Vu le nombre gigantesque de cibles à mesurer, le plan focal est composé d'une mosaïque de plusieurs dizaines de CCD. Le mode de lecture des CCD est original : les lignes du CCD sont positionnées exactement parallèlement au déplacement apparent de l'image suite à la rotation propre du satellite, et la pose et le transfert des charges d'un pixel à l'autre suivent le déplacement de l'image stellaire le long de la ligne du CCD.
Crédit :
EADS/Astrium
Le projet Gaia
Le principe de mesure de Gaia repose sur le balayage du ciel simultanément le long de deux lignes de visée. Le scénario de pointage met en oeuvre la rotation propre et la précession du satellite. Le montage optique s'appuie sur une structure stable.
 Définition
Définition
L'astrométrie a pour but de mesurer la position des astres, leur parallaxe et donc leur distance, leur mouvement propre. Elle opère un travail indispensable de repérage et d'arpentage.
Comment ?
L'agence spatiale européenne a exploité le satellite Hipparcos durant les années 1990, et lancé la mission Gaia fin 2013. Ces 2 missions ont pour but principal l'arpentage de l'Univers, obtenu par une très grande précision astrométrique.
Hipparcos comme Gaia sont des missions spatiales. L'écran de l'atmosphère terrestre est évité, la déviation d'un rayon lumineux au travers des couches atmosphériques étant bien trop importante par rapport à la précision recherchée, de l'ordre de la milliseconde d'arc.
La précision des missions Hipparcos et Gaia s'appuie sur le principe de l'observation simultanée de 2 champs stellaires, dans 2 directions faisant entre elles un angle fixé et stable (106.5 deg).
Comme un compas sert à repérer des distances (linéaires ou angulaires), de proche en proche les positions relatives des objets sont fixées les unes par rapport aux autres.
Gaia doit mesurer la précision d'un milliard d'objets dans la galaxies (soit 1% de son contenu stellaire), avec une précision de quelques millionièmes secondes d'arc pour les cibles les plus brillantes.
Performances attendues avec Gaia, pour une étoile de type G2
| magnitude | 10 | 15 | 20 |
| parallaxe (mas) | 0.007 | 0.027 | 0.3 |
Positions et mouvements
La
simulation ci-dessous permet de lire les positions et mouvements repérés par le satellite européen Hipparcos dans l'amas ouvert des Hyades. Noter que la précision des positions effectivement repérées par Hipparcos est infiniment meilleure que celle restituée par l'appliquette.

 Précision astrométrique et inégalité de Heisenberg
Précision astrométrique et inégalité de Heisenberg
Difficulté : ☆☆☆
Temps : 45 min
Cet exercice se propose de montrer que la précision astrométrique
d'un satellite tel Hipparcos ou Gaia peut être estimée par
l'application des inégalités de Heisenberg. On s'intéresse pour
ceci à la propagation d'un photon, issu d'un objet ponctuel à
l'infini, dont la trajectoire intercepte le miroir primaire de
détection (!). On munit l'espace d'un repère orthonormé 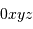 telle que le plan
telle que le plan 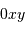 corresponde au miroir primaire de la
détection. La quantité de mouvement du photon incident est
quasiment parallèle à
corresponde au miroir primaire de la
détection. La quantité de mouvement du photon incident est
quasiment parallèle à 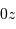 . On suppose que la formation d'image
suit parfaitement les lois de l'optique géométrique.
. On suppose que la formation d'image
suit parfaitement les lois de l'optique géométrique.
Question 1)
On s'intéresse à l'interception du photon selon la direction 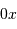 .
Peut-on connaître la position de l'impact et de la réflexion du
photon sur le miroir? En déduire que le front d'onde incident est
découpé en tranche de largeur la dimension du miroir, que la
position selon l'axe
.
Peut-on connaître la position de l'impact et de la réflexion du
photon sur le miroir? En déduire que le front d'onde incident est
découpé en tranche de largeur la dimension du miroir, que la
position selon l'axe 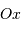 est inconnue, et que donc elle est
affublée d'une incertitude de position
est inconnue, et que donc elle est
affublée d'une incertitude de position 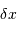 .
.
[2 points]
Réfléchir (!) à la formation d'image. Considérer une lentille
équivalente pour se simplifier la vie.
Question 2)
On rappelle qu'un échantillonnage par valeur entière correspond à
un bruit de numérisation de 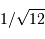 . En déduire
l'incertitude de mesure de la composant selon
. En déduire
l'incertitude de mesure de la composant selon 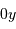 de la quantité
de mouvement du photon.
de la quantité
de mouvement du photon.
[1 points]
L'échantillonnage en position se fait ici par pas de largeur 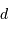 .
.
Question 3)
Par inégalité de Heisenberg, les incertitudes de position et
quantité de mouvement doivent vérifier :
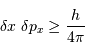
avec la quantité de mouvement totale 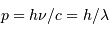 .
En déduire que l'incertitude de repérage de l'angle d'incidence du
photon vaut :
.
En déduire que l'incertitude de repérage de l'angle d'incidence du
photon vaut :
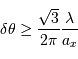
[3 points]
Déterminer d'abord 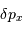 .
.
Déterminer 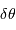 en fonction de
en fonction de 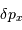 .
.
Question 4)
Faire l'application numérique pour Gaia, observant à la longueur
d'onde moyenne de 600 nm, avec 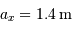 . Cela est-il
compatible avec les performances annoncées, de l'ordre de
. Cela est-il
compatible avec les performances annoncées, de l'ordre de 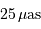 à la magnitude
à la magnitude 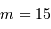 ? Pourquoi ?
? Pourquoi ?
[1 points]
Question 5)
La question précédente dimensionne l'incertitude pour 1 photon. On
montre plus loin dans le cours que pour 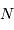 photons effectivement
détectés, l'incertitude est divisée par
photons effectivement
détectés, l'incertitude est divisée par 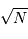 . Combien de
photons doivent être détectés pour aboutir à la performance
annoncée.
. Combien de
photons doivent être détectés pour aboutir à la performance
annoncée.
[1 points]
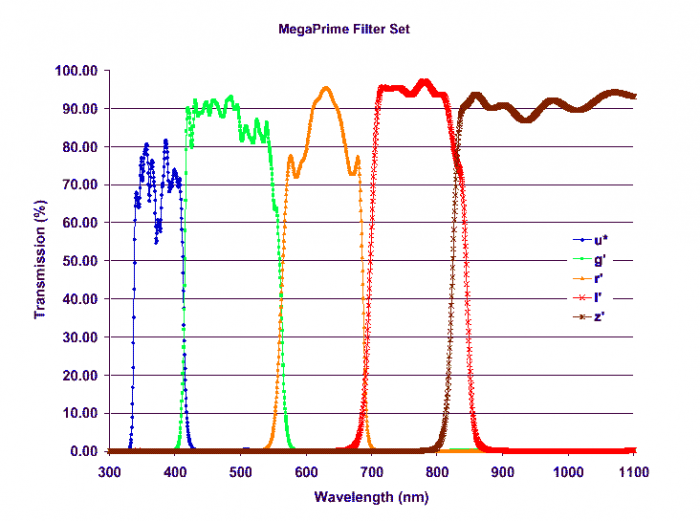
Le système de filtres de la caméra MEGACAM du télescope CFH
Crédit :
CFHT
Mesure de flux dans un système de filtres
Toute mesure photométrique doit s'appuyer sur un système de filtres précis, calibrés par rapport aux filtres des autres systèmes utilisés. Le projet MEGACAM au
télescope CFH
utilise le système ci-joint, couvrant du très proche UV au proche IR.
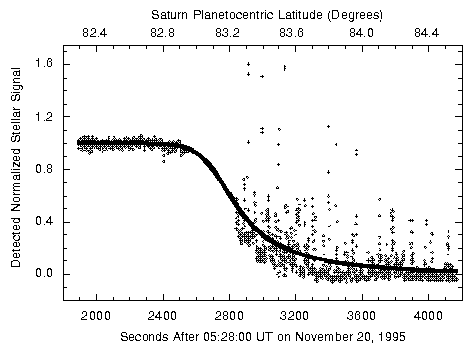
Courbe d'occultation : éclipse de l'étoile GSC5249-01240 par Saturne.
Crédit :
NASA/IRTF
Mesure de variations de flux
Les occultations, qui réunissent sur un même axe un objet du système solaire et une étoile, comme une éclipse réunit la Lune et le Soleil, ne sont pas que de simples événements fortuits : leur observation est riche en enseignement (métrologie, sondage atmosphérique...).
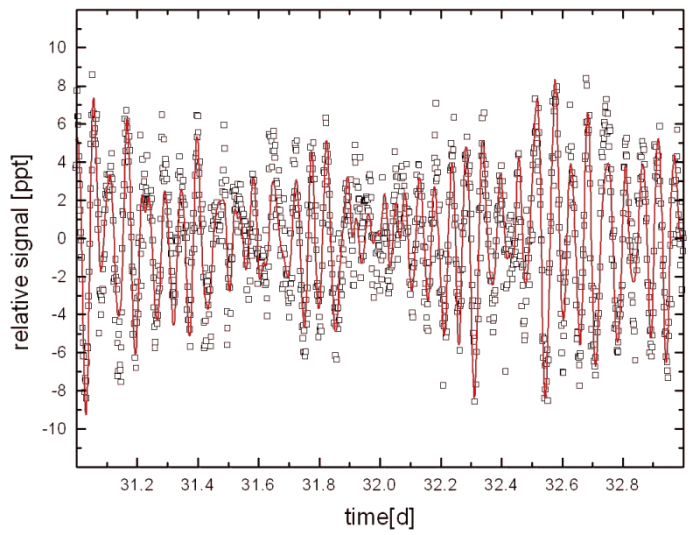
Échantillon de la série temporelle de la variabilité d'une étoile observée par le micro-satellite canadien MOST. L'échelle des ordonnées représente les variations relatives comptée en pourmille. La courbe rouge donne une estimation des variations observées : elle s'interprète comme les battements entre différents modes de pulsation stellaire.
Crédit :
MOST
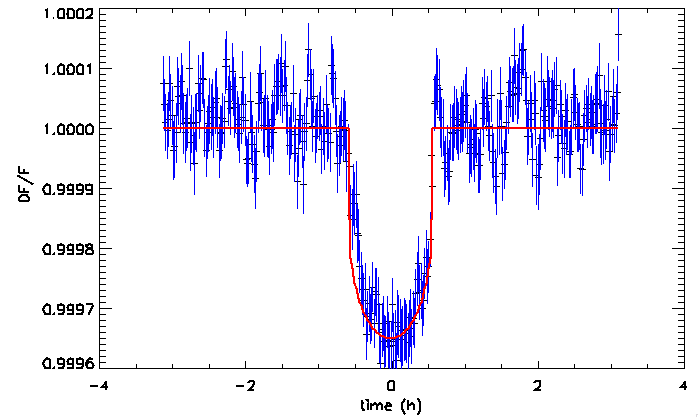
Transit de la planète CoRoT-exo-7b, détectée par le satellite CoRoT.
Crédit :
CoRoT/CNES
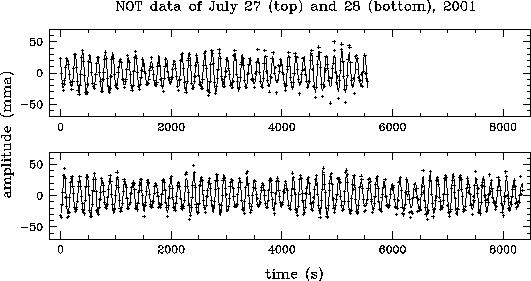
Courbe de variabilité d'une naine blanche. Les oscillation stellaires modulent le signal. Le rapport signal à bruit est suffisant pour mettre en évidence directement les oscillations. Plusieurs (9 en fait) observatoires ont été mis à contribution pour éviter au mieux - aléa météorologique mis à part - les interruptions diurnes sur les 25 jours & nuits d'observation.
Crédit :
WET
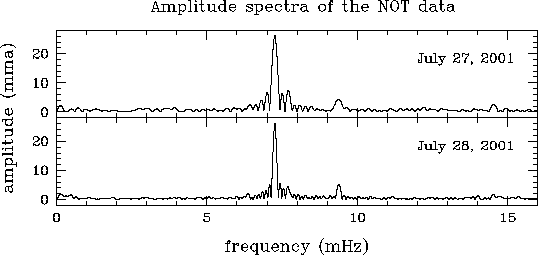
Crédit :
WET
Microvariabilité
Les mesures photométriques recherchent souvent des variabilités, dont l'étude ouvre de multiples champs d'investigation. Plusieurs satellites passent actuellement leur temps à mesurer des flux stellaires avec une précision de plus en plus grande. Le satellite CoRoT a ainsi découvert une très petite planète.
La microvariabilité d'une naine blanche (PG1159) est étudiée pour l'analyse de ses oscillations : la série temporelle enregistrée sur 8 nuits aboutit au spectre de Fourier.
 Définition
Définition
Photométrie : étude de la magnitude d'un astre dans un système de bandes spectrales.
Pourquoi la photométrie ?
Connaître précisément le nombre de photons de couleur donnée qui arrivent en un intervalle de temps donné permet de remonter à des considérations énergétiques.
Le problème est très souvent complexe, car il nécessite de tenir compte précisément de la transparence atmosphérique, de la fonction de transfert du collecteur et de l'instrument, de la réponse spectrale du détecteur...
Comment ?
Les effets mentionnés ci-dessus illustrent la complexité, voire l'impossibilité, d'une mesure photométrique absolue. Les mesures effectuées sont des mesures relatives, où la luminosité de l'objet, intégrée ou spectrale, est comparée à une référence.
Cette référence peut être une cible stellaire (telle l'étoile Véga p.ex, qui définit la magnitude apparente visuelle 0). Les mesures bolométriques, dans l'IR ou le submillimétrique, comparent le flux étudié à celui d'un corps noir calibré.
Variation photométrique
L'étude de la variabilité et de la
microvariabilité
est très fructueuse, pour observer des phénomènes à haute
fréquence, associés à des variations intrinsèquement rapides ou
bien dues à des phénomènes transitoires.

Techniques
Mesurer un flux nécessite de la méthode, et cette dernière dépend du signal étudié. On peut pratiquer :
- La photométrie d'ouverture consiste à considérer tout le flux dans une ouverture donnée. La part de bruit dans cette ouverture sera incluse, peut être indûment, dans l'énergie du signal.
- La photométrie à seuil consiste à considérer comme signal tout ce qui dépasse un niveau de référence. Le choix du seuil est crucial : trop bas, il va considérer comme composante du signal ce qui n'est que du bruit ; trop haut, il ampute le signal.
- La photométrie par ajustement modélise la fonction d'étalement du point attendue, pour aller au plus juste de la mesure. Elle est plus précise que les autres méthodes, mais pas nécessairement simple à mettre en oeuvre. Elle peut être impossible à réaliser à bord d'un satellite, en l'absence de la puissance de calcul nécessaire.

Nuage moléculaire sculpté par le rayonnement ultraviolet ionisant de jeune étoiles en formation. Les doigts de matière qui résistent à l'érosion UV sont dans l'ombre portée par des régions plus denses. Ces dernières sont les plus violemment illuminées, et apparaissent les plus brillantes.
Crédit :
HST
Résolution spatiale, structures et détails
Imager permet de tracer la distribution de matière qui rayonne, qui absorbe... Une image en fausse couleur résulte de la superposition de 3 images prises dans 3 filtres différents.

Autrefois, avant l'introduction de la photographie à usage astronomique, à la fin du XIXe siècle, imager signifiait dessiner !
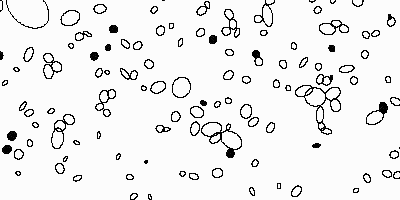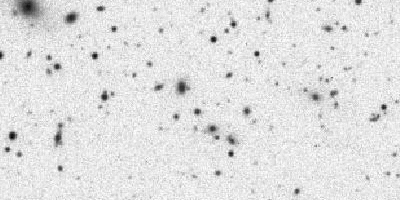
Champ stellaire, et identification des étoiles (points noirs) et des galaxies, via un logiciel de reconnaissance automatique de forme.
Crédit :
IAP
Identification
L'imagerie permet d'identifier les objets, pour les classer, pour faire le lien entre diverses observations à diverses longueurs d'onde... Un problème courant est de distinguer les sources stellaires des sources galactiques.

Déplacement d'un objet de Kuiper au cours d'une nuit. C'est justement son mouvement propre qui permet d'identifier un tel objet, de magnitude typique supérieure à 20.
Crédit :
CFHT

Rotation propre de l'astéroïde Eros, observée par la sonde NEAR.
Crédit :
NEAR/Nasa
Mouvements
L'imagerie, répétée sur un même champ, permet la découverte des petits corps du système solaire, en mouvement apparent sur fond d'étoiles fixes. C'est p.ex. ainsi qu'ont été découverts les objets de Kuiper, éléments du système solaire situés au-delà des planètes géantes, en deçà des comètes, et s'en distinguant par des orbites relativement proche de l'écliptique et d'excentricité modérée.

Rotation de Jupiter. Suivi des impacts des fragments de la comète SL9 sur Jupiter, en juillet 1994.
Crédit :
ESO
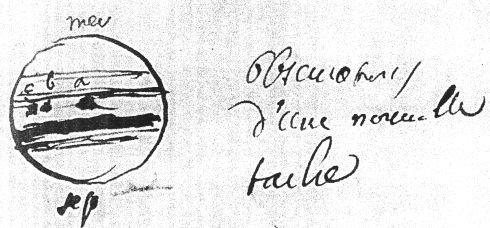
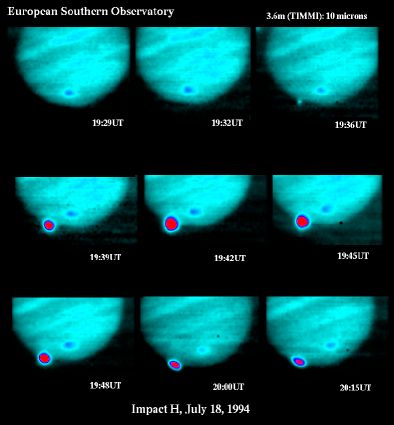
Observation d'une nouvelle tache sur Jupiter, par Cassini, en mars 1684. Et chute, observée en direct, d'un fragment cométaire sur Jupiter 3 siècles plus tard (juillet 1994, observation dans l'IR thermique à l'ESO) ; un fragment précédent a provoqué la tache à la même latitude que l'impact.
Crédit :
Bibliothèque de l'Observatoire de Paris / ESO
Événements
L'imagerie permet aussi de repérer des événements particuliers, comme p.ex. l'apparition de taches sur Jupiter.
 Objectifs
Objectifs
Tentative, désespérée, de classification des divers et nombreux champs d'application de l'imagerie en astrophysique
 Définition 😁
Définition 😁
Imagerie : fournir des images dans des systèmes de filtres standards, ou au-moins précisément référencés.
Pourquoi l'imagerie ?
L'imagerie fournit des images. Pour obtenir une image, il faut au préalable avoir reçu 10 bons points. On peut échanger 10 images contre un petit livre.
Les images en astrophysique apportent l'information spatiale, qui permet le traçage et l'identification de la matière lumineuse. Cette information dépend essentiellement de la longueur d'onde d'observation.
La résolution spatiale, couplée avec une faible résolution spectrale, donne par exemple accès à des informations de température ; avec une forte résolution spectrale : traçage fin d'un élément, mesures Doppler...
Comment ?
Obtenir une image est relativement trivial dans certains cas, pas du tout dans d'autres.
Ceci peut être dû à la mise en forme du signal.
Dans les domaines X et surtout 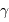 , la capacité d'imagerie des détecteurs est très limitée, et il est souvent difficile de bien localiser une source même intense. Du côté des très grandes longueurs d'onde, la tache d'Airy due à la diffraction peut atteindre une extension angulaire très grande ce qui limite la résolution spatiale.
, la capacité d'imagerie des détecteurs est très limitée, et il est souvent difficile de bien localiser une source même intense. Du côté des très grandes longueurs d'onde, la tache d'Airy due à la diffraction peut atteindre une extension angulaire très grande ce qui limite la résolution spatiale.
La capacité d'imagerie dépend aussi de la technologie des détecteurs. Si en lumière visible les mosaïques CCD atteignent 2k x 4k, les performances sont bien plus limitées dans les longueurs d'onde infrarouges. En submillimétrique et radio, les détecteurs étant monopixels, les images sont construites par juxtaposition d'images élémentaires.
Systèmes de filtres
L'imagerie est le plus souvent menée dans des systèmes de filtres si possible référencées, afin de pouvoir mener des comparaisons entre diverses observations. Ces filtres couvrent continûment le spectre, en bande large.
Spectrohéliogrammes

Le disque solaire, dans diverses bandes spectrales : raie Halpha à 656.3 nm ; et raie K du calcium à 393.4 nm (K3 dans le minimum de la raie ; K1v dans l'aile de la raie côté violet). La morphologie des structures dépend intimement de la longueur d'onde d'observation.
Crédit :
Observatoire de Paris

Le disque jovien est quasiment éteint à la longueur d'onde
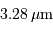
, alors que Io apparaît bien plus brillant à cette longueur d'onde.
Crédit :
ESO

Titan observé en optique adaptative dans différentes domaines de longueur d'onde du proche infrarouge. Lorsque le domaine spectral est sensible à un élément dans la stratosphère, le
limbe apparaît plus brillant.
Crédit :
ESO
Objets brillants
L'imagerie multispectrale, gourmande en photons, est menée sur des objets brillants, comme typiquement les objets du système solaire.
Selon la longueur d'onde d'observation, les disques solaire, jovien ou de Titan présentent différents aspects. Les domaines spectraux sont ici adaptés au phénomène étudié.

L'intérêt de l'imagerie multi-spectrale est de permettre une modélisation précise de l'objet observé. Par application de code de transfert de rayonnement, cette modélisation permet typiquement de contraindre la température et la composition de l'objet. Le diaporama ci-contre illustre une application sur la calotte martienne sud, observée par l'instrument OMEGA à bord de la sonde Mars Express.
La Voie Lactée

Images reconstruites de la Voie Lactée en différentes bandes spectrales.
Crédit :
NASA
La Voie Lactée
Selon la longueur d'onde d'observation, la Voie Lactée se présente sous différents aspects : chaque longueur d'onde apporte des informations complémentaires sur sa structure.
- Continu radio à 408 MHz : l'émission provient spécialement de la diffusion des électrons libres (émis lors des supernovae) dans le plasma interstellaire chaud, ou alors d'électrons accélérés dans des régions avec un fort champ magnétique. La boucle dans l'hémisphère galactique nord signale le plasma chaud résiduel d'une supernova ayant explosé relativement proche du Soleil il y a quelques milliers d'années.
- Hydrogène atomique à 21 cm (transition hyperfine de l'hydrogène atomique) : signature de milieu interstellaire froid, cette raie signale la présence de nombreux ensembles de gaz et de poussières.
- Continu radio à 2.5 GHz : signe la présence du gaz chaud et ionisé dans les régions de formation stellaire.
- Hydrogène moléculaire : mesuré indirectement, via la transition J=1-0 du monoxyde de carbone. Cette raie donne la carte des nuages d'hydrogène froids et denses.
- Infrarouge lointain : l'émission provient principalement des nuages du milieu interstellaire réchauffés par les étoiles nouvellement formées des régions de genèse stellaire.
- Infrarouge thermique (12, 60 et 100 micromètres) : l'émission provient également des nuages du milieu interstellaire réchauffés, mais signale plus particulièrement la présence de molécules complexes.
- Proche infrarouge (1.5, 2.2 et 3.5 micromètres) : la majeure partie de l'émission provient des étoiles de type spectral K, froides et peu massives. L'absorption par la matière interstellaire est faible dans ces domaines de longueur d'onde.
- Visible (600 nm): la lumière stellaire visible est fortement absorbée par les nuages du milieu interstellaire. L'efficacité du processus d'absorption limite la portée de cette carte aux plus proches régions de l'environnement solaire.
Les régions les plus obscurcies en lumière visible correspondent aux régions les plus brillantes en infrarouge.
- X (0.25, 0.75 et 1.5 keV) : l'émission de ces rayons X de faible énergie est principalement issu des nuages chauds ; elle est absorbée par la matière interstellaire, dont la concentration est d'autant plus forte que les régions apparaissent sombres.
- Rayonnement gamma : les photons au delà de 100 MeV sont issus de la collision entre les rayons cosmiques produits par les pulsars de la Voie Lactée et la matière interstellaire.
Imagerie spectrale
L'imagerie spectrale, comme son nom l'indique, fournit des images enregistrées dans un domaine spectral bien précis, défini par un filtre adapté aux propriétés de l'objet. Cela permet de tracer la distribution de matière contribuant à une signature spectrale donnée.
Cette technique est coûteuse en photons, et l'utilisation de filtres étroits nécessite une source brillante (dans le cas du soleil, ce genre de problème ne se pose bien sûr pas).
Clair obscur
L'imagerie multispectrale combine les avantages de l'imagerie et de la spectrométrie. Comme le nombre de photons est divisé et spatialement et spectralement, la source se doit d'être lumineuse pour des observations avec un rapport signal à bruit suffisant.
 La Voie Lactée en couleurs
La Voie Lactée en couleurs
Difficulté : ☆☆
Temps : 20 min
Exercice de synthèse, basé sur les images multi-spectrales de la Voie Lactée, en 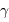 , X, visible, proche, moyen et lointain infrarouge, raie de
, X, visible, proche, moyen et lointain infrarouge, raie de 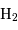 , H atomique, et radio.
, H atomique, et radio.
Question 1)
Dans quel système de coordonnées ces cartes sont-elles représentées ?
[1 points]
Question 2)
Quels domaines spectraux sont dominés par, respectivement, des sources ponctuelles intenses, une émission de type corps noir, l'absorption par des molécules ou des poussières, la réémission de ces derniers ?
[3 points]
Spectre du Soleil à haute résolution
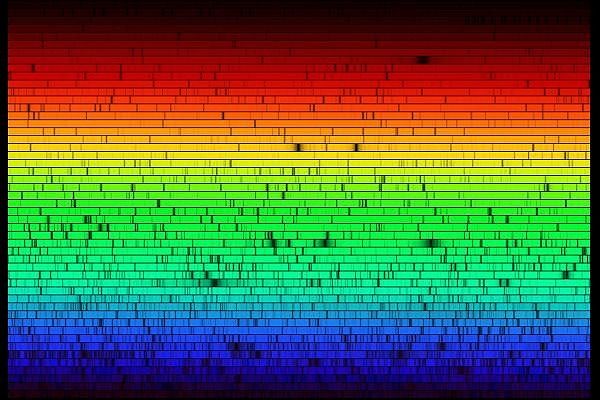
Le spectre solaire à haute résolution spectrale, observée avec un spectromètre à dispersion croisée. Les différents ordres d'interférence du spectromètre à haute dispersion ont été désenchevêtrés par la dispersion croisée.
Crédit :
NOAO
Dispersion croisée
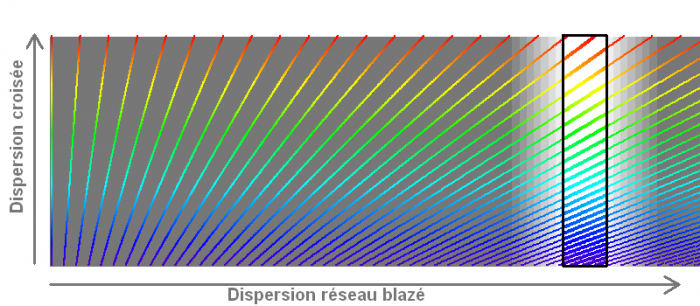
Schéma de principe :
une double dispersion permet l'enregistrement du spectre entier sur une caméra CCD. Un
réseau blazé disperse la lumière à haute résolution ; une dispersion à plus basse résolution, réalisée à l'aide d'un prisme, permet de distinguer les ordres entre eux. Le détecteur enregistre le signal dans les ordres élevés : chacun porte l'information spectrale, à haute résolution, dans un domaine de couleur différent. L'ensemble des ordres ainsi collectés permet de reconstituer le
spectre entier. Le réseau est blazé de façon à optimiser le rendement énergétique instrumental.
Crédit :
ASM
Réseau blazé
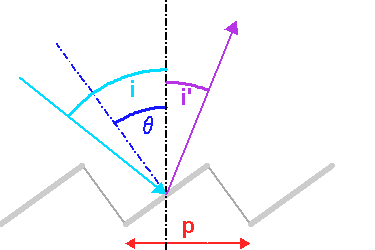
Profil d'un réseau blazé. Le profil en crête permet de réfléchir l'énergie dans un ordre d'interférence non nul.
Crédit :
ASM
Du bon usage des progrès technologiques
Les spectromètres pour la haute résolution spectrale ne datent pas d'hier. Mais l'avènement des caméras CCD, qui permettent d'enregistrer un signal sur 2 dimensions, a renouvelé le principe instrumental de la spectrométrie à haute résolution,
en ajoutant à la dispersion principale
une dispersion croisée, qui permet l'enregistrement simultané de tout le domaine spectral sur une caméra CCD.
Un spectromètre à réseau disperse la lumière dans ses ordres élevés, et les différents ordres sont séparés par une dispersion croisée obtenue à plus basse résolution. L'avantage d'une telle instrumentation est d'aboutir à un enregistrement simultané de tout le spectre, comme p.ex. ce spectre solaire.
Le spectromètre HARPS

Le spectromètre HARPS (High Accuracy Radial velocity Planet Searcher) est dédié à la recherche d'exoplanètes, par la méthode de mesure des vitesses radiales.
Crédit :
ESO/HARPS
Spectre obtenu par HARPS

Image d'un
spectre-échelle à haute résolution spectrale obtenu avec une caméra CCD. Le spectre de l'étoile apparaît ici sous l'aspect de bandes sombres.
L'étalonnage en longueur d'onde est apporté par les raies en émission d'une lampe spectrale (Thorium Argon), dont le spectre est intercalé avec celui de l'étoile, et enregistré simultanément.
Crédit :
ESO/HARPS
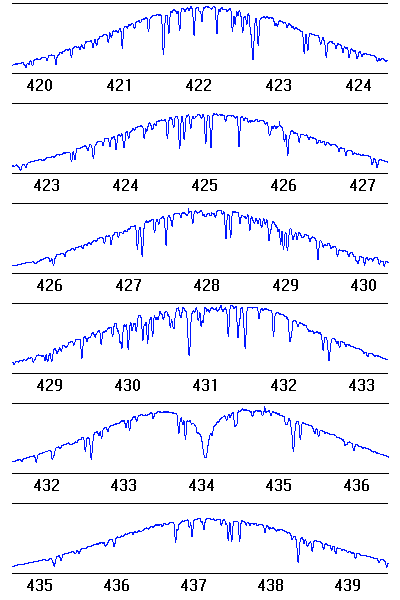
Spectre blazé obtenu avec le spectromètre Harps : la diffraction par chaque trait du réseau est responsable du profil d'étalement du flux.
Crédit :
ESO/HARPS
Le spectromètre HARPS
Le spectromètre HARPS dédié à la recherche d'exoplanètes est à l'heure actuelle le meilleur instrument de sa catégorie. Il atteint la résolution 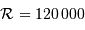 , en proposant une excellente stabilité. Les mesures sont stables et reproductibles, sur une durée de plusieurs années, à mieux que le milliardième près. Les spectres de HARPS sont obtenus avec les différents ordres d'interférences repliés sur une image ; l'image, traitée, conduit au spectre.
, en proposant une excellente stabilité. Les mesures sont stables et reproductibles, sur une durée de plusieurs années, à mieux que le milliardième près. Les spectres de HARPS sont obtenus avec les différents ordres d'interférences repliés sur une image ; l'image, traitée, conduit au spectre.
 Définition
Définition
Spectrométrie : étude des spectres.
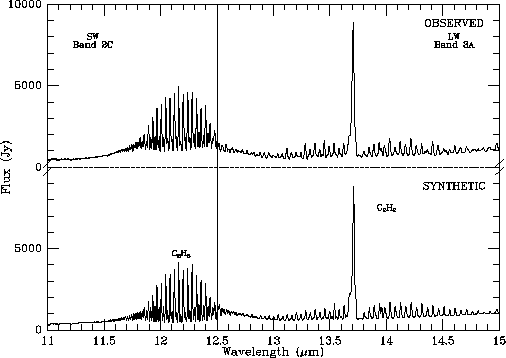
Spectre IR thermique de Saturne observé par le satellite ISO de l'Agence Spatiale Européenne, et interprétation des raies dues aux hydrocarbures présents dans la troposphère.
Crédit :
ESA
Pourquoi la spectrométrie à haute résolution ?
Bien distinguer l'identité spectrale des photons permet de remonter à la nature des éléments construisant le rayonnement, par absorption ou par émission.
La spectrométrie à haute résolution permet aussi, via l'analyse Doppler, des mesures très précises de vitesses radiales, comme p.ex. celles qui ont conduit à la découverte des planètes extrasolaires.
Le principe
Le principe du spectromètre HARPS (ESO/Observatoire de Genève) est expliqué ci-joint.
Principe du spectromètre HARPS 
 Le spectromètre HARPS
Le spectromètre HARPS
Difficulté : ☆☆☆
Temps : 45 min
Le spectromètre HARPS, mis en service au printemps 2003 à La Silla, l'un des sites chiliens de l'ESO, a pour but la recherche des exoplanètes. On se propose ici de retrouver quelques-unes des qualités qui lui permettent d'atteindre les objectifs scientifiques fixés.
Question 1)
Le spectromètre est installé derrière le télescope de 3.6 m de l'ESO. Sa pièce principale, le réseau, présente une hauteur 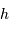 de 20 cm. Déterminer le grossissement
de 20 cm. Déterminer le grossissement 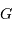 du montage afocal permettant un éclairement optimum du réseau, en supposant un faisceau non divergent.
du montage afocal permettant un éclairement optimum du réseau, en supposant un faisceau non divergent.
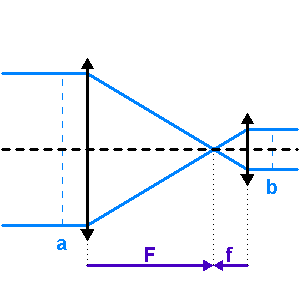
Rappel du montage afocal
Faisceau de sortie du montage afocal
Crédit :
ASM
Question 2)
Montrer qu'une déviation 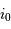 dans le champ objet se traduit par une variation
dans le champ objet se traduit par une variation 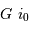 de l'angle dispersé.
de l'angle dispersé.
Relier la déviation de 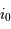 à celle de
à celle de 
Question 3)
Rappeler l'expression donnant les variations 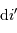 de l'angle de dispersion
de l'angle de dispersion 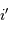 en fonction des variations de longueur d'onde
en fonction des variations de longueur d'onde 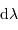 , du pas
, du pas 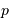 du réseau, et selon l'ordre d'interférence
du réseau, et selon l'ordre d'interférence 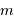 .
.
Le réseau envoie la lumière préférentiellement dans la direction 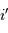 obéissant à :
obéissant à :
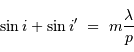
Différencier l'expression précédente.
Question 4)
On cherche à déterminer le champ objet maximal, qui permette
d'atteindre un pouvoir de résolution 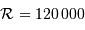 . Montrer que cette performance nécessite un faisceau émergeant du spectromètre de taille angulaire limitée à
. Montrer que cette performance nécessite un faisceau émergeant du spectromètre de taille angulaire limitée à
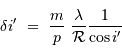
et conclure. On fera l'application numérique avec les données :
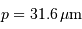 ,
, 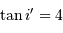 et un ordre d'interférence
et un ordre d'interférence 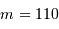 à
à 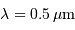 :
:
Question 5)
Justifier a posteriori l'hypothèse de non-divergence du faisceau. On pourra considérer un faisceau optique de longueur 8 m dans l'instrument.
Estimer la divergence en fonction de la longueur 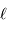 proposée et de l'angle
proposée et de l'angle 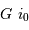 .
.
Plusieurs techniques permettent de réaliser la spectro-imagerie, càd une information spectrales pour plusieurs objets, plusieurs points du champ ou bien tout un champ.
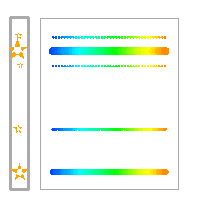
La fente sélectionne les objets du champ. La mosaïque CCD enregistre un spectre de chaque objet du champ.
Crédit :
ASM
Spectrométrie à longue fente
La fente du spectromètre sélectionne les objets du champ. La dispersion, perpendiculaire à la fente, apporte un spectre pour chacun de ses objets .
Découpe d'image
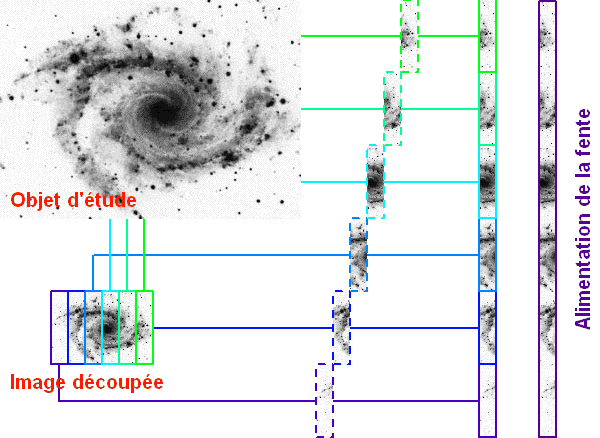
Le découpeur d'image permet, à partir d'une source étendue, d'illuminer la fente du spectromètre. Le champ entier est préservé, à un réarrangement près. Le découpeur correspond simplement à une collage de prismes, avec l'équivalent de 2 prismes croisés par tranche découpée. L'étape intermédiaire (avec les tiretés) a été représentée uniquement à des fins didactiques.
Crédit :
ASM
Découpage d'image
L'image est optiquement découpée en tranches, afin de couvrir la fente d'entrée du spectro. L'analyse des images monochromatiques de la fente d'entrée permettra de reconstituer chacune des régions initiales.
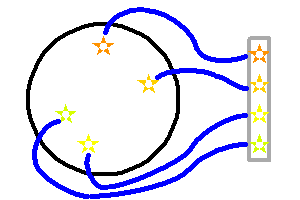
Sélection des objets par le faisceau de fibres, et alimentation de la fente d'entrée.
Crédit :
ASM

Une image intermédiaire est formée au niveau du système ici visualisé. Les têtes de fibre, chacune positionnable à l'extrémité d'un bras mobile, peuvent aller chercher le flux de tout point du champ.
L'instrument doit également fonctionner en imageur, pour repérer très précisément au préalable les positions des objets sélectionnés.
Crédit :
ESO

Les 7 cibles sélectionnés sont 7 galaxies d'un amas : les décalages des spectres donnent la dispersion des vitesses des différentes galaxies.
Crédit :
ESO
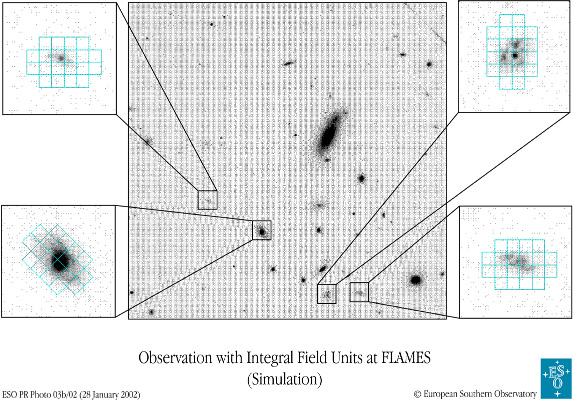
Spectroscopie multi-objet avec l'instrument FLAMES au VLT.
Crédit :
ESO
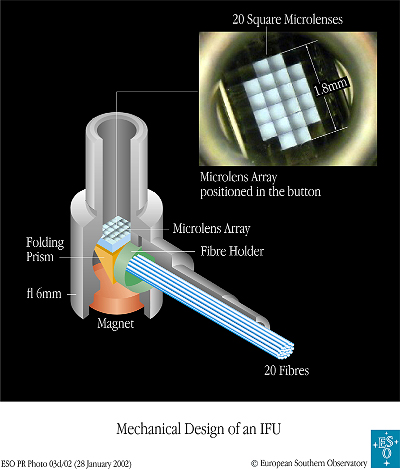
Concept optique pour la spectroscopie multi-objets : les 20 microlentilles irriguent 20 fibres optiques.
Crédit :
ESO
 Définition
Définition
Spectro-imagerie : spectrométrie sur un champ non limité à un seul point source.
Spectrométrie à fente longue
La spectrométrie à fente longue a pour objet l'enregistrement simultané de spectres à basse résolution pour les différentes sources sélectionnées par la fente.
Le flux issu de chaque sous-région de la fente est dispersé. La dispersion étant perpendiculaire à la fente, l'image bidimensionnelle finale résulte du produit de 2 dimensions : l'une est spectrale, l'autre est spatiale.
Spectrométrie multi-objets
La spectrométrie multi-objets réalise l'enregistrement simultané de spectres à basse résolution pour plusieurs régions d'une image.
Les flux de ces régions sont collectés via des fibres, qui organisent une anamorphose de l'image. En entrée, les sources sont réparties indifféremment dans le champ ; en sortie, leurs images par les fibres, sources pour le spectromètre, sont alignées le long de la fente.
Le flux issu de chaque fibre est dispersé. Comme pour la spectrométrie à fente longue, l'image bidimensionnelle finale résulte du produit de 2 dimensions : l'une spectrale, l'autre spatiale. Mais la correspondance entre les pixels et le champ est à considérer selon l'anamorphose effectuée.
Par rapport à la spectrométrie à longue fente, la souplesse des fibres permet de sélectionner plus pertinemment les sources.
Spectrométrie intégrale de champ
La spectrométrie intégrale de champ propose l'enregistrement simultané de spectres à basse résolution de tout un champ objet.
L'objet est découpé en un certain nombre de régions, chacune étant alors considérée comme une source ponctuelle, ensuite dispersée.
L'espace entre les images de chacune de ces sources ponctuelles est suffisant pour permettre d'enregistrer, pour chacune, un spectre à basse résolution.
Spectrométrie multi-objets
La fente du spectromètre UVES de l'ESO, fonctionnant en spectrométrie multi-objets, est illuminée par 8 fibres. Sept d'entre elles visent 7 cibles, la 8ème est réservée à la référence spectrale (une lampe à vapeur spectrale, dont on voit les raies en émission).
Spectrométrie multi-objets 
Spectrométrie intégrale de champ 
Spectrométrie intégrale de champ
La résolution spatiale est dégradée, pour permettre l'enregistrement de spectre sur une grille de régions du champ.
Le réseau de microlentilles découpe le faisceau, et crée autant d'images ponctuelles qu'il y a de microlentilles. Ces images ponctuelles sont ensuite autant de sources pour un spectrographe.
On récupère en sortie un spectre de résolution moyenne pour chaque région de l'objet découpée par la microlentille
(cf instrument CFHT/Observatoire de Lyon).
 Spectrométrie intégrale de champ : résolutions spatiale et spectrale
Spectrométrie intégrale de champ : résolutions spatiale et spectrale
Difficulté : ☆☆
Temps : 20 min
Cet exercice a pour but d'estimer l'ordre de grandeur des performances d'un spectromètre intégral de champ, qui donne des images sur un CCD de 2k  2k (2000 fois 2000 pixels).
On note
2k (2000 fois 2000 pixels).
On note 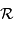 le pouvoir de résolution spectrale visé,
le pouvoir de résolution spectrale visé, 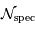 le nombre d'éléments spectraux correspondant,
le nombre d'éléments spectraux correspondant, 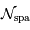 le nombre d'informations spatiales souhaité.
le nombre d'informations spatiales souhaité.
Question 1)
Montrer que, si l'intervalle spectral est large, alors en ordre de grandeur
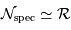 . On se place par la suite dans le cadre de cette hypothèse.
. On se place par la suite dans le cadre de cette hypothèse.
Pour fixer les ordres de grandeur, on peut traduire large intervalle spectral comme 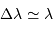 .
.
Les définitions de 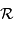 et
et 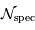 sont :
sont :
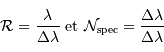
Question 2)
Montrer que le produit 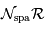 est nécessairement borné.
est nécessairement borné.
Réfléchir à la signification du mot pixel. Combien d'informations spatiales élémentaires un CCD de 2k 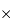 2k peut-il traiter?
2k peut-il traiter?
Question 3)
On considère pour la suite qu'entre le codage, l'étalonnage, la séparation des spectres..., une information élémentaire nécessite 20 pixels.
On souhaite une résolution spectrale de 200. En déduire le nombre d'informations spatiales maximal.
Montrer que, vu les hypothèses :
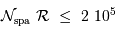
Antenne millimétrique


Réseau des 6 antennes millimétriques de l'observatoire du Pic de Bure de l'
IRAM. L'extension maximale de l'interféromètre atteint 408 m sur la branche Est-Ouest, et 232 m en Nord-Sud.
Crédit :
IRAM
VLA

Réseau d'antenne VLA (Very Large Array) du NRAO (National Radio Astronomy Observatory), travaillant aux longueurs d'onde de 1.2, 2, 6 et 21 cm. 27 antennes sont disposées sur 3 branches en Y, s'étendant sur 19
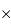
21 km
Crédit :
NRAO
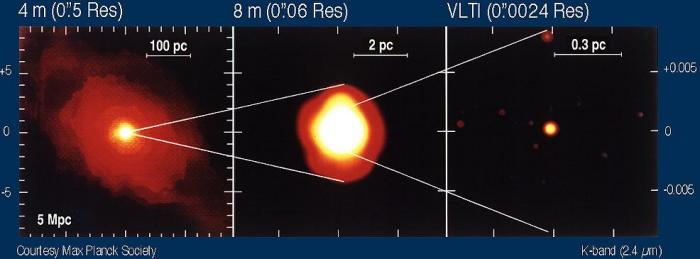
Séquence illustrant le gain en résolution spatiale entre une image non corrigée par optique adaptative, corrigée, ou enregistrée en mode interférométrique.
Crédit :
ESO/Max Planck Society

Les 4 télescopes du VLT. La configuration VLTI, interférométrique, s'obtient en recombinant les faisceaux via les galeries enterrées qui apparaissent sur la photo.
Crédit :
ESO
Ligne à retard du VLTI

Le faisceau issu du collecteur le plus proche de la source doit être rallongé, pour interférer avec l'autre faisceau à différence de marche quasi-nulle. Cela nécessite des lignes à retard de grande longueur (extension maximale de 60 m, pour un retard double après un aller-retour), dans le tunnel interférométrique.
Crédit :
ESO
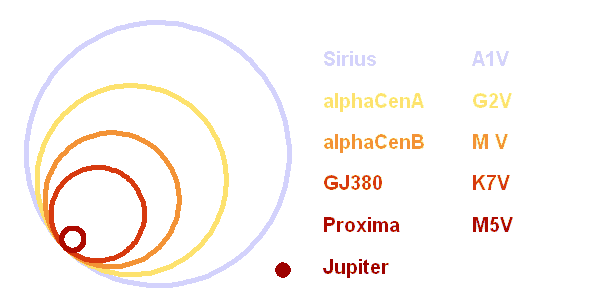
Schéma à l'échelle du rayon de différentes étoiles naines de la séquence principale. Rayons mesurés avec le VLTI.
Crédit :
ASM
Le VLTI
On nomme VLTI la configuration interférométrique des télescopes du VLT. La longueur de cohérence pour une source astronomique étant limitée, l'obtention de franges d'interférence nécessite des lignes à retard pour mélanger les faisceaux des différents collecteurs.
Une des premières opérations du VLTI a consisté en la mesure de diamètres stellaires d'étoiles de la séquence principale. La mesure de ces diamètres angulaires est impossible sans la haute résolution apportée par l'interférométrie.
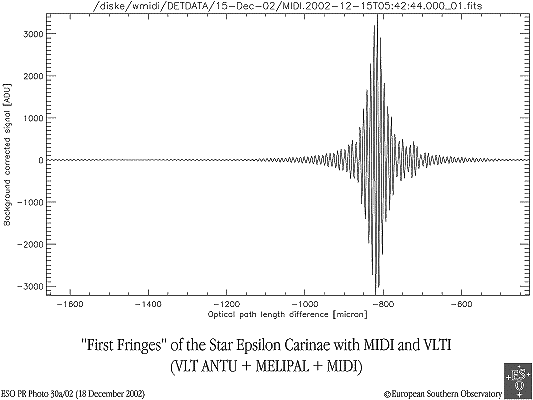
Enregistrement de franges d'interférence. La cohérence spatiale est limitée par la taille angulaire de la source.
Crédit :
ESO
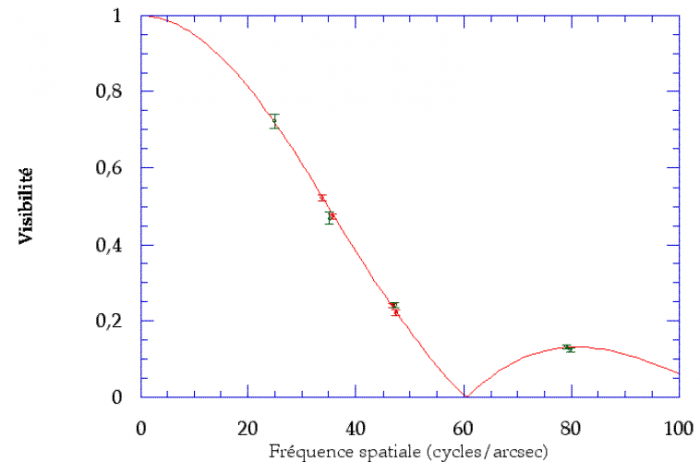
La mesure du diamètre angulaire de l'étoile
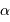
du Bouvier (Arcturus) résulte de la visibilité des franges d'interférence obtenues par interférométrie.
Crédit :
ESO
 Objectifs
Objectifs
Augmenter la résolution angulaire, ultimement limitée par la diffraction d'un collecteur, en faisant interférer les faisceaux de plusieurs collecteurs.
 Prérequis
Prérequis
Diffraction, interférence ; la notion de cohérence spatiale est nécessaire pour justifier les techniques d'interférométrie.
Recombinaison
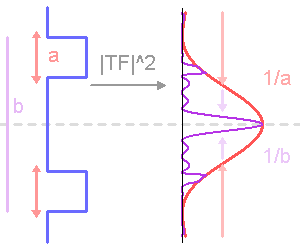
La tache de diffraction d'un seul télescope de diamètre collecteur
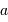
est en
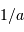
; la tache image résultant de l'interférence sur la base
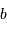
est en
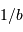
.
Crédit :
ASM
Configuration de Fizeau
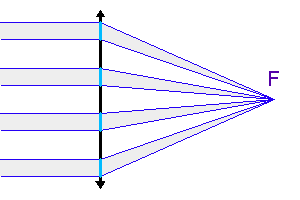
Interféromètre dans la configuration de Fizeau. Les différentes surfaces collectrices sont des sous-parties d'une unique surface. Les faisceau convergent en phase au foyer commun.
Crédit :
ASM
Configuration de Michelson
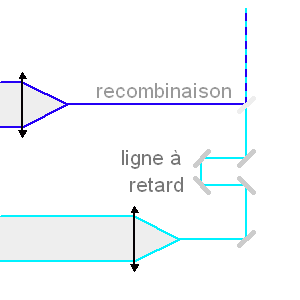
Interféromètre dans la configuration de Michelson. Une ligne à retard doit assurer le cophasage des faisceaux recombinés.
Crédit :
ASM
Le principe
Les faisceaux issus de 2 collecteurs pointant le même objet sont recombinés, de manière cohérente, pour interférer.
Exemple de valeur numérique : dans le proche infrarouge, pour une base de 100 m :
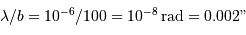 .
.
Exemple de recombinaison : interféromètre de type Michelson, ou bien Fizeau. Dans ce dernier cas, les surfaces collectrices sont des éléments disjoints d'une surface collectrice unique.
Vers la haute résolution angulaire
L'interférométrie s'est développée dans un premier temps dans le domaine radio. Dans ce domaine de fréquence, la détection cohérente permet une recombinaison du signal plus aisément qu'aux fréquences optiques. La phase du signal étant enregistrée, cette recombinaison n'a même pas à être nécessairement menée en temps réel.
L'interférométrie dans le domaine des grandes longueurs d'onde apparaît par ailleurs le plus souvent indispensable, la taille de la tache de diffraction dans ce domaine conduisant, malgré les grands diamètres collecteurs, à une résolution angulaire médiocre.
L'interférométrie est aujourd'hui développée jusque dans le domaine visible : en l'absence de pupille de grande taille, c'est la seule technique donnant accès à la haute résolution angulaire.
Technique d'observation
On s'intéresse aux interférences construites entre paires de collecteurs. Le problème se ramène à une situation de type trous d'Young, avec l'analogie entre les trous d'Young et les collecteurs.
La longueur de cohérence du faisceau stellaire est limitée. Réaliser des interférences ne se limite pas à une sommation des intensités lumineuses : observer des franges d'interférence nécessite d'égaler les chemins optiques des 2 voies à quelques longueurs d'onde près avant leur recombinaison.
Des lignes à retard optiques permettent de réaliser ceci.
De la même façon que le paramètre pertinent pour visualiser les franges d'interférences issus des trous d'Young est l'écart angulaire 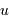 par rapport à l'image géométrique, il est utile de faire la correspondance entre la projection des lignes de bases de l'interféromètre, projetées sur le plan d'onde. Une configuration donnée, à une date donnée, va conduire à la mesure de la visibilité des franges d'interférences pour un vecteur angulaire donné
par rapport à l'image géométrique, il est utile de faire la correspondance entre la projection des lignes de bases de l'interféromètre, projetées sur le plan d'onde. Une configuration donnée, à une date donnée, va conduire à la mesure de la visibilité des franges d'interférences pour un vecteur angulaire donné 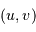 .
.
La courbe de visibilité dépend de la taille angulaire de la source, dès lors que celle-ci est résolue par l'interféromètre. Plus la source sera étendue, plus les franges d'interférence apparaîtront brouillées dès lors que l'on s'éloigne angulairement de la direction de l'optique géométrique.
Base
La ligne de base correspond à la projection sur le plan du ciel, donc orthogonale à la ligne de visée, de la position des télescopes.
Du fait de la rotation de la Terre, elle varie au cours de l'observation.
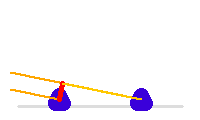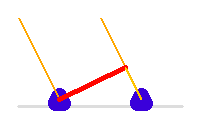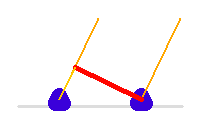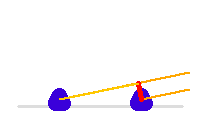
La ligne de base, en rouge, varie en cours de la nuit. Le trajet supplémentaire de la lumière sur l'un des voies est à compenser par une ligne à retard.
Crédit :
ASM
Synthèse d'ouverture
Les animations ci-jointes montrent comment évoluent, au cours d'une séquence d'observation, les lignes de base d'un site avec 3 télescopes interférant, avec les fréquences spatiales sur le plan du ciel.
Si l'objet ne varie pas rapidement dans le temps, il est possible de prendre le temps de nombreuses configurations interférométriques, au besoin avec des changements de positions des télescopes (lorsque cela est possible), pour reconstituer suffisamment de fréquences spatiales et imager en détail l'objet.
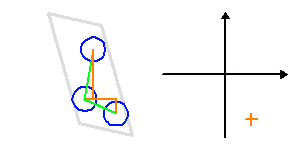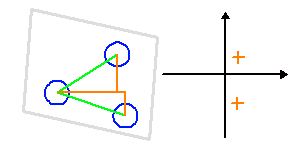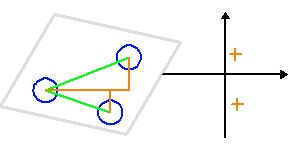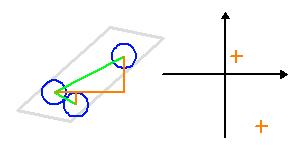
Au cours d'une nuit d'observation, une source donnée voit le plan de 3 télescopes d'un interféromètre sous un angle variable. A 3, ils construisent 2 lignes de base indépendantes, et donnent accès à 2 fréquences spatiales différentes (croix orange).
Crédit :
ASM
 QCM
QCM
 L'interféromètre du plateau de Bure
L'interféromètre du plateau de Bure
Difficulté : ☆
Temps : 10 min
Les antennes de l'IRAM du plateau de Bure ont un diamètre de 15 m.
Question 1)
Déterminer la tache d'Airy, pour une observation menée à 230 GHz.
Une fréquence de 230 GHz correspond à une longueur d'onde de 1.3 mm.
Question 2)
Que devient cette résolution pour une observation interférométrique avec une ligne de base de 400 m ?
Déterminer le gain en éléments de résolution sur un objet.
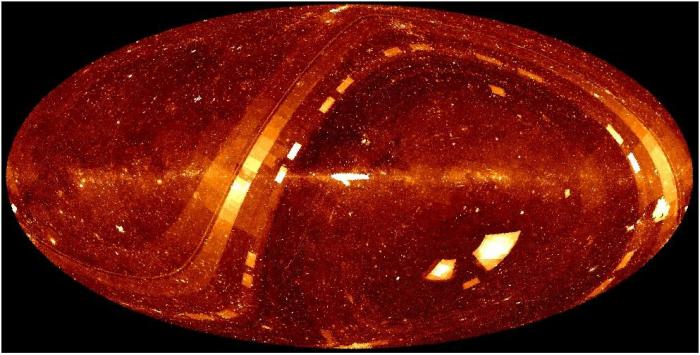
Carte du ciel en coordonnées galactiques, avec représentation de la densité des régions les plus étudiées et accessible dans le catalogue Vizir tenu par le Centre de Données Stellaires de l'Observatoire de Strasbourg.
Crédit :
CDS
Catalogues
Les différents programmes d'observations des différents télescopes ont conduit à l'accumulation de très nombreuses données, compilées dans de non moins nombreux catalogues. Aujourd'hui, soit ces catalogues sont devenus obsolètes, soit ils sont accessibles en ligne pour être accessibles, pour profiter à la plus large communauté, pour être intercroisés avec d'autres observations...

C'est par comparaison avec une image d'archive que peut être mis en évidence un événement tel une supernova.
Crédit :
ESO
Exemple d'intérêt : archive
Un intérêt majeur d'un observatoire virtuel consiste à fournir des archives, p.ex. pour détecter un phénomène nouveau, tel l'apparition d'une supernova.
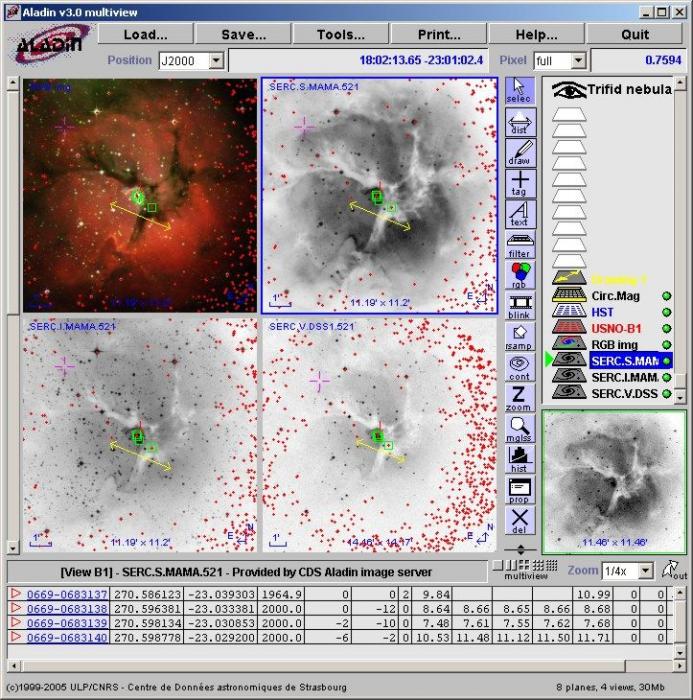
Aperçu d'un outil permettant de comparer des clichés dûment catalogués d'un même objet à différentes longueurs d'onde.
Crédit :
CDS
Exemple d'intérêt : analyse multispectrale
Approche
multispectrale de M20 proposée par le Centre de Données Stellaires de l'Observatoire de Strasbourg. Les outils permettent de retrouver des informations, les comparer...
 Définition
Définition
Un observatoire virtuel correspond à un centre de données, donnant accès à des observations passées classées, archivées, ainsi que des outils spécifiquement développés pour travailler ces observations.
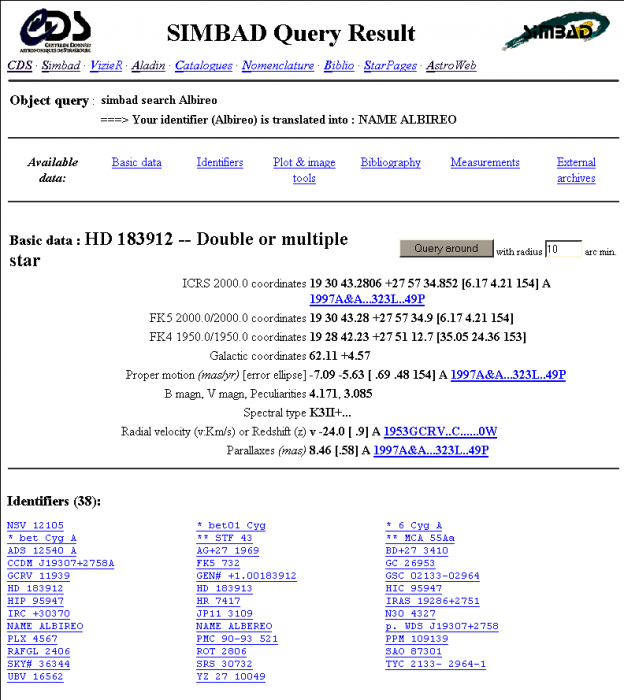
Une page, parmi tant d'autres, de la base de donnée SIMBAD. Renseignements sur une cible donnée : coordonnées, articles de référence, et liens vers ses multiples dénominations, différant les unes des autres selon le catalogue d'observation.
Crédit :
CDS
Base de données
Les évolutions technologies ne permettent pas seulement d'avoir des instruments plus performants, pilotés par des interfaces efficaces. Elles ouvrent aussi la possibilité de mettre à la disposition de la communauté des chercheurs les observations menées par les différents programmes.
Les bases de données
classent et organisent dans des formats facilement portables les résultats obtenus par les grands observatoires, leurs programmes majeurs d'atlas et d'observation de régions précises, les missions spatiales...
Vers les observatoires virtuels
Un observatoire virtuel, c'est une base de données suffisamment bien achalandée, organisée et agencée pour permettre non de réaliser une observation, mais d'accéder à des observations passées susceptibles de fournir les renseignements cherchés.
Un observatoire virtuel doit ainsi permettre :
- de comparer des observations concernant un même objet,
- de comparer des observations obtenues à des dates différentes,
- de croiser des observations obtenues à des longueurs d'onde différentes...
Pour en savoir plus, voir p.ex. le site du Centre de Données astronomiques de Strasbourg (CDS).
Cette section a exposé les principales mises en forme du signal astronomique. Chacune correspond à une instrumentation spécifique.
Une bonne part de la recherche astrophysique concerne le développement d'instruments encore plus puissants, efficaces, sensibles, précis, stables... sachant qu'il est impossible de tout faire simultanément.

Instrument AMBER, spectromètre du VLTI observant dans le proche infrarouge avec un pouvoir de résolution pouvant monter jusqu'à 10 000.
Crédit :
ESO
- Question 1
Aide :
Rappel du montage afocal
Faisceau de sortie du montage afocal

Crédit :
ASM
Solution :
Le grossissement du télescope doit transformer un faisceau parallèle de diamètre 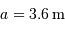 en un autre faisceau parallèle de diamètre
en un autre faisceau parallèle de diamètre 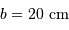 . Le grossissement doit donc vérifier :
. Le grossissement doit donc vérifier :
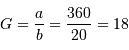
- Question 2
Aide :
Relier la déviation de 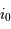 à celle de
à celle de 
Solution :
Vu le grossissement,
une déviation 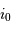 dans le champ objet se traduit par une variation
dans le champ objet se traduit par une variation 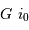 dans le champ image. Le spectromètre, attaqué par une onde incidente déviée, renvoie la lumière dans une direction déviée d'autant. On retrouve donc pour
dans le champ image. Le spectromètre, attaqué par une onde incidente déviée, renvoie la lumière dans une direction déviée d'autant. On retrouve donc pour 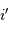 cette déviation
cette déviation 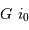 .
.
- Question 3
Aide :
Le réseau envoie la lumière préférentiellement dans la direction 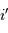 obéissant à :
obéissant à :
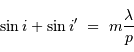
Aide :
Différencier l'expression précédente.
Solution :
Le réseau envoie la lumière préférentiellement dans la direction 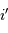 obéissant à :
obéissant à :
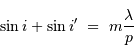
A incidence  fixée, la différentiation de la relation précédente donne :
fixée, la différentiation de la relation précédente donne :
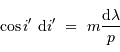
D'où la relation de dispersion :
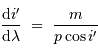
- Question 4
Aide :
Faire le lien entre 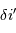 ,
, 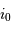 et le grossissement
et le grossissement 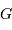 .
.
Solution :
La dispersion du réseau énonce :
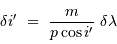
La résolution souhaitée entraîne la nécessité de distinguer des éléments spectraux de largeur :
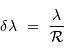
Par ailleurs, des variations de l'angle d'injection 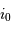 se traduisent par des variations de
se traduisent par des variations de 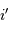 à hauteur de
à hauteur de 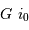 . On en déduit que les variations de l'angle
. On en déduit que les variations de l'angle 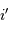 doivent être contraintes par :
doivent être contraintes par :
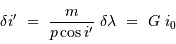
Et donc 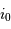 doit satisfaire :
doit satisfaire :
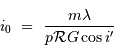
L'application numérique donne (avec 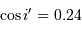 ) :
) :

On en déduit que le champ objet doit être extrêmement réduit. La fibre du spectromètre HARPS sélectionne ainsi uniquement 1" sur le ciel.
- Question 5
Aide :
Estimer la divergence en fonction de la longueur 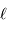 proposée et de l'angle
proposée et de l'angle 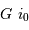 .
.
Solution :
Une déviation angulaire 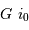 avec un bras de levier de longueur
avec un bras de levier de longueur 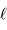 se traduit par une déviation linéaire
se traduit par une déviation linéaire 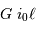 .
.
L'application numérique donne 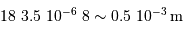 . Ces 0.5 mm sont totalement négligeables devant la hauteur du faisceau de 20 cm.
. Ces 0.5 mm sont totalement négligeables devant la hauteur du faisceau de 20 cm.
- Question 1
Aide :
Pour fixer les ordres de grandeur, on peut traduire large intervalle spectral comme 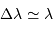 .
.
Aide :
Les définitions de 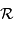 et
et 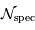 sont :
sont :
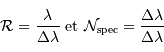
Solution :
En supposant 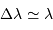 , on vérifie bien que
, on vérifie bien que
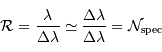
- Question 2
Aide :
Réfléchir à la signification du mot pixel. Combien d'informations spatiales élémentaires un CCD de 2k  2k peut-il traiter?
2k peut-il traiter?
Solution :
En supposant un rendement optimal, le nombre de pixels fournit le nombre d'éléments spectraux et spatiaux. Au mieux, pour un détecteur 2k  2k :
2k :
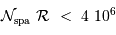
Mais comme on va souhaiter échantillonner une information spatiale ou spectrale sur au moins 2 pixels, et qu'il est prudent de laisser des pixels non éclairés entre chaque spectre, il faut plutôt compter :
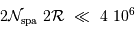
- Question 3
Aide :
Montrer que, vu les hypothèses :
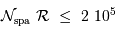
Solution :
Avec 20 pixels par information élémentaire, on a :
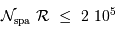
L'application numérique donne un nombre d'informations spatiales indépendantes 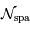 limité à :
limité à :
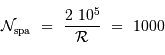
Le nombre de pixels étant limité, on ne peut pas simultanément gagner en résolutions spatiale et spectrale.







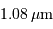 . Ce domaine spectral est sélectionné par un filtre étroit. Noter l'unité spectrale, inverse de la longueur d'onde.
. Ce domaine spectral est sélectionné par un filtre étroit. Noter l'unité spectrale, inverse de la longueur d'onde.





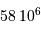
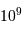
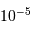

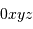 telle que le plan
telle que le plan 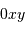 corresponde au miroir primaire de la
détection. La quantité de mouvement du photon incident est
quasiment parallèle à
corresponde au miroir primaire de la
détection. La quantité de mouvement du photon incident est
quasiment parallèle à 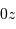 . On suppose que la formation d'image
suit parfaitement les lois de l'optique géométrique.
. On suppose que la formation d'image
suit parfaitement les lois de l'optique géométrique.
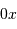 .
Peut-on connaître la position de l'impact et de la réflexion du
photon sur le miroir? En déduire que le front d'onde incident est
découpé en tranche de largeur la dimension du miroir, que la
position selon l'axe
.
Peut-on connaître la position de l'impact et de la réflexion du
photon sur le miroir? En déduire que le front d'onde incident est
découpé en tranche de largeur la dimension du miroir, que la
position selon l'axe 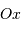 est inconnue, et que donc elle est
affublée d'une incertitude de position
est inconnue, et que donc elle est
affublée d'une incertitude de position 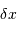 .
.
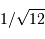 . En déduire
l'incertitude de mesure de la composant selon
. En déduire
l'incertitude de mesure de la composant selon 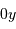 de la quantité
de mouvement du photon.
de la quantité
de mouvement du photon.
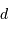 .
.
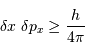
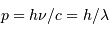 .
En déduire que l'incertitude de repérage de l'angle d'incidence du
photon vaut :
.
En déduire que l'incertitude de repérage de l'angle d'incidence du
photon vaut :
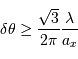
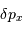 .
.
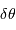 en fonction de
en fonction de 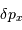 .
.
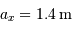 . Cela est-il
compatible avec les performances annoncées, de l'ordre de
. Cela est-il
compatible avec les performances annoncées, de l'ordre de 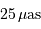 à la magnitude
à la magnitude 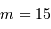 ? Pourquoi ?
? Pourquoi ?
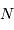 photons effectivement
détectés, l'incertitude est divisée par
photons effectivement
détectés, l'incertitude est divisée par 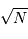 . Combien de
photons doivent être détectés pour aboutir à la performance
annoncée.
. Combien de
photons doivent être détectés pour aboutir à la performance
annoncée.







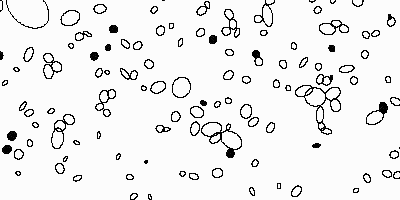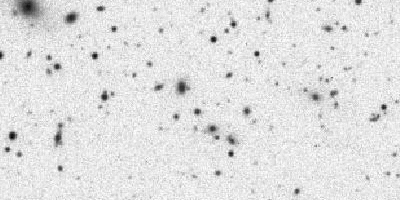



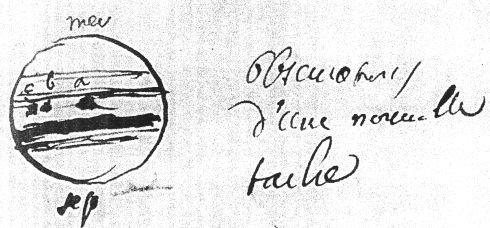

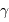 , la capacité d'imagerie des détecteurs est très limitée, et il est souvent difficile de bien localiser une source même intense. Du côté des très grandes longueurs d'onde, la tache d'Airy due à la diffraction peut atteindre une extension angulaire très grande ce qui limite la résolution spatiale.
, la capacité d'imagerie des détecteurs est très limitée, et il est souvent difficile de bien localiser une source même intense. Du côté des très grandes longueurs d'onde, la tache d'Airy due à la diffraction peut atteindre une extension angulaire très grande ce qui limite la résolution spatiale.


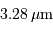 , alors que Io apparaît bien plus brillant à cette longueur d'onde.
, alors que Io apparaît bien plus brillant à cette longueur d'onde.


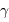 , X, visible, proche, moyen et lointain infrarouge, raie de
, X, visible, proche, moyen et lointain infrarouge, raie de 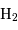 , H atomique, et radio.
, H atomique, et radio.






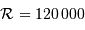 , en proposant une excellente stabilité. Les mesures sont stables et reproductibles, sur une durée de plusieurs années, à mieux que le milliardième près. Les spectres de HARPS sont obtenus avec les différents ordres d'interférences repliés sur une
, en proposant une excellente stabilité. Les mesures sont stables et reproductibles, sur une durée de plusieurs années, à mieux que le milliardième près. Les spectres de HARPS sont obtenus avec les différents ordres d'interférences repliés sur une 
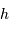 de 20 cm. Déterminer le grossissement
de 20 cm. Déterminer le grossissement 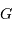 du montage afocal permettant un éclairement optimum du réseau, en supposant un faisceau non divergent.
du montage afocal permettant un éclairement optimum du réseau, en supposant un faisceau non divergent.

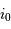 dans le champ objet se traduit par une variation
dans le champ objet se traduit par une variation 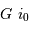 de l'angle dispersé.
de l'angle dispersé.
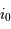 à celle de
à celle de 
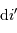 de l'angle de dispersion
de l'angle de dispersion 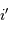 en fonction des variations de longueur d'onde
en fonction des variations de longueur d'onde 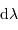 , du pas
, du pas 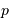 du réseau, et selon l'ordre d'interférence
du réseau, et selon l'ordre d'interférence 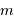 .
.
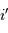 obéissant à :
obéissant à :
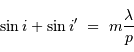
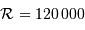 . Montrer que cette performance nécessite un faisceau émergeant du spectromètre de taille angulaire limitée à
. Montrer que cette performance nécessite un faisceau émergeant du spectromètre de taille angulaire limitée à
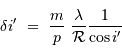
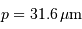 ,
, 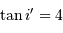 et un ordre d'interférence
et un ordre d'interférence 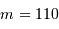 à
à 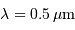 :
:
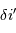 ,
, 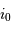 et le grossissement
et le grossissement 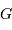 .
.
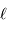 proposée et de l'angle
proposée et de l'angle 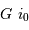 .
.







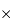 2k (2000 fois 2000 pixels).
On note
2k (2000 fois 2000 pixels).
On note 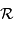 le pouvoir de résolution spectrale visé,
le pouvoir de résolution spectrale visé, 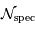 le nombre d'éléments spectraux correspondant,
le nombre d'éléments spectraux correspondant, 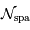 le nombre d'informations spatiales souhaité.
le nombre d'informations spatiales souhaité.
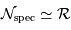 . On se place par la suite dans le cadre de cette hypothèse.
. On se place par la suite dans le cadre de cette hypothèse.
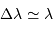 .
.
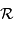 et
et 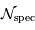 sont :
sont :
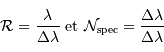
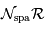 est nécessairement borné.
est nécessairement borné.
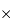 2k peut-il traiter?
2k peut-il traiter?
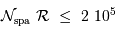



 21 km
21 km






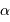 du Bouvier (Arcturus) résulte de la visibilité des franges d'interférence obtenues par interférométrie.
du Bouvier (Arcturus) résulte de la visibilité des franges d'interférence obtenues par interférométrie.

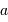 est en
est en 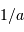 ; la tache image résultant de l'interférence sur la base
; la tache image résultant de l'interférence sur la base 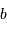 est en
est en 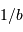 .
.


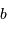 , la résolution angulaire de la tache image des faisceaux interférant à la longueur d'onde
, la résolution angulaire de la tache image des faisceaux interférant à la longueur d'onde 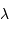 vaut
vaut 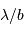 .
.
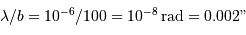 .
.
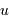 par rapport à l'image géométrique, il est utile de faire la correspondance entre la projection des lignes de bases de l'interféromètre, projetées sur le plan d'onde. Une configuration donnée, à une date donnée, va conduire à la mesure de la visibilité des franges d'interférences pour un vecteur angulaire donné
par rapport à l'image géométrique, il est utile de faire la correspondance entre la projection des lignes de bases de l'interféromètre, projetées sur le plan d'onde. Une configuration donnée, à une date donnée, va conduire à la mesure de la visibilité des franges d'interférences pour un vecteur angulaire donné 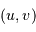 .
.


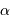 -Cen, située à 4.2 AL du Soleil, de rayon linéaire voisin de celui du soleil (750 000 km)?
-Cen, située à 4.2 AL du Soleil, de rayon linéaire voisin de celui du soleil (750 000 km)?
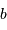 est nécessaire pour mesurer le diamètre d'une étoile de type analogue à
est nécessaire pour mesurer le diamètre d'une étoile de type analogue à 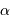 -Cen mais située à 10 pc, en faisant la mesure à une longueur d'onde de 1 micron ?
-Cen mais située à 10 pc, en faisant la mesure à une longueur d'onde de 1 micron ?
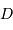 sur une base
sur une base 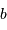 est définie par :
est définie par :





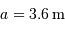 en un autre faisceau parallèle de diamètre
en un autre faisceau parallèle de diamètre 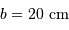 . Le grossissement doit donc vérifier :
. Le grossissement doit donc vérifier :
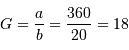
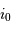 dans le champ objet se traduit par une variation
dans le champ objet se traduit par une variation 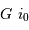 dans le champ image. Le spectromètre, attaqué par une onde incidente déviée, renvoie la lumière dans une direction déviée d'autant. On retrouve donc pour
dans le champ image. Le spectromètre, attaqué par une onde incidente déviée, renvoie la lumière dans une direction déviée d'autant. On retrouve donc pour 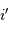 cette déviation
cette déviation 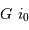 .
.
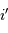 obéissant à :
obéissant à :
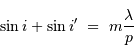
 fixée, la différentiation de la relation précédente donne :
fixée, la différentiation de la relation précédente donne :
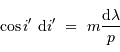
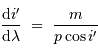
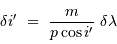
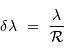
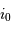 se traduisent par des variations de
se traduisent par des variations de 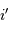 à hauteur de
à hauteur de 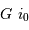 . On en déduit que les variations de l'angle
. On en déduit que les variations de l'angle 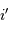 doivent être contraintes par :
doivent être contraintes par :
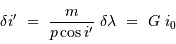
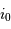 doit satisfaire :
doit satisfaire :
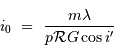
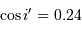 ) :
) :

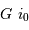 avec un bras de levier de longueur
avec un bras de levier de longueur 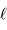 se traduit par une déviation linéaire
se traduit par une déviation linéaire 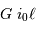 .
.
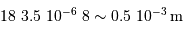 . Ces 0.5 mm sont totalement négligeables devant la hauteur du faisceau de 20 cm.
. Ces 0.5 mm sont totalement négligeables devant la hauteur du faisceau de 20 cm.
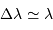 , on vérifie bien que
, on vérifie bien que
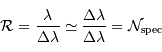
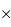 2k :
2k :
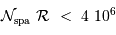
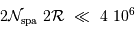
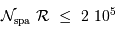
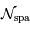 limité à :
limité à :
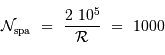
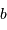 :
:
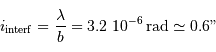
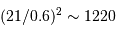 dans le second.
dans le second.