Un spectromètre par transformée de Fourier ne décrit pas directement les raies d'un spectre, mais les fréquence spatiales qui transcrivent ces raies, dans un interférogramme. Il réalise physiquement une opération équivalente à une transformation de Fourier ; l'interférogramme donne ensuite la mesure du spectre par une transformation de Fourier inverse, calculée.
Un spectromètre par transformée de Fourier est un instrument basé sur un interféromètre de Michelson.
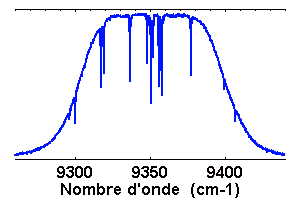
Spectre de Procyon dans le proche infrarouge, aux alentours de
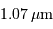
obtenu avec un FTS (Fourier Transform Spectrometer).
Crédit :
ASM

Spectromètre par transformée de Fourier, dans sa cuve à vide, au
foyer Cassegrain du télescope CFH.
Crédit :
CFH
Montage optique
Un spectromètre par transformée de Fourier correspond à un interféromètre de Michelson réglé en anneau : les 2 miroirs sont, à une image via la séparatrice près, parallèles, séparés de la différence de marche.
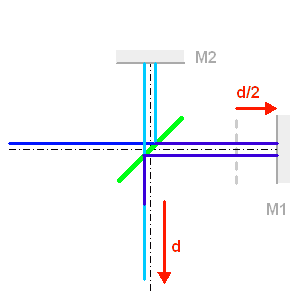
Un décalage de
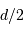
du miroir M1 par rapport à la position équilibrée conduit à une différence de marche
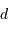
entre les 2 faisceaux recombinés par la lame séparatrice (en vert).
Crédit :
ASM
Les interférences sont localisées à l'infini. Les voir nécessite de regarder à l'infini, p.ex. au foyer d'une lentille.
 Prérequis
Prérequis
Principe de l'interféromètre de Michelson ; transformation de Fourier.
 Objectifs
Objectifs
Expliciter en quoi un interféromètre est dit de Fourier.
Interférences à 2 ondes
On note 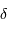 la différence de marche entre les 2 faisceaux monochromatiques interférant à l'infini, et
la différence de marche entre les 2 faisceaux monochromatiques interférant à l'infini, et 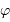 le déphasage. La relation entre
le déphasage. La relation entre 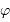 et
et 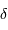 s'exprime, à la longueur d'onde
s'exprime, à la longueur d'onde 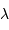 :
:
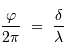
On notera par la suite, en fonction du nombre d'onde :
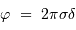
Issus de la même source, ces faisceaux sont cohérents, et leurs amplitudes
vont s'additionner. En notation complexe :
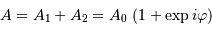
Interférogramme
L'intensité diffractée, pour une différence de marche 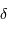 entre les 2 miroirs, sur l'axe, càd dans l'anneau central, constitue l'interférogramme.
En lumière monochromatique de nombre d'onde
entre les 2 miroirs, sur l'axe, càd dans l'anneau central, constitue l'interférogramme.
En lumière monochromatique de nombre d'onde 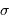 , le signal d'interférence s'écrit à la différence de marche
, le signal d'interférence s'écrit à la différence de marche 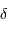 :
:
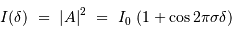
Les unités couramment employées sont, pour le spectre, les nombres d'onde, comptés en 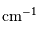 et la différence de marche, comptée en cm.
La période spatiale de l'interférogramme est
et la différence de marche, comptée en cm.
La période spatiale de l'interférogramme est 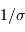 , soit tout simplement la longueur d'onde
, soit tout simplement la longueur d'onde 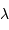 .
.
Interférences et transformée de Fourier
Pour une source non-monochromatique de densité spectrale 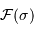 , dans la bande spectrale
, dans la bande spectrale ![[\sigma_1, \ \sigma_2]](../pages_fourier/equations_fts-instrumentation/equation19.png) ,
l'interférogramme prend la valeur :
,
l'interférogramme prend la valeur :
![I(\delta) \ = \ \int_{\sigma_1}^{\sigma_2} { \mathcal{F}}(\sigma) \ \Bigl[ 1 +\cos 2\pi \sigma \delta\Bigr] \ {\mathrm{d}} \sigma](../pages_fourier/equations_fts-instrumentation/equation20.png)
Sans cohérence temporelle
entre les différentes couleurs, il y a sommation des intensités
spectrales 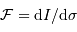 .
La partie modulée (càd qui dépend de la différence de marche
.
La partie modulée (càd qui dépend de la différence de marche 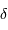 ) de l'interférogramme, correspond à la partie réelle de la TF de la densité spectrale :
) de l'interférogramme, correspond à la partie réelle de la TF de la densité spectrale :
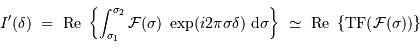
En fait, l'interférogramme réalise la TF de la distribution spectrale de la source. Il s'ensuit que la TF inverse de l'interférogramme permet de remonter au spectre :
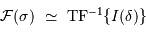
Cette dernière étape est réalisée par calcul (et l'essor des spectromètres par transformée de Fourier a accompagné celui des ordinateurs).
Le principe instrumental
Un spectromètre par transformée de Fourier comprend un interféromètre à 2 ondes, de type interféromètre de Michelson.
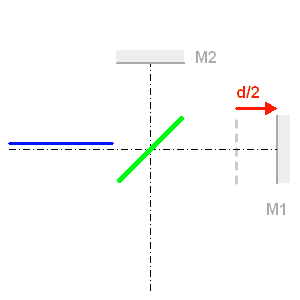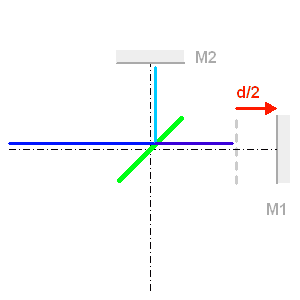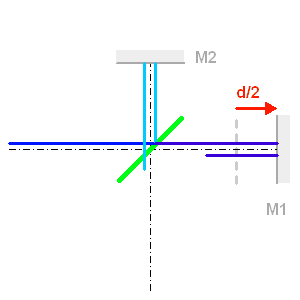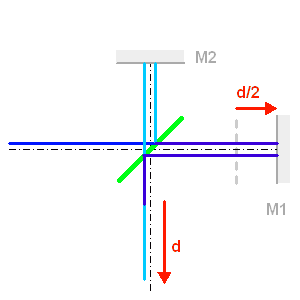
Le FTS dans un monde où la vitesse de la lumière vaut quelques pixels par seconde. La lame semi-réfléchissante sépare les faisceaux. Celui réfléchi sur le miroir mobile est retardé, et lors de la recombinaison sur la lame semi-réfléchissante apparaît une différence de marche entre les 2 faisceaux.
Crédit :
ASM
L'instrument
FTS du CFHT 
L'appliquette ad-hoc décrit le FTS (Fourier Transform Spectrometer) du télescope CFH.
L'interféromètre est de type Mach-Zehnder, plus efficace que l'interféromètre de Michelson car il peut récupérer, sur 2 voies en opposition de phase, 2 interférogrammes : la totalité des photons émis est ainsi utilisée (aux réflexions et transmissions près), contrairement à l'interféromètre de Michelson qui renvoie la moitié des photons vers la source.

Spectre de Procyon dans le proche infrarouge, aux alentours de
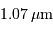
obtenu avec le FTS (Fourier Transform Spectrometer) du télescope CFH.
Crédit :
ASM
Des motifs d'interférence se retrouvent à diverses différences de marche. A grande différence de marche, l'interférogramme est dominé par le bruit de photons.
Crédit :
ASM
Filtre
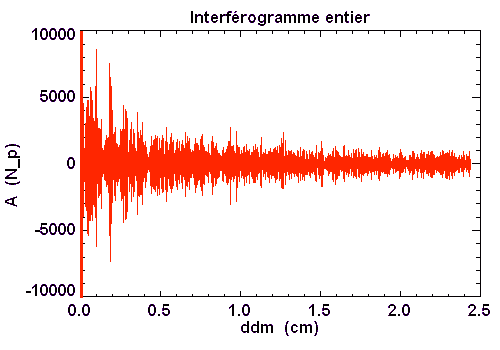
Un filtre est nécessaire pour sélectionner une bande passante limitée du spectre étudié. L'interférogramme associé à cet exemple va comprendre des motifs liés au signal spectral dans le filtre.
Le contraste du signal chute rapidement dès lors que la différence de marche n'est plus nulle.
Crédit :
ASM
Interférogramme proche de la différence de marche nulle
Au proche voisinage de la différence de marche nulle, les franges restent bien contrastées. Le contraste des franges baisse rapidement au fur et à mesure de l'éloignement de la différence de marche nulle.
Interférogramme complet
L'interférogramme complet comprend divers motifs, construits selon les interférences entre les raies sélectionnées par le filtre.
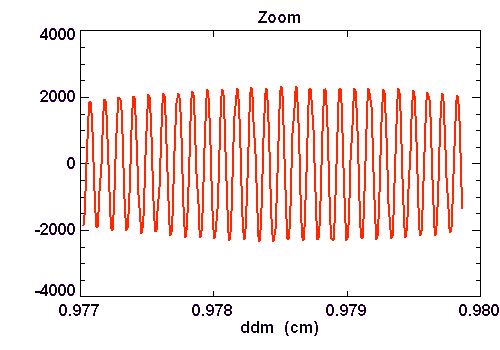
Zoom sur un motif de l'interférogramme.
Crédit :
ASM
Zoom dans l'interférogramme
La visualisation d'un train de franges de l'interférogramme montre une belle portion de sinusoïde modulée par l'enveloppe du train de franges.
 Objectifs
Objectifs
Décrire l'allure de l'interférogramme.
Le spectre théorique initial
Le spectre comprend les données en entrée :
- L'intensité spectrale
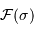 .
. - L'unité
spectrale employée est le nombre d'onde,
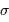 , exprimé en
, exprimé en
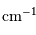 .
.
L'avantage de travailler avec une telle unité spectrale est d'avoir des
variables directement conjuguées entre le spectre et l'interférogramme :
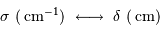
Ces unités employées, quoique hors SI, présentent l'avantage d'être inverses l'une de l'autre.
Interférogramme et TF
L'interférogramme calculé représente la quantité :
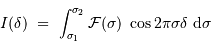
où l'on reconnaît la partie réelle de la TF de la densité
spectrale 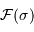 .
.
L'interférogramme réalise physiquement la TF de la distribution spectrale de la source.
La TF inverse de l'interférogramme, calculée, permet de remonter au spectre.
Etendue de faisceau
L'interféromètre étant réglé en anneaux, le principe instrumental ne nécessite pas l'introduction d'une fente d'entrée, contrairement à un spectromètre à réseau.
L'étendue de faisceau n'est donc pas drastiquement limitée par une fente ;
en pratique, elle est limitée par la nécessité de travailler dans un coeur de frange.
Ceci est convenablement dimensionné dans un exercice.
Le signal sur l'axe
L'animation ci-jointe montre comme évolue l'interférogramme en fonction de la différence de marche, pour une onde strictement monochromatique.
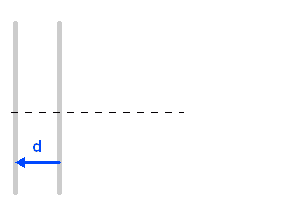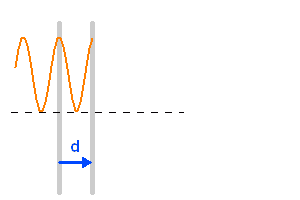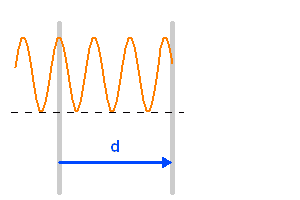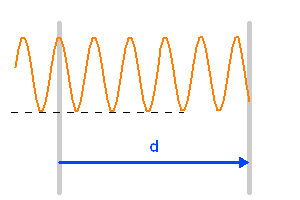
En ramenant optiquement les 2 miroirs sur l'axe, on peut représenter directement la différence de marche, et en déduire le signal oscillant pour une source monochromatique.
Crédit :
ASM
Les anneaux
Les miroirs étant parallèles, les franges d'interférence présentent la symétrie de révolution autour de l'axe optique ; ce sont des
anneaux. On remarque que, par stationnarité de la différence de marche 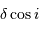 , avec
, avec  l'inclinaison, autour de l'inclinaison nulle, la tache centrale est relativement plus large que les autres anneaux.
l'inclinaison, autour de l'inclinaison nulle, la tache centrale est relativement plus large que les autres anneaux.
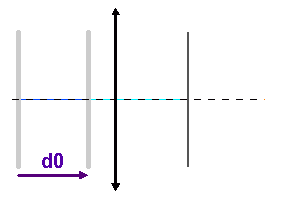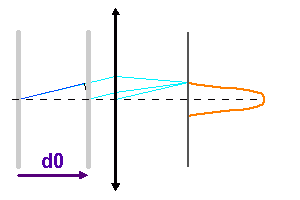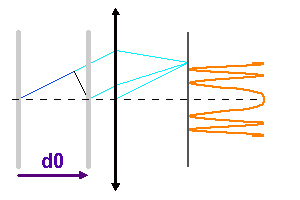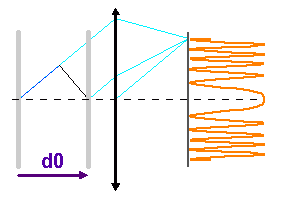
Construction des anneaux d'interférence, pour des inclinaisons importantes sur l'axe.
Crédit :
ASM
 Interférogramme d'un doublet
Interférogramme d'un doublet
Difficulté : ☆☆
Temps : 30 min
On illumine un interféromètre de Fourier avec une source ponctuelle présentant un doublet, aux nombres d'onde 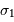 et
et 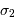 voisins. Chacune des raies est supposée monochromatique, et leurs intensités égales.
voisins. Chacune des raies est supposée monochromatique, et leurs intensités égales.
Question 1)
Déterminer l'expression de l'interférogramme 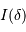 . Mettre en
évidence deux périodes caractéristiques de l'interférogramme.
. Mettre en
évidence deux périodes caractéristiques de l'interférogramme.
Les 2 ondes peuvent-elles être cohérentes ?
On rappelle :
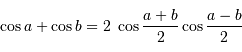
Question 2)
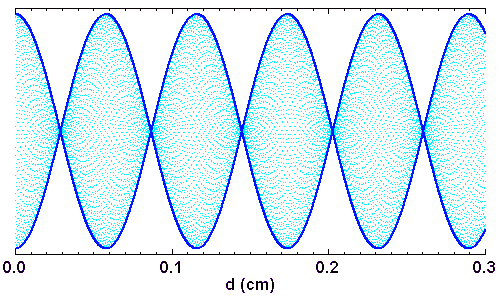
Déterminer la période des battements et représenter l'allure de l'interférogramme, pour le doublet du sodium :
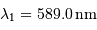 et
et 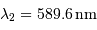 .
.
 Influence de l'inclinaison
Influence de l'inclinaison
Difficulté : ☆☆
Temps : 30 min
Les 2 miroirs d'un interféromètre de type Michelson sont réglés parallèles (au rôle de la séparatrice près).
On note 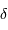 la différence de marche à incidence nulle.
la différence de marche à incidence nulle.
Question 1)
Montrer que la différence de marche pour un faisceau d'incidence  devient
devient
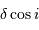 . Faire un schéma.
. Faire un schéma.
[1 points]
Question 2)
A quelle condition la différence de marche varie-t-elle de moins d'une fraction 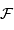 de longueur de longueur d'onde ?
de longueur de longueur d'onde ?
[1 points]
Question 3)
Faire l'application numérique pour une ddm de 1 cm, et une fraction limitée à 10%, à 1 micron.
[1 points]
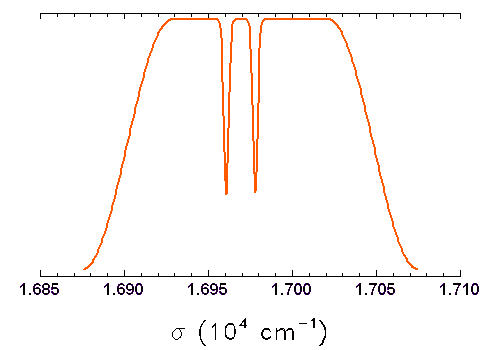
Le filtre sélectionne ici 2 raies (les raies modélisées du doublet du sodium). La variable spectrale est donnée en nombre d'onde
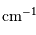
.
Crédit :
ASM
Au fil de l'interférogramme
Un interférogramme présente une modulation, de période égale à la longueur d'onde moyenne sélectionnée par le filtre.
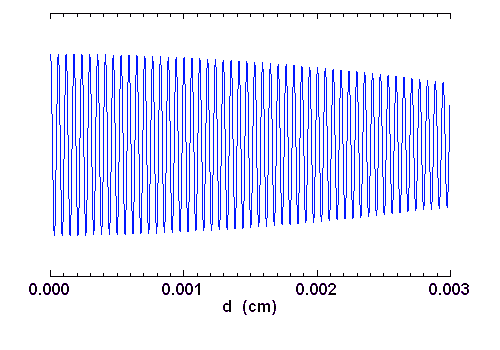
Interférogramme du
spectre synthétique du sodium. Le domaine spectral étant large, le contraste décroît avec la longueur d'onde. Les oscillations ont pour période moyenne 589.3 nm.
Crédit :
ASM
L'interférogramme présente à plus grande différence de marche des motifs liés à la nature du signal.
A très grande différence de marche, il perd tout contraste.
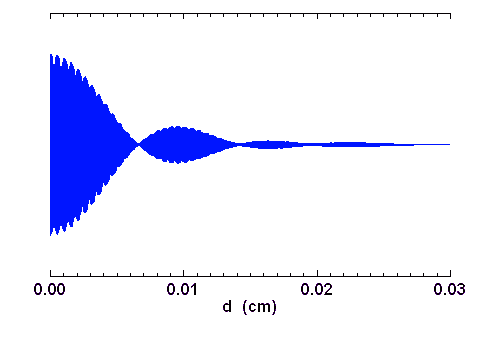
Interférogramme du
spectre
synthétique du sodium. Les motifs sont dus au doublet du
sodium. Leur effacement à grande différence de marche provient de la non-cohérence du signal spectral : les raies du sodium présentent une certaine largeur, càd une longueur de cohérence limitée. A l'échelle de cet interférogramme, la modulation présente lorsque l'on zoome sur une
portion de l'interférogramme n'est plus
visible ; on visualise ici essentiellement l'enveloppe du signal, qui représente les variations du
contraste.
Crédit :
ASM
Crédit :
ASM
 Objectifs
Objectifs
Introduire la notion de contraste, qui rend compte d'une
modulation amoindrie dans l'interférogramme d'une raie réelle, qui
n'est pas strictement monochromatique.
Le contraste représente globalement l'allure de l'interférogramme,
avec des trains de franges plus ou moins contrastés (chaque frange
n'étant localement qu'essentiellement un bout de sinusoïde de
période égale à la longueur d'onde moyenne sélectionnée par le
filtre d'entrée.
Monochromaticité
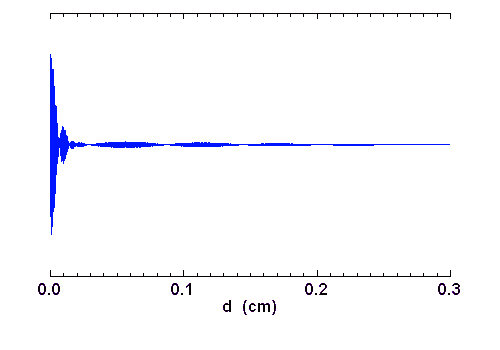
Un laser présente une bonne réalisation pratique d'une raie monochromatique. Sa longueur de cohérence peut être tellement grande que la réalisation de son interférogramme conduit effectivement à un signal également modulé à toute différence de marche :
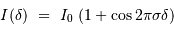
Mais une source réelle ne présente pas un telle cohérence (autrement dit, elle est moins monochromatique), et cela modifie les propriétés de l'interférogramme, qui apparaît moins contrasté.
Définition du contraste
Le contraste se mesure localement dans l'interférogramme par :
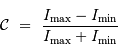
Dans l'interférogramme d'une source avec une seule raie plus ou moins large,
il intervient comme :
![I (\delta) \ = \ I_0 \ \left[ 1 + { \mathcal{C}} (\delta) \cos(2\pi\sigma\delta)\right]](../pages_fourier/equations_fts-frange/equation6.png)
Visibilité des franges d'interférence
La visibilité des franges, ou leur contraste, dépend de la largeur des raies du spectre. Une approche simple est proposée en exercice.
Des animations montrent comment la visibilité évolue avec la largeur des raies, mais aussi avec la largeur du filtre.
Visibilité
La visibilité des franges dépend de la largeur spectrale des raies étudiées. Plus les raies sont larges, moins les franges sont visibles à grande différence de marche.
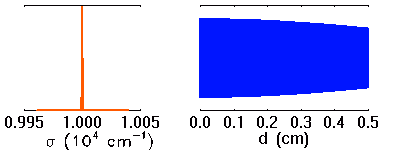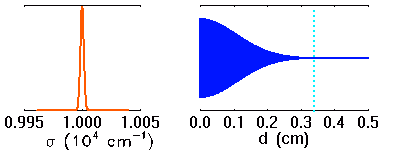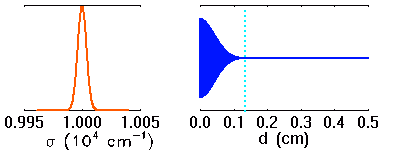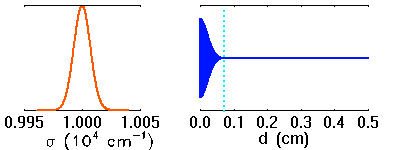
Simulation d'une raie en émission, et interférogramme associé. Lorsque la raie s'élargit, les motifs interférométriques à différence de marche élevée disparaissent.
Crédit :
ASM
 Visibilité des franges
Visibilité des franges
Difficulté : ☆☆☆
Temps : 45 min
On alimente un spectromètre par TF par un spectre avec une seule raie, non monochromatique, de largeur
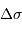 . On note
. On note 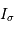 l'intensité spectrale, et
l'intensité spectrale, et 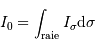 l'intensité dans la raie.
Pour simplifier les calculs, on ne s'intéresse pas à un profil réaliste,
mais à un profil de raie en émission idéalisé par :
l'intensité dans la raie.
Pour simplifier les calculs, on ne s'intéresse pas à un profil réaliste,
mais à un profil de raie en émission idéalisé par :
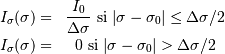
Question 1)
Justifier le fait que l'intensité totale 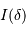 enregistrée à la différence de marche
enregistrée à la différence de marche 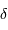 est la somme de toutes les intensités spectrales reçues.
est la somme de toutes les intensités spectrales reçues.
[3 points]
Question 2)
Mener le calcul de l'interférogramme.
[3 points]
Question 3)
Montrer la relation :
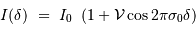
et exprimer la fonction de visibilité des franges 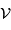 en fonction de
en fonction de
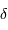 et
et 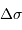 .
.
[1 points]
Question 4)
Représenter schématiquement la fonction
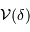 .
Déterminer la première valeur
.
Déterminer la première valeur 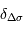 qui annule la fonction de visibilité.
qui annule la fonction de visibilité.
[2 points]
 Objectifs
Objectifs
Décortiquer le fonctionnement d'un spectromètre par transformée de
Fourier, en s'appuyant sur les propriétés d'une TF en lien avec
les caractéristiques souhaitées du spectre.
Simulations
Une observation par spectrométrie de Fourier nécessite le choix de
paramètres de Fourier efficaces pour l'enregistrement rapide de
l'interférogramme. La comparaison entre le spectre initial et le
spectre calculé à partir d'un interférogramme simulé permet de
jauger la pertinence des choix effectués.
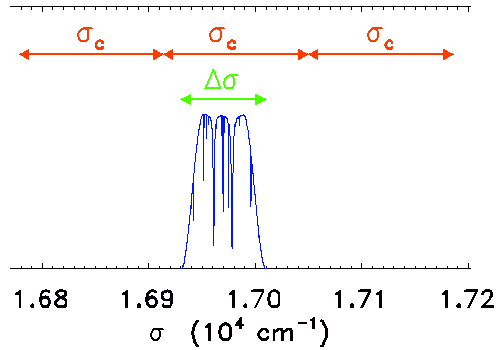
L'intervalle spectral libre contient entièrement le domaine spectral : il est suffisamment large, et les 2 bornes du signal sont comprises dans le même segment multiple de l'intervalle spectral.
Crédit :
ASM
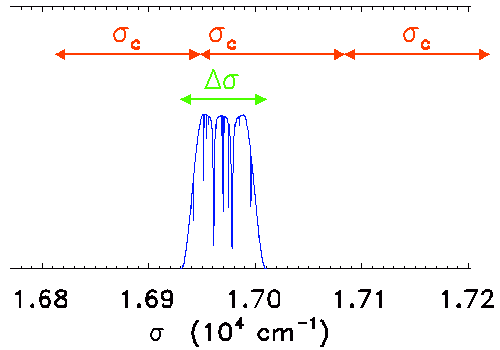
L'intervalle spectral libre ne contient pas entièrement
le domaine spectral. Le principe de la spectrométrie par TF est alors inopérant.
Crédit :
ASM
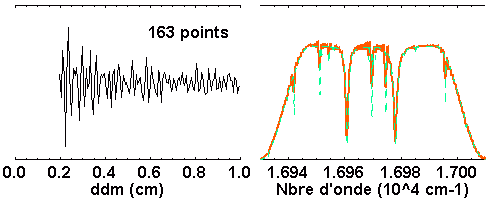
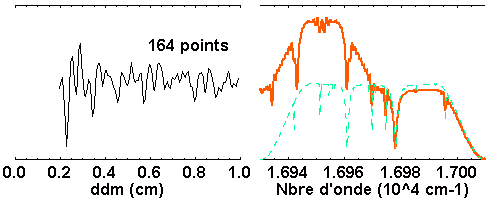
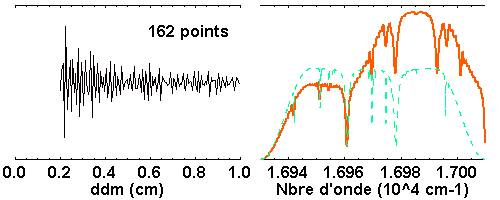
Avec 163 points, l'interférogramme est convenablement échantillonné, et
l'intervalle spectral libre inclut toutes les données. Ce n'est pas le
cas avec 162 ou 164 points : le nombre de points inadapté conduit à un mauvais repliement du spectre.
Crédit :
ASM
Intervalle spectral libre
Quand bien même la largeur de l'intervalle spectral libre est suffisante, mais avec un spectre distribué sur 2 intervalles, le résultat ne sera pas correct, par suite du repliement des fréquences lors de la fft.
Le nombre de points de l'interférogramme doit être optimisé. S'il
diffère légèrement de la valeur optimale, le mauvais échantillonnage du
signal conduit à retrouver un spectre à l'aspect tordu, par suite du
repliement indu de fréquences mal séparées.
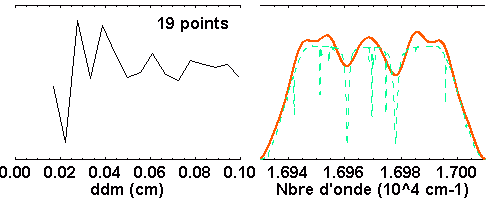

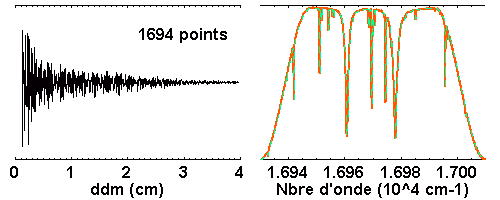
Le spectre initial est mieux reproduit lorsque l'interférogramme est obtenu avec une grande différence de marche maximale. Sur cet exemple, la résolution du spectre initial est reproduite avec un balayage de l'interférogramme jusqu'à 4 cm (R = 68000), alors que 0.1 ou 1.0 cm restent insuffisants (respectivement R = 1700 et 17000).
Crédit :
ASM

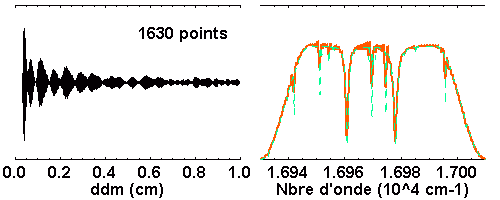
Suréchantillonner ne sert à rien. Il n'y a pas plus d'information dans
l'interférogramme à 1630 points que dans celui à 163.
Crédit :
ASM
Echantillonnage
Rien ne sert de suréchantillonner l'interférogramme dès lors que le nombre de points 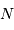 a été optimisé au sens des propriétés de la transformée de Fourier rapide.
a été optimisé au sens des propriétés de la transformée de Fourier rapide.
 Objectifs
Objectifs
Montrer comment les paramètres d'un interférogramme doivent être
choisis pour une optimisation de son acquisition respectant la
résolution spectrale désirée.
Les paramètres du spectre
Le but de l'interférométrie consiste à obtenir une information spectrale avec les éléments désirés. Les paramètre de l'interférogramme doivent donc obéir à cette contrainte.
Le spectre est essentiellement caractérisé par :
- L'intervalle spectral
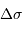 : il correspond au filtre d'entrée, à choisir en pratique parmi un lot de filtres proposés.
: il correspond au filtre d'entrée, à choisir en pratique parmi un lot de filtres proposés. - La résolution spectrale
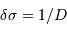 : à ajuster par l'une des propriétés de l'interférogramme.
: à ajuster par l'une des propriétés de l'interférogramme.
Critère de choix des paramètres de l'interférogramme
Le principe même de la spectrométrie par transformée de Fourier nécessite de sélectionner une région spectrale pas trop large, par un filtre adéquat, autour des raies à étudier. Ceci peut se comprendre de diverses manières : d'un point de vue expérimental, un filtre large va conduire à une teinte plate très
rapidement, de laquelle plus aucune information ne sera extractible ; du
point de vue de Fourier, il s'agit de pouvoir travailler dans une région
limitée du spectre afin qu'un échantillonnage limité, conduisant à un
intervalle spectral libre limité, suffise à recouvrer toute l'information
spectrale.
Haute résolution spectrale
Sur une source brillante, la spectrométrie par transformée de Fourier permet d'atteindre des résolutions inégalées. Ceci peut s'avérer nécessaire pour des objectifs scientifiques tels la reconnaissance d'isotopes, ou l'identification complète d'un spectre de roto-vibration
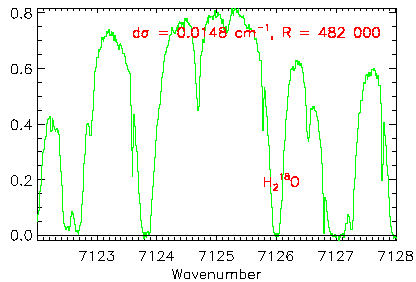
Spectre de l'eau dans l'atmosphère martienne, enregistré avec le spectromètre FTS du CFHT. L'identification de la molécule
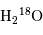
permet la mesure de l'abondance de l'isotope
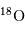
de l'oxygène.
Crédit :
CFHT
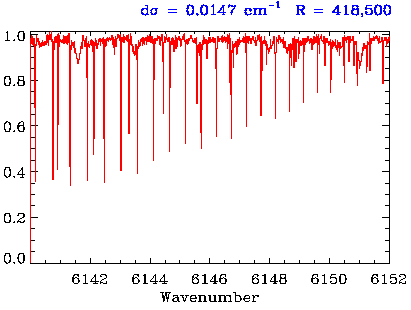
Spectre d'une bande du dioxyde de carbone de l'atmosphère martienne, enregistré avec le spectromètre FTS du CFHT.
Crédit :
CFHT
Spectro imagerie
L'étendue de faisceau admissible par un interféromètre de Fourier
permet de réaliser un spectre sur un champ étendu. L'avantage de ce principe est de pouvoir analyser toute une région spatiale dans une raie donnée, ou d'observer un point du champ à diverses longueurs d'onde, en ayant un grand choix possible de résolutions spectrales.
Ce genre d'observation a été réalisé avec le FTS du télescope CFH,
sur différents objets : les
poles de
Jupiter montrant des aurores, des
enveloppes d'hydrogène
circumstellaires, des
environnements stellaires.

Aurore polaire sur Jupiter, observée dans une raie de l'hydrogène
moléculaire.
Crédit :
CFHT
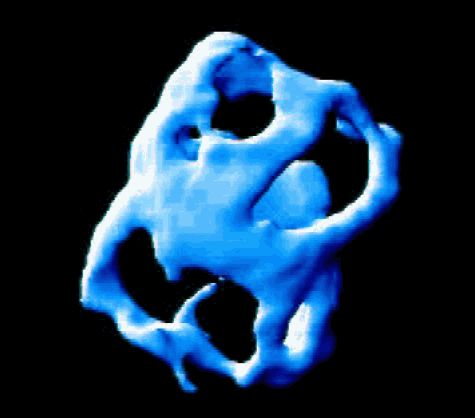
Observations de l'environnement de la nébuleuse planétaire NGC
7027, dans la raie 1-0 S(1) de l'hydrogène moléculaire. La
spectroimagerie permet ici de visualiser des régions d'isovitesse
Doppler autour de NGC 7027. Les trous sont la signature de jets à
haute vitesse.
Crédit :
CFHT
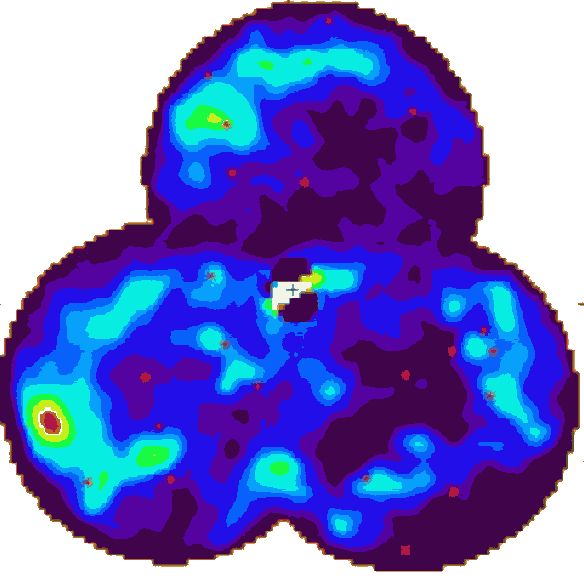
YSO (jeunes objets stellaires) dans un nuage résiduel d'hydrogène
moléculaire entourant l'étoile massive S-106 IR (plus de 15 fois
la masse du soleil).
Crédit :
CFHT

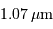 obtenu avec un FTS (Fourier Transform Spectrometer).
obtenu avec un FTS (Fourier Transform Spectrometer).


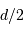 du miroir M1 par rapport à la position équilibrée conduit à une différence de marche
du miroir M1 par rapport à la position équilibrée conduit à une différence de marche 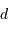 entre les 2 faisceaux recombinés par la lame séparatrice (en vert).
entre les 2 faisceaux recombinés par la lame séparatrice (en vert).
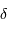 la différence de marche entre les 2 faisceaux monochromatiques interférant à l'infini, et
la différence de marche entre les 2 faisceaux monochromatiques interférant à l'infini, et 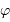 le déphasage. La relation entre
le déphasage. La relation entre 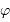 et
et 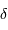 s'exprime, à la longueur d'onde
s'exprime, à la longueur d'onde 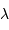 :
:
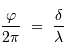
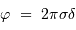
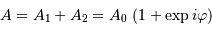
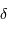 entre les 2 miroirs, sur l'axe, càd dans l'anneau central, constitue l'interférogramme.
En lumière monochromatique de nombre d'onde
entre les 2 miroirs, sur l'axe, càd dans l'anneau central, constitue l'interférogramme.
En lumière monochromatique de nombre d'onde 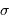 , le signal d'interférence s'écrit à la différence de marche
, le signal d'interférence s'écrit à la différence de marche 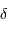 :
:
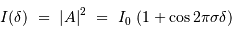
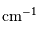 et la différence de marche, comptée en cm.
La période spatiale de l'interférogramme est
et la différence de marche, comptée en cm.
La période spatiale de l'interférogramme est 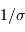 , soit tout simplement la longueur d'onde
, soit tout simplement la longueur d'onde 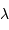 .
.
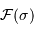 , dans la bande spectrale
, dans la bande spectrale ![[\sigma_1, \ \sigma_2]](../pages_fourier/equations_fts-instrumentation/equation19.png) ,
l'interférogramme prend la valeur :
,
l'interférogramme prend la valeur :
![I(\delta) \ = \ \int_{\sigma_1}^{\sigma_2} { \mathcal{F}}(\sigma) \ \Bigl[ 1 +\cos 2\pi \sigma \delta\Bigr] \ {\mathrm{d}} \sigma](../pages_fourier/equations_fts-instrumentation/equation20.png)
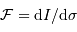 .
La partie modulée (càd qui dépend de la différence de marche
.
La partie modulée (càd qui dépend de la différence de marche 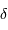 ) de l'interférogramme, correspond à la partie réelle de la TF de la densité spectrale :
) de l'interférogramme, correspond à la partie réelle de la TF de la densité spectrale :
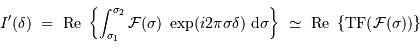
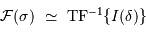


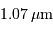 obtenu avec le FTS (Fourier Transform Spectrometer) du télescope CFH.
obtenu avec le FTS (Fourier Transform Spectrometer) du télescope CFH.



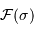 .
.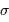 , exprimé en
, exprimé en
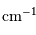 .
.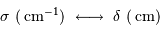
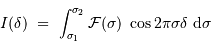
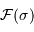 .
.

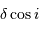 , avec
, avec  l'inclinaison, autour de l'inclinaison nulle, la tache centrale est relativement plus large que les autres anneaux.
l'inclinaison, autour de l'inclinaison nulle, la tache centrale est relativement plus large que les autres anneaux.

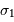 et
et 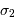 voisins. Chacune des raies est supposée monochromatique, et leurs intensités égales.
voisins. Chacune des raies est supposée monochromatique, et leurs intensités égales.
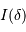 . Mettre en
évidence deux périodes caractéristiques de l'interférogramme.
. Mettre en
évidence deux périodes caractéristiques de l'interférogramme.
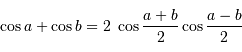
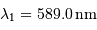 et
et 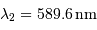 .
.
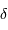 la différence de marche à incidence nulle.
la différence de marche à incidence nulle.
 devient
devient
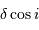 . Faire un schéma.
. Faire un schéma.
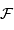 de longueur de longueur d'onde ?
de longueur de longueur d'onde ?

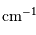 .
.



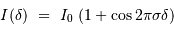
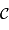 des franges est le rapport entre l'amplitude de modulation de la frange à l'énergie totale
des franges est le rapport entre l'amplitude de modulation de la frange à l'énergie totale 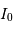 collectée dans le filtre.
collectée dans le filtre.
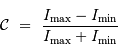
![I (\delta) \ = \ I_0 \ \left[ 1 + { \mathcal{C}} (\delta) \cos(2\pi\sigma\delta)\right]](../pages_fourier/equations_fts-frange/equation6.png)

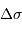 . On note
. On note 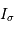 l'intensité spectrale, et
l'intensité spectrale, et 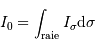 l'intensité dans la raie.
Pour simplifier les calculs, on ne s'intéresse pas à un profil réaliste,
mais à un profil de raie en émission idéalisé par :
l'intensité dans la raie.
Pour simplifier les calculs, on ne s'intéresse pas à un profil réaliste,
mais à un profil de raie en émission idéalisé par :
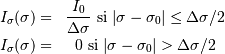
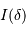 enregistrée à la différence de marche
enregistrée à la différence de marche 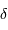 est la somme de toutes les intensités spectrales reçues.
est la somme de toutes les intensités spectrales reçues.
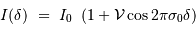
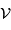 en fonction de
en fonction de
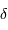 et
et 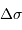 .
.
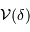 .
Déterminer la première valeur
.
Déterminer la première valeur 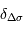 qui annule la fonction de visibilité.
qui annule la fonction de visibilité.
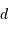 , admet une fréquence de coupure
, admet une fréquence de coupure 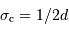 . La valeur de cette fréquence, donc la valeur de
. La valeur de cette fréquence, donc la valeur de 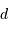 , ne peuvent pas être prises au hasard.
, ne peuvent pas être prises au hasard.
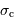 , encadrent entièrement
, encadrent entièrement 






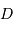 explorée. Elle s'exprime simplement :
explorée. Elle s'exprime simplement :
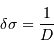
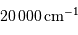 et
et 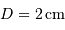 ,
, 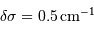 et le pouvoir de résolution vaut donc
et le pouvoir de résolution vaut donc 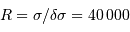 .
.

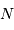 a été optimisé au sens des propriétés de la transformée de Fourier rapide.
a été optimisé au sens des propriétés de la transformée de Fourier rapide.
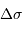 : il correspond au filtre d'entrée, à choisir en pratique parmi un lot de filtres proposés.
: il correspond au filtre d'entrée, à choisir en pratique parmi un lot de filtres proposés.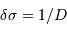 : à ajuster par l'une des propriétés de l'interférogramme.
: à ajuster par l'une des propriétés de l'interférogramme.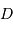
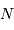 entre la différence de marche nulle
et la différence de marche maximale
entre la différence de marche nulle
et la différence de marche maximale 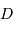 , équidistants de
, équidistants de 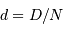 .
.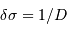
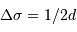
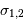 respectivement les bornes inférieure et supérieure de la bande passante utile.
La largeur de la bande passante
respectivement les bornes inférieure et supérieure de la bande passante utile.
La largeur de la bande passante 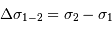 détermine le domaine des nombres d'onde dans lequel il ne doit pas y
avoir confusion spectrale.
détermine le domaine des nombres d'onde dans lequel il ne doit pas y
avoir confusion spectrale.
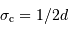 telle que la largeur spectrale
telle que la largeur spectrale ![[\sigma_1, \ \sigma_2]](../pages_fourier/equations_fts-enregistrement/equation12.png) du filtre soit comprise dans l'intervalle spectral libre
du filtre soit comprise dans l'intervalle spectral libre ![[n \sigma _{\mathrm{c}}, \ (n+1) \sigma _{\mathrm{c}}]](../pages_fourier/equations_fts-enregistrement/equation13.png) :
:
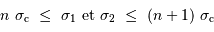
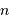 un entier naturel.
un entier naturel.
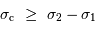 .
Si l'on suppose la différence de marche maximale
.
Si l'on suppose la différence de marche maximale 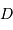 fixée, et donc la
résolution fixée, on peut
préciser le choix du nombre de points optimal
fixée, et donc la
résolution fixée, on peut
préciser le choix du nombre de points optimal 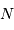 , résultant des 2
conditions ci-dessus.
, résultant des 2
conditions ci-dessus.
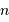 et
et 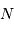 doivent être entiers, leurs solutions réelles doivent vérifier :
doivent être entiers, leurs solutions réelles doivent vérifier :
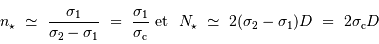
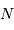 et
et 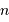 assurant de façon optimale :
assurant de façon optimale :
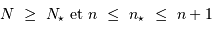
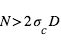 et simultanément
et simultanément
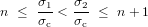
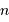 et
et 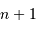 assurent la validité de l'intervalle spectral
assurent la validité de l'intervalle spectral 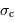 défini par
défini par 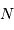 .
.
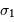
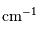
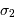
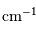
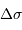
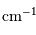
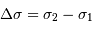
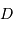
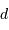
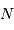
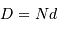
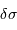
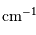
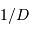
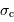
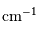
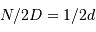
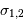 = bornes min et max du filtre)
= bornes min et max du filtre) = ddm
maximale)
= ddm
maximale)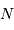 = nbre de points dans l'interférogramme)
= nbre de points dans l'interférogramme)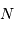 adaptée à l'intervalle spectral
adaptée à l'intervalle spectral
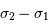 et à la résolution proposée.
et à la résolution proposée.
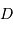 .
.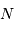 voisin mais différent de la
valeur proposée.
voisin mais différent de la
valeur proposée.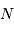 très grand.
très grand.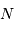 élevées.
élevées.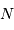 élevées.
élevées.
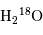 permet la mesure de l'abondance de l'isotope
permet la mesure de l'abondance de l'isotope 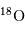 de l'oxygène.
de l'oxygène.




![I(\delta) \ = \ I_0 \ \left[1 + \cos(2\pi \sigma_1 \delta)\right] + I_0 \ \left[1 + \cos(2\pi \sigma_2 \delta)\right]](../pages_fourier/equations_fts-interferogramme/equation14.png)
![I(\delta) \ = \ 2\ I_0 \ \left[1 +\cos\bigl(\pi (\sigma_1+\sigma_2) \delta\bigr) \cos\bigl(\pi (\sigma_1-\sigma_2) \delta\bigr)\right]](../pages_fourier/equations_fts-interferogramme/equation15.png)
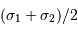 , modulé par une enveloppe de fréquence
, modulé par une enveloppe de fréquence 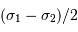 .
.
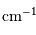 , soit une demi-différence de
, soit une demi-différence de 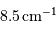 .
.
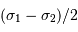 , la période spatiale est donc :
, la période spatiale est donc :
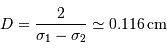
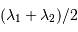 .
.