Le biais de Malmquist
Les observations extragalactiques portent sur des objets certes intrinsèquement très lumineux, mais apparemment très peu lumineux, et souvent si peu lumineux que la non détection des moins lumineux d'entre eux peut provoquer un biais dans les résultats observationnels. Ce biais peut affecter toute mesure statistique supposant, à tort, une population homogène d'objets.
Biais de Malmquist
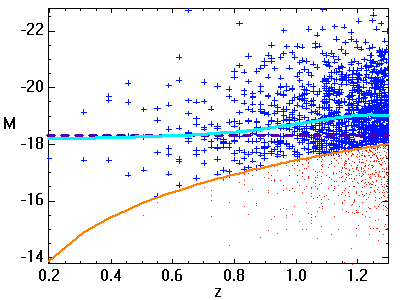
Identification du biais de Malmquist. Le graphe présente la magnitude absolue de galaxies très distantes, fonction de leur distance cosmologique
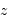
. Le nombre d'objets observés croît comme le carré de la distance. A grande distance, la non-détection des moins lumineux (objets indiqués en rouge) biaise la distribution observée. La moyenne des magnitudes absolues (en bleu) s'en ressent : elle est inférieure à ce que l'on observerait sans biais.
Crédit :
ASM
 Objectifs
Objectifs
Les premiers travaux utilisant la relation Tully-Fisher conduisirent dans les années 1980 à une valeur élevée de la constante de Hubble - de l'ordre de 100 km/s/Mpc - ainsi qu'à une croissance de 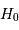 avec la distance. Ces résultats proviennent de la nature statistique de la relation
Tully-Fisher et du fait que les échantillons sont toujours limités en magnitude apparente.
avec la distance. Ces résultats proviennent de la nature statistique de la relation
Tully-Fisher et du fait que les échantillons sont toujours limités en magnitude apparente.
Propriété statistique
A toutes les galaxies ayant la même vitesse de rotation 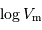 (ou appartenant à une classe de sosies), on attribue la même magnitude absolue (ou luminosité) selon la relation linéaire :
(ou appartenant à une classe de sosies), on attribue la même magnitude absolue (ou luminosité) selon la relation linéaire :
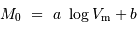
Chaque détermination individuelle souffre en fait d'une imprécision due à l'écart entre la magnitude
absolue exacte et la valeur moyenne  adoptée. Si on considère maintenant un grand nombre
d'objets, on détermine donc un ensemble de distances dont chacune est affectée d'une erreur, les unes étant surestimées, les autres sous-estimées. On espère cependant qu'elles soient exactes en moyenne.
adoptée. Si on considère maintenant un grand nombre
d'objets, on détermine donc un ensemble de distances dont chacune est affectée d'une erreur, les unes étant surestimées, les autres sous-estimées. On espère cependant qu'elles soient exactes en moyenne.
Biais de Malmquist
K.G. Malmquist (1920) a montré que ce n'est pas le cas si l'échantillon utilisé est limité en magnitude apparente : l'échantillon contient alors en effet une plus grande proportion de galaxies intrinsèquement plus lumineuses que  ,
et une moins grande proportion de galaxies moins lumineuses. La magnitude absolue moyenne de l'ensemble des galaxies du catalogue n'est donc pas égale, mais inférieure à
,
et une moins grande proportion de galaxies moins lumineuses. La magnitude absolue moyenne de l'ensemble des galaxies du catalogue n'est donc pas égale, mais inférieure à  .
.
Il s'ensuit qu'en sous-estimant ainsi la luminosité moyenne des galaxies observées, on sous-estime leurs distances, et l'on surestime la constante de Hubble.
Le biais de Malmquist
L'animation ci-jointe montre comment le biais de Malmquist dépend de la magnitude limite d'observation. Plus elle est élevée, moins le biais est important.
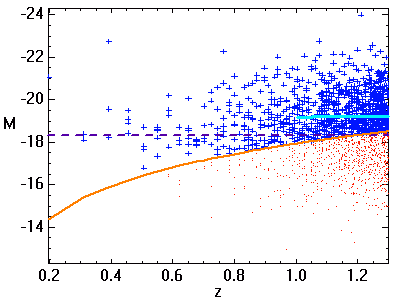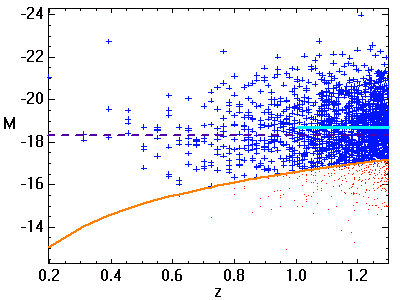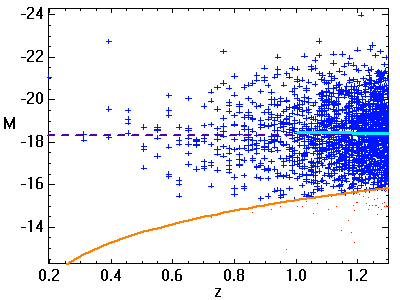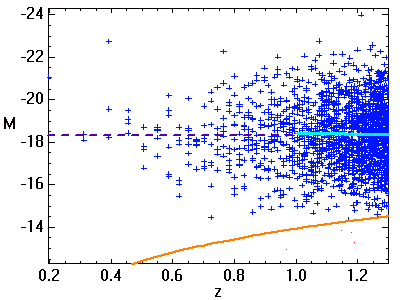
Plus la magnitude limite d'observation augmente (courbe orange), mieux la distribution des cibles les moins lumineuses est perçue. Il s'ensuit une meilleure détermination de la magnitude absolue moyenne (courbe bleu ciel).
Crédit :
ASM
 Les galaxies sosies
Les galaxies sosies
Difficulté : ☆☆☆
Temps : 1 h
On se propose d'estimer la constante de Hubble et l'âge de l'univers en utilisant les sosies d'une galaxie bien connue : la galaxie d'Andromède (M31). Le tableau donne les paramètres d'une trentaine de galaxies sélectionnées dans la base de données extragalactiques LEDA selon les critères de morphologie (spirale), d'inclinaison ou de rapport d'axe 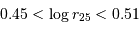 (
(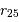 est le rapport du grand au petit axe, repéré à l'isophote de magnitude 25), vitesse de rotation (en km/s) dont le logarithme vérifie
est le rapport du grand au petit axe, repéré à l'isophote de magnitude 25), vitesse de rotation (en km/s) dont le logarithme vérifie 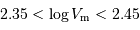 , et avec un seuil en magnitude
, et avec un seuil en magnitude 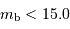 .
.
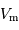 est le maximum de la vitesse de rotation dans le disque, et
est le maximum de la vitesse de rotation dans le disque, et 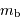 est la magnitude apparente dans la bande
est la magnitude apparente dans la bande 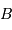 .
.
La magnitude apparente de M31 (PGC 2557) vaut 3.20 ; sa distance, déterminée au moyen de céphéides observées par le télescope spatial Hubble, est estimée à 0.841 Mpc, ce qui représente un module de distance de 24.6 (avec la distance exprimée en Mpc, 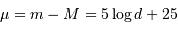 ).
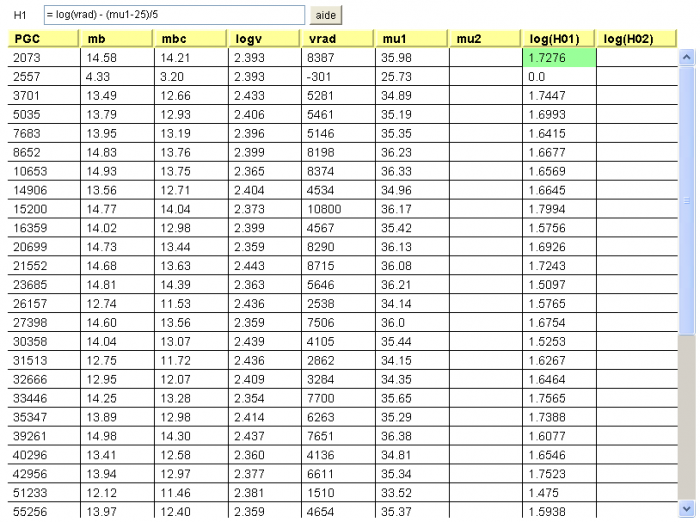
Le tableau fournit, pour chaque galaxie repérée par son numéro PGC : la magnitude apparente mb, une valeur corrigée
).
Le tableau fournit, pour chaque galaxie repérée par son numéro PGC : la magnitude apparente mb, une valeur corrigée 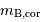 , le logarithme de la vitesse maximale de rotation de la galaxie (logv), et sa vitesse radiale héliocentrique (vrad).
, le logarithme de la vitesse maximale de rotation de la galaxie (logv), et sa vitesse radiale héliocentrique (vrad).

Question 1)
Déterminer la magnitude absolue de M31. Quelle hypothèse fait-on sur les magnitudes absolues de ses sosies ?
La magnitude apparente de M31 et son module de distance sont donnés.
Question 2)
Déterminer pour chaque galaxie son module de distance et en déduire la valeur de la constante de Hubble associée :
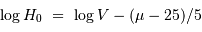
A l'aide de l'appliquette, calculer le module de distance mu1.
Toujours à l'aide de l'appliquette, déduire 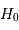 (log(H01)) du module de distance mu1.
(log(H01)) du module de distance mu1.
Question 3)
Déterminer le module de distance mu2 par application de la relation de Tully-Fisher, avec les coefficients 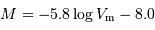 .
En déduire une autre estimation de
.
En déduire une autre estimation de 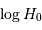 .
.
Question 4)
Calculer dans chaque cas la moyenne des valeurs 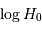 et en déduire une valeur de la constante de Hubble. Commenter.
et en déduire une valeur de la constante de Hubble. Commenter.
Estimer la moyenne en représentant 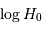 en fonction de PGC.
en fonction de PGC.
Question 5)
Représenter les valeurs 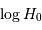 en fonction de la vitesse radiale pour les galaxies sosies de M31. Commenter.
en fonction de la vitesse radiale pour les galaxies sosies de M31. Commenter.
Question 6)
Appliquer la correction de Malmquist et calculer la valeur corrigée de 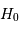 . Comparer aux valeurs obtenues précédemment, par le module de distance ou par la relation Tully-Fisher.
. Comparer aux valeurs obtenues précédemment, par le module de distance ou par la relation Tully-Fisher.
Question 7)
Dans le modèle standard 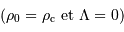 , l'âge de l'univers est égal à 2/3 du temps de Hubble
, l'âge de l'univers est égal à 2/3 du temps de Hubble 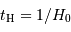 . Calculer cet âge à partir des valeurs de
. Calculer cet âge à partir des valeurs de 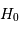 obtenues précédemment. On rappelle que la constante est exprimée en km/s/Mpc.
obtenues précédemment. On rappelle que la constante est exprimée en km/s/Mpc.
Convertir les unités km/s/Mpc en l'inverse d'un temps.
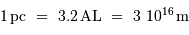 .
.
- Question 1
Aide :
La magnitude apparente de M31 et son module de distance sont donnés.
Aide :
M31 = PGC 2557
Solution :
Par application de la relation donnant le module de distance :
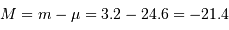
Toutes les galaxie sosies de M31 sont supposées avoir la même magnitude absolue.
- Question 2
Aide :
A l'aide de l'appliquette, calculer le module de distance mu1.
Aide :
Toujours à l'aide de l'appliquette, déduire  (log(H01)) du module de distance mu1.
(log(H01)) du module de distance mu1.
Solution :
Le calcul, via l'appliquette, du module de distance est immédiat.
 , avec
, avec 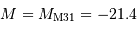 (sélectionner la case F1 et taper la commande = B1 + 21.4 ou bien
= mb + 21.4).
(sélectionner la case F1 et taper la commande = B1 + 21.4 ou bien
= mb + 21.4).
Ensuite, on déduit 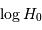 par la relation demandée
(sélectionner la case H1 et taper la commande = log(E1) - (F1-25)/5. ou bien = log(vrad) - (mu1-25)/5). Attention à sélectionner la bonne vitesse (vrad : vitesse radiale héliocentrique).
par la relation demandée
(sélectionner la case H1 et taper la commande = log(E1) - (F1-25)/5. ou bien = log(vrad) - (mu1-25)/5). Attention à sélectionner la bonne vitesse (vrad : vitesse radiale héliocentrique).
Crédit :
ASM
- Question 3
Solution :
En appliquant la relation de Tully-Fisher pour le module de distance,
on calcule 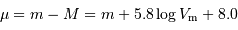 (via la sélection de G1 et =mb+5.8*logv+8).
(via la sélection de G1 et =mb+5.8*logv+8).
Ensuite, on déduit 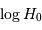 par la relation demandée
(sélectionner la case I1 et taper la commande =log(E1)-(G1-25)/5. ou bien =log(vrad) -(mu2-25)/5).
par la relation demandée
(sélectionner la case I1 et taper la commande =log(E1)-(G1-25)/5. ou bien =log(vrad) -(mu2-25)/5).
Crédit :
ASM
- Question 4
Aide :
Estimer la moyenne en représentant 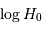 en fonction de PGC.
en fonction de PGC.
Solution :
Pour la valeur log(H01), on estime la moyenne à 1.65, pour log(H02), elle vaut plutôt 1.55.
- Question 5
Solution :
On s'aperçoit que  augmente avec la vitesse radiale, et donc avec la distance. Ceci est incompatible avec la relation linéaire énoncée par la loi de Hubble. Mais l'effet n'est pas réel ; il provient du biais induit par la coupure en magnitude à grande distance.
augmente avec la vitesse radiale, et donc avec la distance. Ceci est incompatible avec la relation linéaire énoncée par la loi de Hubble. Mais l'effet n'est pas réel ; il provient du biais induit par la coupure en magnitude à grande distance.
- Question 6
Aide :
Voir le cours.
Solution :
La correction de Malmquist revient à corriger  à la baisse de 23%. On obtient donc, de
à la baisse de 23%. On obtient donc, de 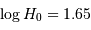 , la valeur non corrigée d'environ 44 km/s/Mpc, qui devient après correction environ 33 km/s/Mpc.
, la valeur non corrigée d'environ 44 km/s/Mpc, qui devient après correction environ 33 km/s/Mpc.
- Question 7
Aide :
Convertir les unités km/s/Mpc en l'inverse d'un temps.
Aide :
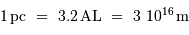 .
.
Solution :
La définition du temps de Hubble est :
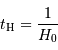
L'unité à traiter est le Mpc/km s. Comme
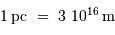 ,
,
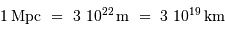 .
Par ailleurs,
.
Par ailleurs, 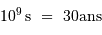 .
.
On en déduit le temps de Hubble, de l'ordre de 27 milliards d'années, d'où l'âge de l'Univers de l'ordre de 18 milliards d'années dans le cadre de ce modèle.

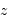 . Le nombre d'objets observés croît comme le carré de la distance. A grande distance, la non-détection des moins lumineux (objets indiqués en rouge) biaise la distribution observée. La moyenne des magnitudes absolues (en bleu) s'en ressent : elle est inférieure à ce que l'on observerait sans biais.
. Le nombre d'objets observés croît comme le carré de la distance. A grande distance, la non-détection des moins lumineux (objets indiqués en rouge) biaise la distribution observée. La moyenne des magnitudes absolues (en bleu) s'en ressent : elle est inférieure à ce que l'on observerait sans biais.
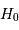 avec la distance. Ces résultats proviennent de la nature statistique de la relation
Tully-Fisher et du fait que les échantillons sont toujours limités en magnitude apparente.
avec la distance. Ces résultats proviennent de la nature statistique de la relation
Tully-Fisher et du fait que les échantillons sont toujours limités en magnitude apparente.
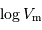 (ou appartenant à une classe de sosies), on attribue la même magnitude absolue (ou luminosité) selon la relation linéaire :
(ou appartenant à une classe de sosies), on attribue la même magnitude absolue (ou luminosité) selon la relation linéaire :
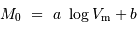
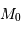 adoptée. Si on considère maintenant un grand nombre
d'objets, on détermine donc un ensemble de distances dont chacune est affectée d'une erreur, les unes étant surestimées, les autres sous-estimées. On espère cependant qu'elles soient exactes en moyenne.
adoptée. Si on considère maintenant un grand nombre
d'objets, on détermine donc un ensemble de distances dont chacune est affectée d'une erreur, les unes étant surestimées, les autres sous-estimées. On espère cependant qu'elles soient exactes en moyenne.
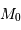 ,
et une moins grande proportion de galaxies moins lumineuses. La magnitude absolue moyenne de l'ensemble des galaxies du catalogue n'est donc pas égale, mais inférieure à
,
et une moins grande proportion de galaxies moins lumineuses. La magnitude absolue moyenne de l'ensemble des galaxies du catalogue n'est donc pas égale, mais inférieure à 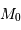 .
.
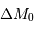 et donc sur le module de distance des galaxies peut s'exprimer de manière simple en fonction de la dispersion
et donc sur le module de distance des galaxies peut s'exprimer de manière simple en fonction de la dispersion 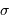 du critère de distance (l'incertitude moyenne par rapport à
du critère de distance (l'incertitude moyenne par rapport à 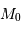 ) :
) :

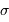 de l'ordre de 0.6 magnitude, typiquement ce que l'on obtient par la
de l'ordre de 0.6 magnitude, typiquement ce que l'on obtient par la
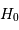 surestimée d'autant.
surestimée d'autant.

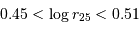 (
(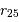 est le rapport du grand au petit axe, repéré à l'isophote de magnitude 25), vitesse de rotation (en km/s) dont le logarithme vérifie
est le rapport du grand au petit axe, repéré à l'isophote de magnitude 25), vitesse de rotation (en km/s) dont le logarithme vérifie 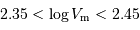 , et avec un seuil en magnitude
, et avec un seuil en magnitude 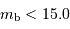 .
.
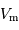 est le maximum de la vitesse de rotation dans le disque, et
est le maximum de la vitesse de rotation dans le disque, et 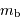 est la magnitude apparente dans la bande
est la magnitude apparente dans la bande 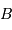 .
.
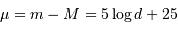 ).
Le tableau fournit, pour chaque galaxie repérée par son numéro PGC : la magnitude apparente
).
Le tableau fournit, pour chaque galaxie repérée par son numéro PGC : la magnitude apparente 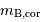 , le logarithme de la vitesse maximale de rotation de la galaxie (
, le logarithme de la vitesse maximale de rotation de la galaxie (
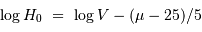
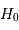 (
(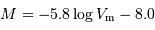 .
En déduire une autre estimation de
.
En déduire une autre estimation de 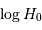 .
.
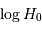 et en déduire une valeur de la constante de Hubble. Commenter.
et en déduire une valeur de la constante de Hubble. Commenter.
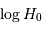 en fonction de PGC.
en fonction de PGC.
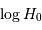 en fonction de la vitesse radiale pour les galaxies sosies de M31. Commenter.
en fonction de la vitesse radiale pour les galaxies sosies de M31. Commenter.
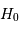 . Comparer aux valeurs obtenues précédemment, par le module de distance ou par la relation Tully-Fisher.
. Comparer aux valeurs obtenues précédemment, par le module de distance ou par la relation Tully-Fisher.
 , l'âge de l'univers est égal à 2/3 du temps de Hubble
, l'âge de l'univers est égal à 2/3 du temps de Hubble 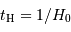 . Calculer cet âge à partir des valeurs de
. Calculer cet âge à partir des valeurs de 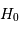 obtenues précédemment. On rappelle que la constante est exprimée en km/s/Mpc.
obtenues précédemment. On rappelle que la constante est exprimée en km/s/Mpc.
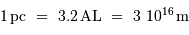 .
.
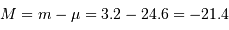
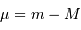 , avec
, avec 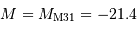 (sélectionner la case F1 et taper la commande
(sélectionner la case F1 et taper la commande 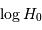 par la relation demandée
(sélectionner la case H1 et taper la commande
par la relation demandée
(sélectionner la case H1 et taper la commande 
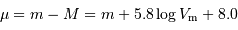 (via la sélection de G1 et
(via la sélection de G1 et 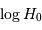 par la relation demandée
(sélectionner la case I1 et taper la commande
par la relation demandée
(sélectionner la case I1 et taper la commande 
 augmente avec la vitesse radiale, et donc avec la distance. Ceci est incompatible avec la relation linéaire énoncée par la loi de Hubble. Mais l'effet n'est pas réel ; il provient du biais induit par la coupure en magnitude à grande distance.
augmente avec la vitesse radiale, et donc avec la distance. Ceci est incompatible avec la relation linéaire énoncée par la loi de Hubble. Mais l'effet n'est pas réel ; il provient du biais induit par la coupure en magnitude à grande distance.
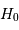 à la baisse de 23%. On obtient donc, de
à la baisse de 23%. On obtient donc, de 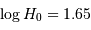 , la valeur non corrigée d'environ 44 km/s/Mpc, qui devient après correction environ 33 km/s/Mpc.
, la valeur non corrigée d'environ 44 km/s/Mpc, qui devient après correction environ 33 km/s/Mpc.
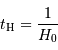
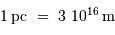 ,
,
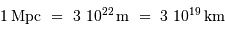 .
Par ailleurs,
.
Par ailleurs, 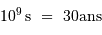 .
.