
|
Les premiers travaux utilisant la relation Tully-Fisher conduisirent dans les années 1980 à une valeur élevée de la constante de Hubble - de l'ordre de 100 km/s/Mpc - ainsi qu'à une croissance de 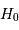 avec la distance. Ces résultats proviennent de la nature statistique de la relation
Tully-Fisher et du fait que les échantillons sont toujours limités en magnitude apparente.
avec la distance. Ces résultats proviennent de la nature statistique de la relation
Tully-Fisher et du fait que les échantillons sont toujours limités en magnitude apparente.
A toutes les galaxies ayant la même vitesse de rotation 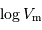 (ou appartenant à une classe de sosies), on attribue la même magnitude absolue (ou luminosité) selon la relation linéaire :
(ou appartenant à une classe de sosies), on attribue la même magnitude absolue (ou luminosité) selon la relation linéaire :
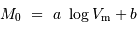
Chaque détermination individuelle souffre en fait d'une imprécision due à l'écart entre la magnitude
absolue exacte et la valeur moyenne 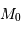 adoptée. Si on considère maintenant un grand nombre
d'objets, on détermine donc un ensemble de distances dont chacune est affectée d'une erreur, les unes étant surestimées, les autres sous-estimées. On espère cependant qu'elles soient exactes en moyenne.
adoptée. Si on considère maintenant un grand nombre
d'objets, on détermine donc un ensemble de distances dont chacune est affectée d'une erreur, les unes étant surestimées, les autres sous-estimées. On espère cependant qu'elles soient exactes en moyenne.
K.G. Malmquist (1920) a montré que ce n'est pas le cas si l'échantillon utilisé est limité en magnitude apparente : l'échantillon contient alors en effet une plus grande proportion de galaxies intrinsèquement plus lumineuses que 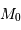 ,
et une moins grande proportion de galaxies moins lumineuses. La magnitude absolue moyenne de l'ensemble des galaxies du catalogue n'est donc pas égale, mais inférieure à
,
et une moins grande proportion de galaxies moins lumineuses. La magnitude absolue moyenne de l'ensemble des galaxies du catalogue n'est donc pas égale, mais inférieure à 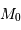 .
.
Il s'ensuit qu'en sous-estimant ainsi la luminosité moyenne des galaxies observées, on sous-estime leurs distances, et l'on surestime la constante de Hubble.
Si on suppose que les galaxies sont réparties uniformément dans l'espace, l'erreur statistique sur la magnitude absolue 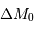 et donc sur le module de distance des galaxies peut s'exprimer de manière simple en fonction de la dispersion
et donc sur le module de distance des galaxies peut s'exprimer de manière simple en fonction de la dispersion 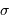 du critère de distance (l'incertitude moyenne par rapport à
du critère de distance (l'incertitude moyenne par rapport à 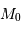 ) :
) :

Pour une dispersion 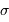 de l'ordre de 0.6 magnitude, typiquement ce que l'on obtient par la
relation Tully-Fisher
ou la méthode des sosies, cela donne sur le module de distance une erreur de - 0.5 magnitude. On obtient finalement sur la distance une sous-estimation de l'ordre de 23%, et une valeur de
de l'ordre de 0.6 magnitude, typiquement ce que l'on obtient par la
relation Tully-Fisher
ou la méthode des sosies, cela donne sur le module de distance une erreur de - 0.5 magnitude. On obtient finalement sur la distance une sous-estimation de l'ordre de 23%, et une valeur de 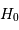 surestimée d'autant.
surestimée d'autant.