S'exercer

Les galaxies sosies

Difficulté : ☆☆☆ Temps : 1 h

On se propose d'estimer la constante de Hubble et l'âge de l'univers en utilisant les sosies d'une galaxie bien connue : la galaxie d'Andromède (M31). Le tableau donne les paramètres d'une trentaine de galaxies sélectionnées dans la base de données extragalactiques LEDA selon les critères de morphologie (spirale), d'inclinaison ou de rapport d'axe 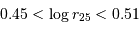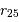$0.45 < \log r_{25} < 0.51$ ( $r_{25}$ est le rapport du grand au petit axe, repéré à l'isophote de magnitude 25), vitesse de rotation (en km/s) dont le logarithme vérifie 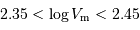$2.35 < \log V _{\mathrm{m}} < 2.45$ , et avec un seuil en magnitude 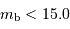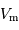$m _{\mathrm{b}} < 15.0$ . $V _{\mathrm{m}}$ est le maximum de la vitesse de rotation dans le disque, et 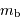$m _{\mathrm{b}}$ est la magnitude apparente dans la bande .

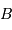La magnitude apparente de M31 (PGC 2557) vaut 3.20 ; sa distance, déterminée au moyen de céphéides observées par le télescope spatial Hubble, est estimée à 0.841 Mpc, ce qui représente un module de distance de 24.6 (avec la distance exprimée en Mpc, 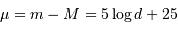$\mu = m - M = 5 \log d + 25$ ). 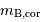Le tableau fournit, pour chaque galaxie repérée par son numéro PGC : la magnitude apparente mb, une valeur corrigée $m _{\mathrm{B, cor}}$ , le logarithme de la vitesse maximale de rotation de la galaxie (logv), et sa vitesse radiale héliocentrique (vrad).

Question 1)

Déterminer la magnitude absolue de M31. Quelle hypothèse fait-on sur les magnitudes absolues de ses sosies ?

Aide Aide Solution

Question 2)

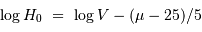
Déterminer pour chaque galaxie son module de distance et en déduire la valeur de la constante de Hubble associée : $\log H_0\ =\ \log V - (\mu -25)/5$

Aide Aide Solution

Question 3)

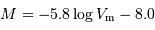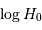Déterminer le module de distance mu2 par application de la relation de Tully-Fisher, avec les coefficients $M = -5.8 \log V _{\mathrm{m}} - 8.0$ . En déduire une autre estimation de $\log H_0$ .

Solution

Question 4)

Calculer dans chaque cas la moyenne des valeurs 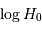$\log H_0$ et en déduire une valeur de la constante de Hubble. Commenter.

Aide Solution

Question 5)

Représenter les valeurs 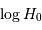$\log H_0$ en fonction de la vitesse radiale pour les galaxies sosies de M31. Commenter.

Solution

Question 6)

Appliquer la correction de Malmquist et calculer la valeur corrigée de 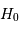H_0 . Comparer aux valeurs obtenues précédemment, par le module de distance ou par la relation Tully-Fisher.

Aide Solution

Question 7)

Dans le modèle standard $(\rho_0 = \rho _{\mathrm{c}} \mathrm{\ et\ } \Lambda = 0)$ , l'âge de l'univers est égal à 2/3 du temps de Hubble $t _{\mathrm{H}} = 1/ H_0$ . Calculer cet âge à partir des valeurs de H_0 obtenues précédemment. On rappelle que la constante est exprimée en km/s/Mpc.

Aide Aide Solution