
|
Dans un modèle d'univers non-statique à espace temps variable, la loi de Hubble existe, même si toutes les galaxies sont comobiles avec le système de coordonnées, i.e. si leur énergie cinétique est nulle, aux mouvements propres près. La métrique non-statique la plus générale est la métrique de Robertson-Walker qui s'écrit:
![{\mathrm{d}} s^2 = - R(t)^2 \left[ \frac{ {\mathrm{d}} r^2}{1-kr^2} + r^2 ( {\mathrm{d}}\theta^2 + \sin^2\theta {\mathrm{d}}\phi^2) \right] + c^2 {\mathrm{d}} t^2](../pages_indicateur-secondaire/equations_cosmologie/equation1.png)
où 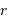 ,
, 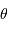 ,
, 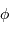 sont les paramètres d'espace et
sont les paramètres d'espace et 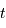 le temps. La fonction
le temps. La fonction 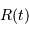 représente le rayon de l'univers à l'instant
représente le rayon de l'univers à l'instant 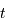 .
.
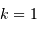 , l'univers est à géométrie sphérique, et
l'espace est fini.
, l'univers est à géométrie sphérique, et
l'espace est fini.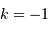 , l'univers est à géométrie hyperbolique, et
l'espace est à chaque instant ouvert et infini.
, l'univers est à géométrie hyperbolique, et
l'espace est à chaque instant ouvert et infini.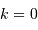 , l'univers est à géométrie parabolique, et
l'espace est aussi ouvert et infini, mais il est à chaque instant
isométrique à un espace plat euclidien.
, l'univers est à géométrie parabolique, et
l'espace est aussi ouvert et infini, mais il est à chaque instant
isométrique à un espace plat euclidien.
C'est la densité massique de l'univers qui détermine son type de géométrie. Une forte densité courbe l'espace au point de le refermer sur lui-même en un modèle sphérique ; toute densité plus faible qu'une certaine densité critique 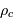 (univers parabolique) conduit à un modèle hyperbolique infini.
La détermination de la fonction de métrique
(univers parabolique) conduit à un modèle hyperbolique infini.
La détermination de la fonction de métrique 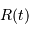 permet de décrire l'évolution de l'univers au cours du temps. L'application des équations d'Einstein à la métrique de Robertson-Walker conduit aux deux équations différentielles suivantes :
permet de décrire l'évolution de l'univers au cours du temps. L'application des équations d'Einstein à la métrique de Robertson-Walker conduit aux deux équations différentielles suivantes :
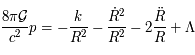
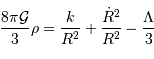
auxquelles on ajoute l'intégrale première:
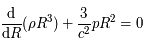
où 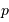 est la pression du fluide de galaxies,
est la pression du fluide de galaxies, 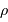 la densité de la matière, et
la densité de la matière, et 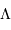 la constante cosmologique.
la constante cosmologique. 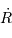 et
et 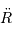 représentent respectivement les dérivées première et seconde du rayon de l'univers
représentent respectivement les dérivées première et seconde du rayon de l'univers 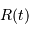 par rapport au temps.
On définit:
par rapport au temps.
On définit:
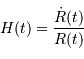 la constante de Hubble à
l'instant
la constante de Hubble à
l'instant 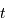 , i.e. le taux d'expansion à l'instant
, i.e. le taux d'expansion à l'instant 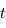 .
.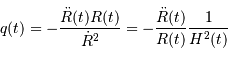 , le paramètre de décélération.
, le paramètre de décélération.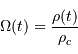 , le paramètre de densité.
, le paramètre de densité.
Si on suppose que l'univers est homogène et isotrope (principe
cosmologique), le modèle est entièrement défini par trois
paramètres : la valeur de la constante cosmologique
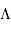 , la valeur actuelle de la constante de Hubble
, la valeur actuelle de la constante de Hubble 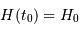 , et la valeur actuelle du paramètre de densité
, et la valeur actuelle du paramètre de densité 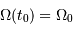 (ou du paramètre de décélération
actuel
(ou du paramètre de décélération
actuel 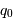 ). On considère généralement que la pression
). On considère généralement que la pression 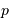 du fluide de galaxie est nulle, ce qui implique d'après les équations (1.1) et (1.2) que
du fluide de galaxie est nulle, ce qui implique d'après les équations (1.1) et (1.2) que 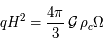 , et donc que
, et donc que 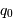 et
et 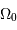 sont interchangeables.
sont interchangeables.
Dans les modèles de Friedman caractérisés par une constante cosmologique nulle (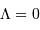 ), l'expansion se ralentit au cours du temps; il en résulte que l'âge
), l'expansion se ralentit au cours du temps; il en résulte que l'âge 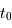 de l'Univers est toujours inférieur au temps de Hubble
de l'Univers est toujours inférieur au temps de Hubble 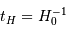 .
.