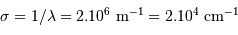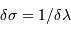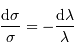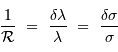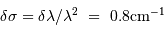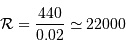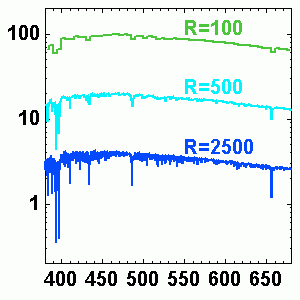
Spectre stellaire visible théorique à diverses résolutions spectrales
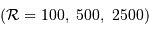
. La luminosité par intervalle spectral (unité arbitraire) est inversement proportionnelle à la résolution.
Crédit :
ASM
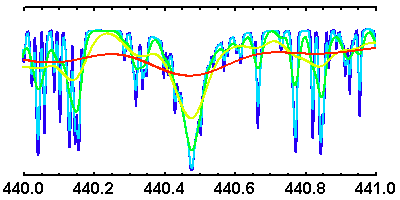
Échantillon d'un spectre stellaire observé à diverses résolutions spectrales
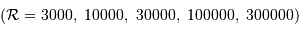
, avec renormalisation du flux.
Crédit :
ASM
Résolution spectrale
Plus la résolution d'un spectre stellaire théorique est élevée :
 Objectifs
Objectifs
Définir les notions de résolution spectrale : élément de résolution ; pouvoir de résolution ; intervalle spectral élémentaire.
Le pouvoir de résolution
Le pouvoir de résolution spectrale mesure la capacité à distinguer deux longueurs d'onde différentes 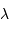 et
et 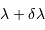 . Il est mesuré par la quantité :
. Il est mesuré par la quantité :
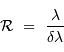
Le pouvoir de résolution est d'autant plus élevé que l'élément de résolution 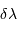 (également appelé résolution spectrale élémentaire ou élément spectral) est petit.
(également appelé résolution spectrale élémentaire ou élément spectral) est petit.
Conversions
Le pouvoir de résolution peut être exprimé avec les diverses grandeurs spectrales (longueur d'onde 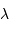 , fréquence
, fréquence 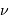 ) :
) :
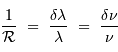
Il peut également être traduit en une vitesse, via l'équivalent Doppler:
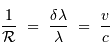
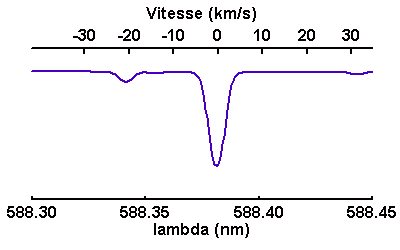
Raie stellaire représentée en fonction de la longueur d'onde ou de la vitesse repérée par rapport au centre de la raie.
Crédit :
ASM
Diverses résolutions
| Instrument | Pouvoir de résolution typique | 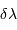 @ 500 nm (nm) @ 500 nm (nm) | vitesse (km/s) |
| Prisme | 500 | 1 | 600 |
| Réseau | 5000 | 0.1 | 60 |
| Réseau blazé | 50000 | 0.01 | 6 |
Le doublet du sodium
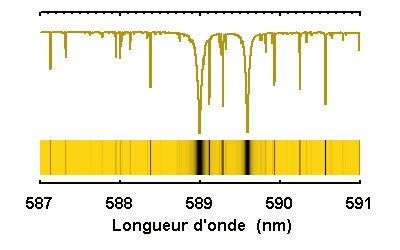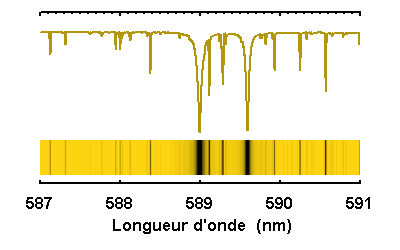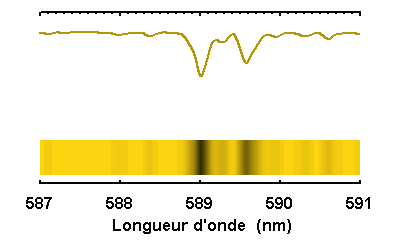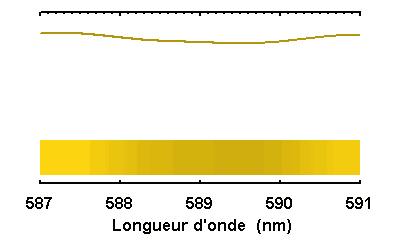
Le doublet jaune du sodium du spectre solaire,
simulé à diverses résolutions spectrales.
Crédit :
ASM
Résolution variable
Selon la résolution spectrale, des raies bien marquées, comme celles du sodium à 589.0 et 589.6 nm, apparaîtront plus ou moins clairement, avec l'identification de raies fines entre les 2 éléments du doublet, ou bien noyées dans le flux continu.
 Résolution et variable spectrale
Résolution et variable spectrale
Difficulté : ☆
Temps : 10 min
Un spectromètre assure un pouvoir de résolution 25 000 dans le visible à 500 nm.
Question 1)
Déterminer la largeur d'un élément spectral élémentaire.
 Quelle résolution ?
Quelle résolution ?
Difficulté : ☆
Temps : 20 min
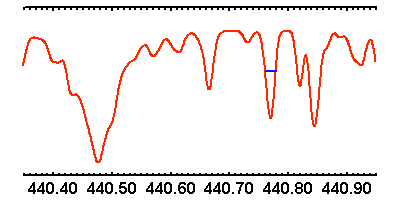
Le spectre ci-joint (voir l'appliquette) a été enregistré aux
alentours de 440.5 nm. Il s'agit d'estimer sa résolution, en fait
limitée par la résolution instrumentale.

Question 1)
Vaut-il mieux effectuer la mesure sur une raie fine ou une raie large ?
Réfléchir aux causes d'élargissement de la raie.
Question 2)
Estimer alors la résolution instrumentale
Estimer la largeur d'une raie à mi-hauteur

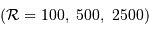 . La luminosité par intervalle spectral (unité arbitraire) est inversement proportionnelle à la résolution.
. La luminosité par intervalle spectral (unité arbitraire) est inversement proportionnelle à la résolution.

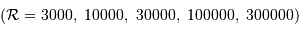 , avec renormalisation du flux.
, avec renormalisation du flux.
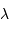 et
et 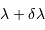 . Il est mesuré par la quantité :
. Il est mesuré par la quantité :
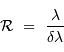
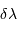 (également appelé résolution spectrale élémentaire ou élément spectral) est petit.
(également appelé résolution spectrale élémentaire ou élément spectral) est petit.
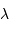 , fréquence
, fréquence 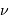 ) :
) :
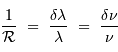
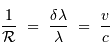

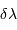 @ 500 nm (nm)
@ 500 nm (nm) 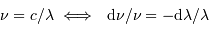 .
.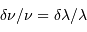 .
.
 . Exprimer le nombre d'onde
. Exprimer le nombre d'onde 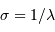 et la résolution
et la résolution 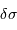 dans ce système d'unité.
dans ce système d'unité.
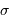 , c'est simple. Pour
, c'est simple. Pour 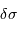 , il faut revenir à la définition.
, il faut revenir à la définition.
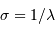 , calculer la différentielle
, calculer la différentielle 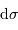 .
.

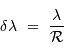
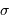 donne :
donne :