Apprendre

Objectifs

Définir les notions de résolution spectrale : élément de résolution ; pouvoir de résolution ; intervalle spectral élémentaire.

Le pouvoir de résolution

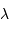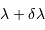Le pouvoir de résolution spectrale mesure la capacité à distinguer deux longueurs d'onde différentes $\lambda$ et $\lambda+\delta \lambda$ . Il est mesuré par la quantité :

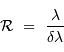
${\cal R} \ = \ {\lambda\over \delta\lambda}$

Le pouvoir de résolution est d'autant plus élevé que l'élément de résolution 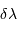$\delta\lambda$ (également appelé résolution spectrale élémentaire ou élément spectral) est petit.

Conversions

Le pouvoir de résolution peut être exprimé avec les diverses grandeurs spectrales (longueur d'onde 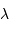$\lambda$ , fréquence $\nu$ ) :

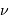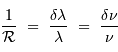
${1\over {\cal R}} \ = \ {\delta\lambda\over \lambda} \ = \ {\delta\nu\over \nu}$

Il peut également être traduit en une vitesse, via l'équivalent Doppler:

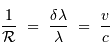
${1\over {\cal R}} \ = \ {\delta\lambda\over \lambda} \ = \ {v\over c}$

Diverses résolutions
Instrument	Pouvoir de résolution typique	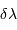$\delta\lambda$ @ 500 nm (nm)	vitesse (km/s)
Prisme	500	1	600
Réseau	5000	0.1	60
Réseau blazé	50000	0.01	6

Démonstration

La justification de ce qui précède procède en 2 étapes :

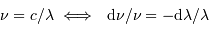Différentiation logarithmique : $\nu = c/\lambda \ \Longleftrightarrow\ \ {\mathrm{d}} \nu / \nu = - {\mathrm{d}}\lambda / \lambda$ .
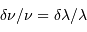Passage de la notation différentielle à une mesure : $\delta \nu / \nu = \delta\lambda / \lambda$ .