Le noyau : exercice 1

Les réactions nucléaires du noyau

La chaîne de réactions nucléaires menant de l'hydrogène à l'hélium est la suivante :

H¹ + H¹--> He²
He² --> H² + positon + neutrino (processus β+)
H² + H¹ --> He³ + photon
He³ + He³ --> Be⁶
Be⁶ --> He⁴ + H¹ + H¹(processus α)

Schématiquement, on considèrera que quatre atomes d'hydrogène se groupent pour former un atome d'hélium ₂He⁴(cette notation indique : 4 particules dans le noyau et 2 électrons autour). Nous allons par des considérations simples estimer la durée de vie du Soleil en supposant que la seule perte de masse se produit par rayonnement.

Données :

L'unité de masse atomique : 1,66 x10^-27 kg
Vitesse de la lumière : c =3 x 10⁸m.s^-¹
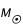Masse totale du Soleil : = 2 x 10³⁰ kg

Rappel : La masse atomique est la masse moyenne d’un atome. Elle prend en compte le nombre de particules constituant le noyau mais également la présence d’isotope (même nombre de protons et électrons mais nombre différent de neutrons) de cet élément dans la nature. Ainsi, l’hydrogène devrait avoir une masse atomique de 1 (1 proton dans le noyau). La présence en quantité non négligeable de deutérium (H² : 1 proton + 1 neutron) et de tritium (H³ : 1 proton, 2 neutrons) change cette masse pour 1,0079.

Question 1)

Si la masse atomique d'un atome d'hydrogène est de 1,0079, quelle est la masse atomique M_4H de 4 atomes d'hydrogène ?

Question 2)

La masse atomique M_He4de l'hélium ₂He⁴est 4,0026. Calculer la perte de masse ΔM entre le M_4H et M_He4en kg.

Question 3)

En utilisant la relation d'équivalence masse-énergie d'Einstein, E=mc² , déduire l'énergie libérée par cette perte de masse. Dans cette relation E est l'énergie libérée (exprimée en Joules, J), m est la masse transformée en énergie (exprimée en kg), et c est la vitesse de la lumière (exprimée en m/s).

Question 4)

Quelle est la fraction de masse d'hydrogène convertie en énergie ?

Question 5)

En considérant que seule 10% de la masse totale du Soleil 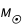M_soleil est susceptible de subir de telles réactions au cours de toute sa vie, déduire la quantité totale d’énergie 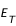E_T disponible. Pour cela, calculer d'abord la masse totale 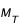M_T qui sera convertie puis appliquer la relation d'équivalence.

Question 6)

Sachant que le Soleil irradie 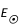E_soleil = 4.10²⁶ J/s, estimer le temps t nécessaire pour consommer tout l'hydrogène du cœur (donner le résultat en secondes puis en années). On supposera que l'énergie irradiée par le Soleil restera constante tout au long de sa vie.